图片.png
    这里要学一下回溯算法

    如果解决一个问题有多个步骤，每一个步骤有多种方法，题目又要我们找出所有的方法，可以使用回溯算法

    然后回到问题，组合问题（组合不考虑顺序，相似的那叫排列，考虑顺序），那举个🌰，直接用别人的图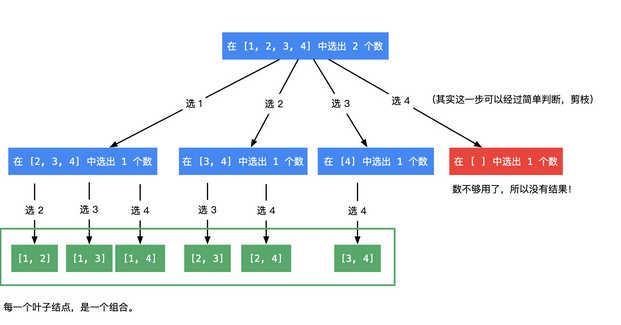
    图片.png
    注意这个剪枝
    理解下算法

    1. public class Solution {
    2.     public List<List<Integer>> combine(int n, int k) {
    3.         List<List<Integer>> res = new ArrayList<>();
    4.         if (k <= 0 || n < k) {
    5.             return res;
    6.         }
    7.         // 从 1 开始是题目的设定
    8.         Deque<Integer> path = new ArrayDeque<>();//双端队列
    9.         dfs(n, k, 1, path, res);
    10.         return res;
    11.     }
    12.     private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
    13.         // 递归终止条件是：path 的长度等于 k
    14.         if (path.size() == k) {
    15.             res.add(new ArrayList<>(path));
    16.             return;
    17.         }
    18.         // 遍历可能的搜索起点
    19.         for (int i = begin; i <= n; i++) {
    20.             // 向路径变量里添加一个数
    21.             path.addLast(i);
    22.             // 下一轮搜索，设置的搜索起点要加 1，因为组合数理不允许出现重复的元素
    23.             dfs(n, k, i + 1, path, res);
    24.             // 重点理解这里：深度优先遍历有回头的过程，因此递归之前做了什么，递归之后需要做相同操作的逆向操作
    25.             path.removeLast();
    26.         }
    27.     }
    28. }

    有点别的想法，但是还没实现，先放着