插入排序共分为：直接插入排序、二分法插入排序和希尔排序。


直接插入排序

例子：扑克牌的排序。 原理就是抽出每个元素找到合适的区间放置。

insertionSort.gif

  1. function insertionSort(arr) {
  2.     var len = arr.length;
  3.     var preIndex, current;
  4.     for (var i = 1; i < len; i++) {
  5.         preIndex = i - 1;
  6.         current = arr[i];
  7.         while(preIndex >= 0 && arr[preIndex] > current) {
  8.             arr[preIndex+1] = arr[preIndex];
  9.             preIndex--;
  10.         }
  11.         arr[preIndex+1] = current;
  12.     }
  13.     return arr;
  14. }

二分法插入排序（折半插入排序）

二分法只能用来查找，不能用来排序。而此处用到的二分就是快速找出要插入的位置。

概念：将数组的元素通过二分查找思想逐个插入到已排序的部分形成新的部分,当已排序数组的起始位置与原数组的起始位置一致时标志着排序结束。

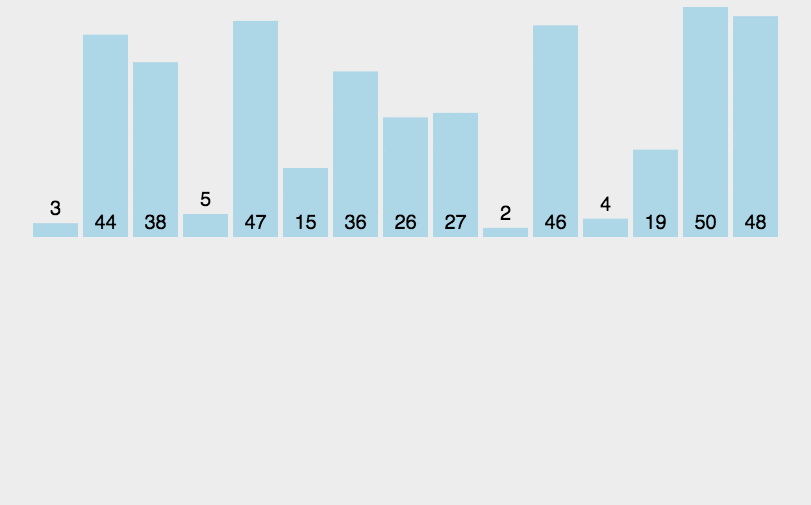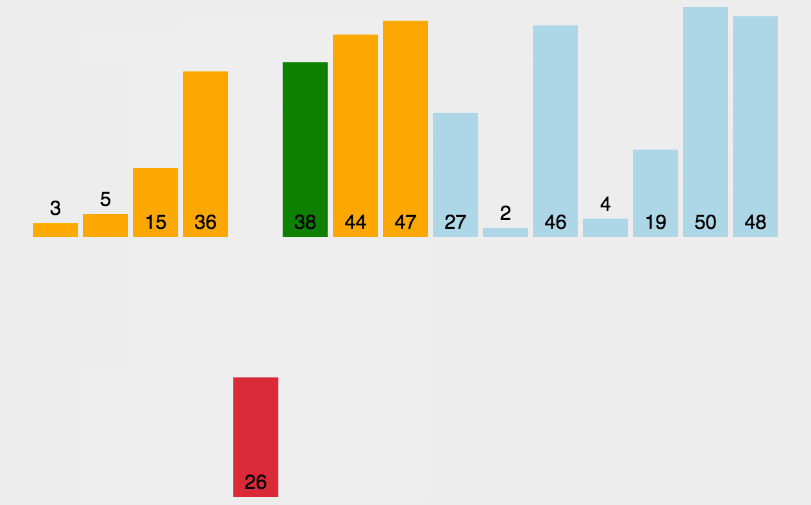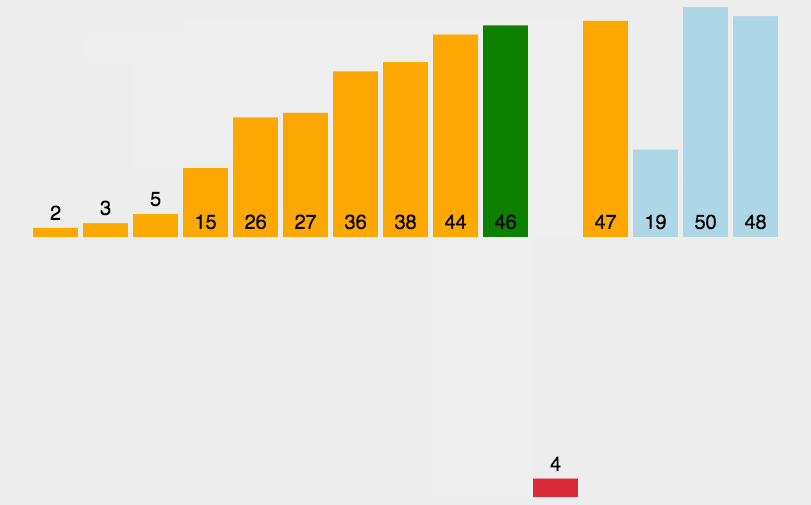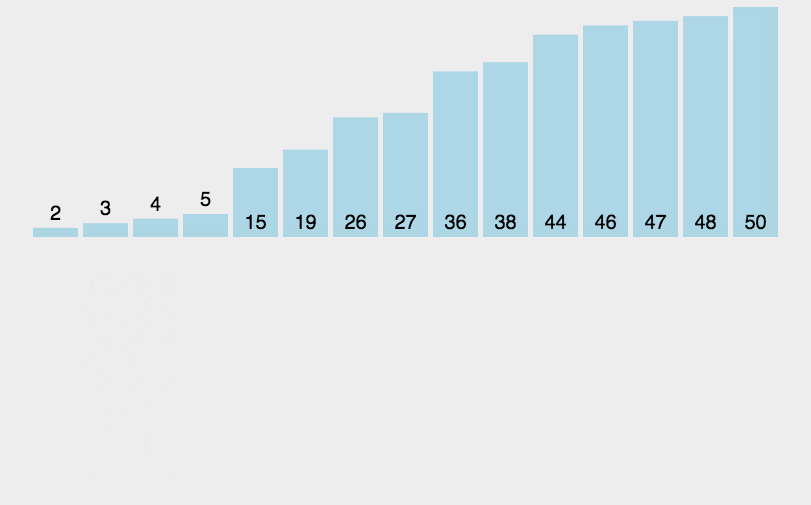
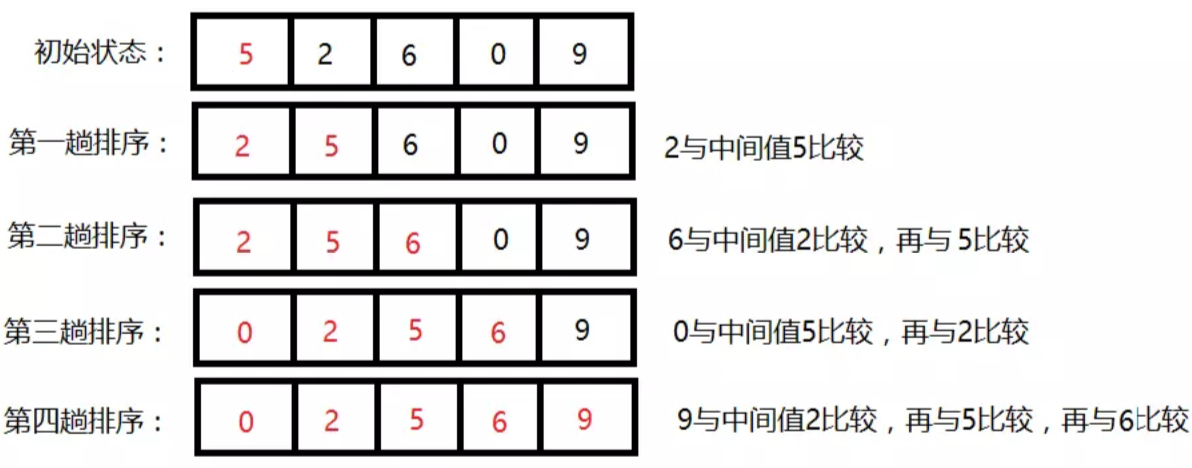
举个例子：下图的数组红色表示着已完成排序的数组，第一趟排序后，我们可以看出 arr[0~1] 的部分完成了排序，直到第四趟排序 arr[0~4] 与原数组的起始位置 [0~4]一致时，标志着所有元素完成了排序，排序结束。**

因此，我们需要记录完成排序的起始下标数。

a.png

  1. function binaryInsertSort(arr) {
  3.     //从第二个元素开始判断
  4.     for (let i = 1; i < arr.length; i++) {
  6.         //定义了插入区间起始位置和当前记录值
  7.         let leftIndex = 0, rightIndex = i - 1, recode = arr[i];
  9.         //说明此区间的元素超过2个，还需要查找区间
  10.         while (rightIndex - leftIndex > 1) {
  12.             //中间值的index，取整
  13.             let midIndex = parseInt((leftIndex + rightIndex) / 2);
  14.             //中间值
  15.             let midValue = arr[midIndex];
  17.             //判断与中间值的大小缩小查询区间
  18.             if (recode >= midValue) leftIndex = midIndex;
  19.             else rightIndex = midIndex;
  20.         }
  22.         arr.splice(i, 1);//删除该元素
  24.         //判断最后插入该值的左边还是右边
  25.         if (recode > arr[leftIndex]) arr.splice(leftIndex + 1, 0, recode);//右边
  26.         else arr.splice(leftIndex, 0, recode);//左边
  27.     }
  29.     return arr;
  30. }

希尔排序

希尔（shell）排序是对插入排序的优化 —— 插入排序在数据量小、有序程度高的情况下是高效的。而希尔排序则是保持了在数据量大、无序的情况下的高效性。

原理是将数据量拆为分若干个小的数据，再分别对他们进行插入排序。


对于希尔排序来说，增量是核心的判断条件。

步骤一：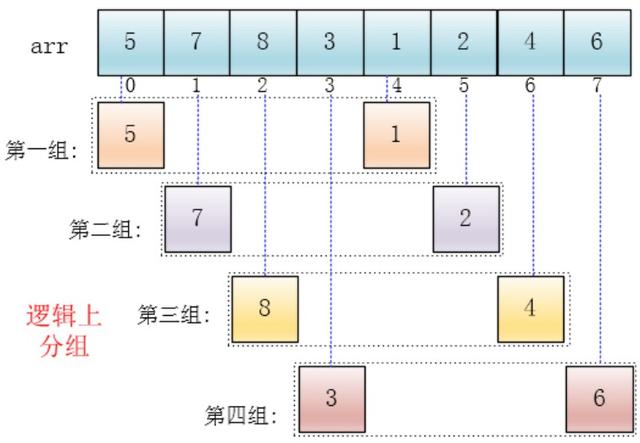
1523763390411731c4d486d.jpg
步骤二：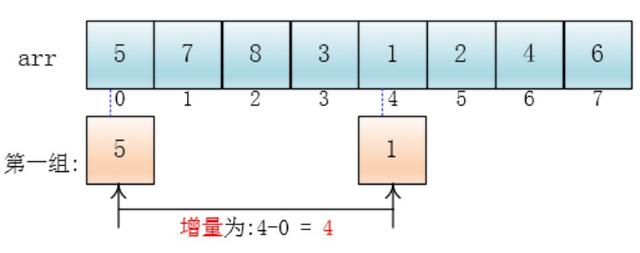
1523763390584d96604b701.jpg

步骤三：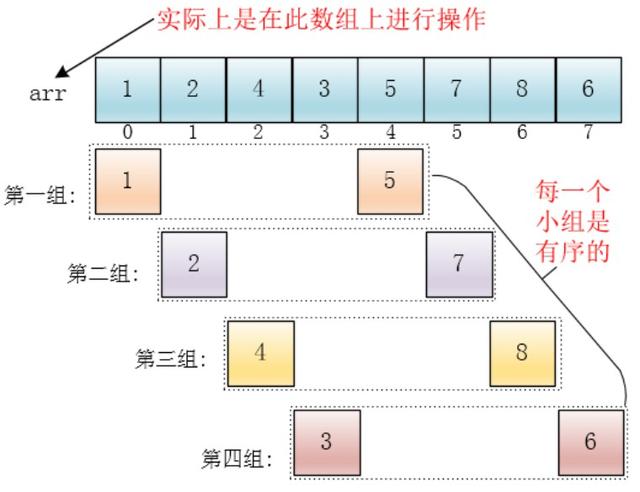
1523763390605f1acc654c8.jpg

排序后得到：[1,2,4,3,5,7,8,6]，这是第一次分组的结果，相对小的数在左侧，相对大的数在右侧。

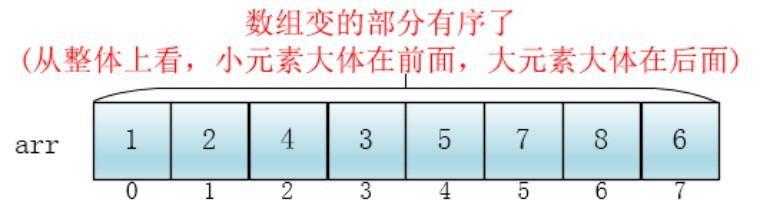
152376339063289c4f287a3.jpg

步骤四：增量缩小为上次的一半：2,

再次分组：

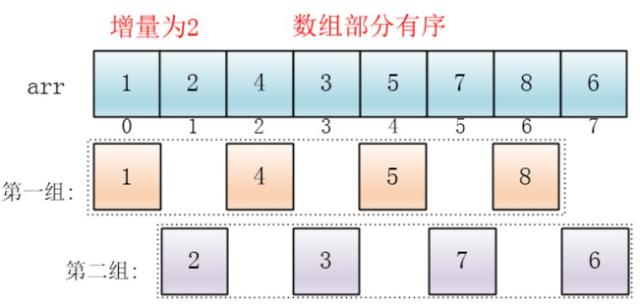
15237633906876d1db94cf9.jpg

然后对第一组、第二组分别插入排序，组成新的数组：

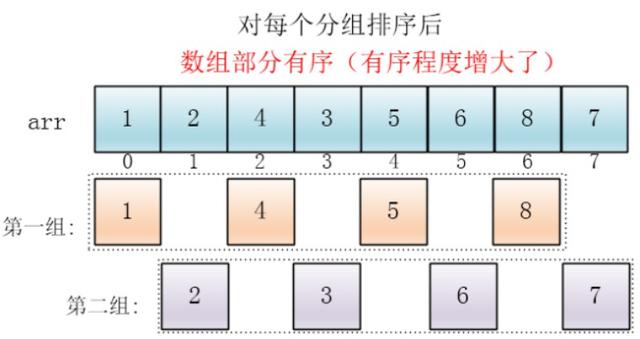
1523763390761f7f32df528.jpg

[1,2,4,3,5,6,8,7]

最后再次分组，增量为上次的一半：1（增量为1代表着最后一次分组，完成排序）

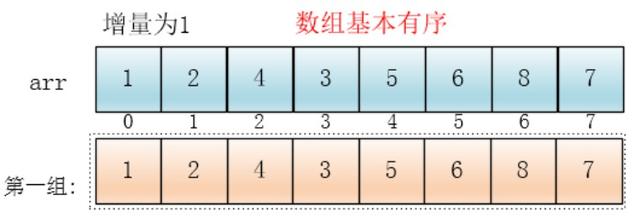
152376339087072702782c5.jpg

对唯一的一组插入排序：[1,2,3,4,5,6,7,8]
_
至此完成了排序，这种做法就是希尔排序，克服了大数据的无序的问题，使得插入排序效率得到非常大的提升。

以下是代码实现的过程：

基于上述的规律，增量最后必须为1，那么增量的选取应该是：2，1、2、4…（n为非负整数）。

对于任意长度 n 的数组 arr， 我们应该选取离 n/2 最近的 2，而这个初始增量的计算方式应该是：

(n/2)开2次方，四舍五入取整，得到一个 a，而距离最近的初始增量应该为2a，而分的组数量和增量是保持一致的。

  1. function binaryInsertSort(arr) {
  2.     for (var i = 1; i < arr.length; i++) {
  3.         var key = arr[i],
  4.             left = 0,
  5.             right = i - 1;
  6.         while (left <= right) {
  7.             var middle = parseInt((left + right) / 2);
  8.             if (key < arr[middle]) {
  9.                 right = middle - 1;
  10.             } else {
  11.                 left = middle + 1;
  12.             }
  13.         }
  14.         for (var j = i - 1; j >= left; j--) {
  15.             arr[j + 1] = arr[j];
  16.         }
  17.         arr[left] = key;
  18.     }
  19.     return arr;
  20. }
  22. function ShellSort(arr) {
  24.     let Len = arr.length;
  26.     let mi = Math.round(Math.sqrt(Len / 2))
  28.     let increment = Math.pow(2, mi);//初始增量
  30.     while (increment >= 1) {
  32.         for (let i = 0; i < increment; i++) {
  34.             //获取该组的下标和数据。
  35.             let index = [], data = [];
  36.             let sum = i;
  38.             while (sum < Len) {
  39.                 index.push(sum);
  40.                 data.push(arr[sum]);
  41.                 sum += increment;//增量
  42.             }
  44.                         //希尔排序的精髓之处：只对这个组进行直接插入排序，效率高。
  45.             data = binaryInsertSort(data);
  47.             for (let j = 0; j < index.length; j++) {
  48.                 arr[index[j]] = data[j];//将排序的数组应用到原数组中
  49.             }
  50.         }
  52.         increment = increment / 2;
  53.     }
  55.     return arr;
  56. }
  58. ShellSort([5, 7, 8, 3, 1, 2, 4, 6])