2. Bentley Rules for Optimizing Work

摘要

本节课讲述了 Bentley Rules，在四个方面减少工作量的主要方法

Work

什么是 Work ？

The work of a program (on a given input) is the sum total of all the operations executed by the program.

尽管 work 的减少不直接导致速度的增强，但往往是非常好的启发式设计 (do less, do faster)

Data structures

通过改变数据结构来减少工作量

Packing and encoding

打包，压缩和编码
以减少获取内存的次数和空间

Example 1. Encoding dates
String“September 11, 2018”需要 18-byte

• more than two double (64-bit) words

但实际上，考虑 在 4096 B.C.E. 和 4096 C.E. 之间的年份, 存在约 365.25 × 8192 ≈ 3 M 个日期
仅仅需要 ⎡lg(3×10^6)⎤ = 22 bits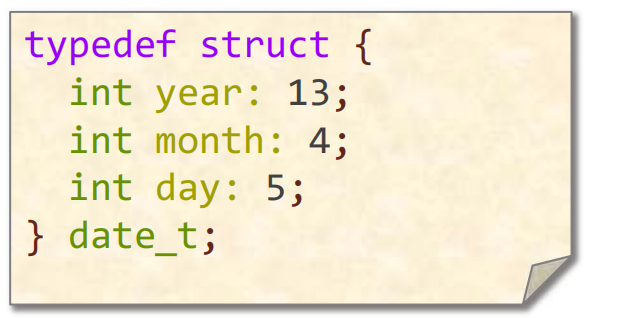

使用结构体，依旧使用22bit （但更加易读）
Tips: 可以指定类型所需的字段长度 int a: 3

注意：有时 unpacking and decoding 也是优化，取决于任务和数据解读的难度。

Augmentation

增强数据结构，以适应更多的任务

Example 2. Appending singly linked lists
为链表增加尾节点，使得 链表合并 的复杂度从 O(n) 下降到 O(1)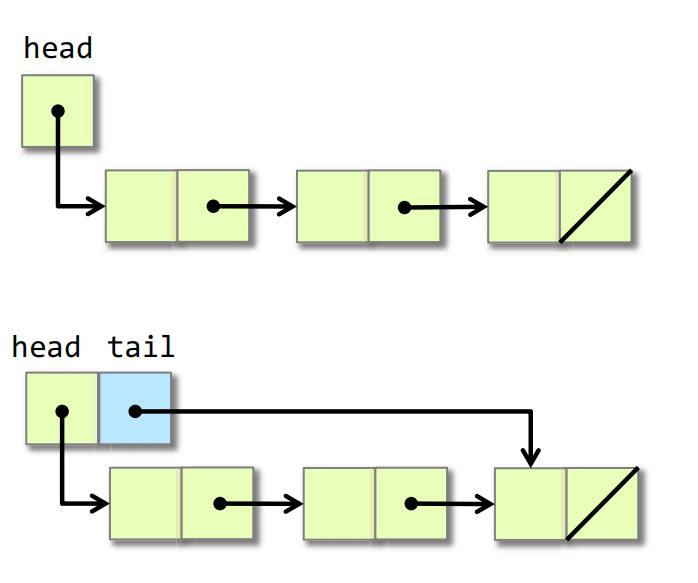

Precomputation

对于常用的数值进行预计算

Example 3. 组合数
可以提前将组合数 C(n，k) 计算得到并存储

Compile-Time Initialization

将计算工作在编译时进行，而非运行时

Example 4. 将计算得到的 组合数 C(n，k) 写在表内
如何生成这样的一张大表呢？使用元编程 (metaprogramming)

Cache

除了硬件实现的 Cache 之外，我们可以使用软件书写自己的 Cache

Example 5. 对于比较困难的计算，可以将计算过的结果存储在一个表内，对于已经计算过的结果，直接使用表内的 look up 即可

Sparsity

“The fastest way to compute is not to compute at all.”

Example 6. CSR format
对于熟悉图查询的各位应该比较熟悉，不再赘述

Logic

通过改变逻辑结构来实现加速

Constant Folding and Propagation

思想：通过替换和传播的方式计算常数表达式，一切都在编译时进行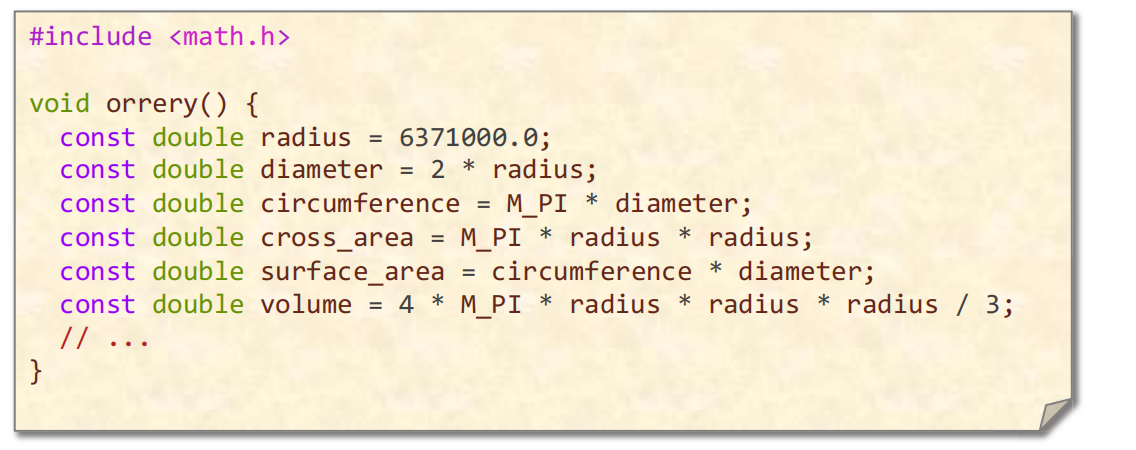

With a sufficiently high optimization level, all the expressions are evaluated at compile-time.

Common-Subexpression Elimination

思想：对于重复的计算式，只计算一次

当然，需要注意何时可以替换而何时不能

Algebraic Identities

利用数学恒等式来简化计算

Example. 平方计算以替代（代价更大的）sqrt() 函数

Short-Circuiting

思想：当结果已知时，即提前退出

Note that && and || are short-circuiting logical operators, and & and | are not

Order Testing

思想：基于短路的思想，将更常发生的情况前置

Example. 将更常见的空白符 空格 ‘ ‘ 和 换行符 ‘\n’ 前置

Creating a Fast Path

思想：使用简单的测试（放缩）， 一般来说，代价更小，准确率相对低

Example. Bloom Filter, 首先通过Bloom Filter（存在 false positive），再进入数据库进行精确查询

Combining Tests

思想：将一系列测试用一个测试或 switch 代替

Loops

Hoisting

思想：对于循环内的不变量，只计算一次

Sentinels

“哨兵” 思想
通过设置哨兵来减少循环判断的次数

Example. 检查数组中是否存在overflow
通常的做法需要两次判断

1. i < n
2. 当前是否 overflow

通过设置哨兵，在数组的最后一位添加 overflow，避免检查1
再通过对 i < n 的一次判断得出结果

Loop Unrolling

思想：展开循环
分为全展开(Full)和部分(Partial)展开
优势：

1. Lower number of instructions in loop control code 循环判断的次数更少
2. Enables more compiler optimizations 循环内的代码量变多，便于编译器优化的发挥

注意
Unrolling too much can cause poor use of instruction cache 过度的展开会导致 Cache 的效果降低

Loop Fusion

思想：对于具有相同的循环头 （index range）的循环，进行合并

Eliminating Wasted Iterations

和短路（short-circuiting）的思想相似，避免不必要的循环

Function

针对函数的优化

Inline

避免函数调用，以提升性能

Tail-Recursion Elimination

由于尾递归均可以写成迭代的形式，消除尾递归

Coarsening Recursion

思想：在递归算法中，提升 Base Case 的规模，用更有效的算法来处理他

Eg1. 在快排中，分段小于 Threshold 使用插入排序
Eg2. 在矩阵乘法中，分块小于 Threshold 使用 N^3 的朴素算法即可

总结

本节学习的 Bentley Rules 方法

Closing Advice

1. 避免过早优化。首先保证代码的正确性，然后逐步优化
2. Reducing Work 并不一定会减少时间，但是往往是好的方向 good heuristic
3. 编译器往往会自动进行许多优化
4. 当你需要知道编译器具体做了哪些优化时，查看编译代码 assembly code