二叉查找树

概念

二叉查找树是二叉树中最常用的一种类型，是为了实现快速查找的，不仅仅支持快速查找一个数，还支持快速插入和删除数据。二叉查找树的这些性能都依赖于二叉查找树的特殊结构，二叉查找树的要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都要大于这个节点的值。

查找

如果需要查找一个数，首先取根节点，如果它等于要查找的数据，则直接返回
如果小于要查找的数据，则在右子树中继续查找
如果大于要查找的数据，则在左子树中继续查找，也就是二分查找的思想，这样一直递归

插入

首先还是从根节点开始，然后依次比较要插入的数据与接地那的关系。
如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。
同理，如果要插入的数据比节点的数据小，也是类似的操作。

删除

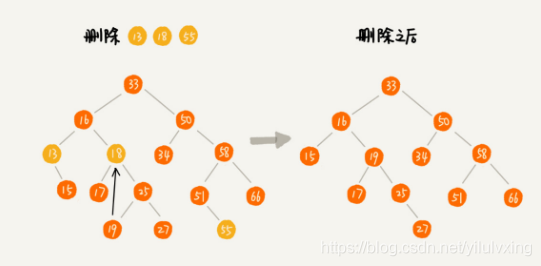
二叉查找树的删除相对于查找和插入要稍微复杂一点。主要有3种情况需要考虑：

• 如果要删除的节点没有子节点，只需要将父节点中，指向阐述接地那的指针置为NULL，比如删除图中的节点55
• 如果要删除的节点只有一个子节点（只有左子节点或者右子节点），只需要删除父节点中，指向要删除的指针，让它指向要删除的节点的子节点就可以了。比如要删除图中节点13
• 如果要删除的节点上有两个子节点，要稍微复杂一点。首先找到这个节点的右子树中最小的节点，把它替换到要删除的节点，然后再删除这个最小节点。因为最小节点肯定没有左子节点

  时间复杂度

二叉查找树的总结

二叉查找树，除了插入、删除、查找之外，还可以支持快速查找最大节点、最小节点、前继节点、后继节点。同事二叉查找树还有一个重要特性，就是 中序遍历二叉树，可以输出有序的数据序列，时间复杂度为O（n），非常高效。

进一步思考： 二叉查找树可以支持快速插入、删除、查找操作，各个操作的时间复杂度与树的高度成正比，最理想情况下，时间复杂度是O(logn)。

但在极端情况下，比如频繁的删除等操作，二叉树会退化成一个链表，那么时间复杂度就变成了O(n)。

因此，为了避免这种极端情况，后来又设计一种平衡二叉树，平衡二叉查找树的高度接近 logn，所以插入、删除、查找操作的时间复杂度也比较稳定，是 O(logn）。