基于支持向量机（SVM）的分类预测

[Data Whale - 2020年8月组队打卡任务 - by Golden (wechat: freealafeimax)]

1. 前言

支持向量机（Support Vector Machine，SVM）是一个非常优雅的算法，具有非常完善的数学理论，常用于数据分类，也可以用于数据的回归预测中，由于其优美的**理论保证和利用核函数对于线性不可分问题的处理技巧**， 在上世纪90年代左右，SVM曾红极一时。 本文将不涉及非常严格和复杂的理论知识，力求于通过直觉来感受 SVM。

2. 学习目标

  • 了解SVM的分类标准
  • 了解SVM的软间隔分类
  • 了解SVM的非线性核函数分类

[阿里云notebook：https://developer.aliyun.com/ai/scenario/b6c1ef3172d84236ae10c3b91798a796]

3. 代码流程

Demo实践

  • Step1:库函数导入
  • Step2:构建数据集并进行模型训练
  • Step3:模型参数查看
  • Step4:模型预测
  • Step5:模型可视化

4. 算法实战

4.1 Demo实践

首先我们利用sklearn直接调用 SVM函数进行实践尝试

Step1: 库函数导入

  1. ## 基础函数库
  2. import numpy as np
  4. ## 导入画图库
  5. import matplotlib.pyplot as plt
  6. import seaborn as sns
  8. ## 导入逻辑回归模型函数
  9. from sklearn import svm

Step2: 构建数据集并进行模型训练

  1. ## Demo演示SVM分类
  2. ## 构造数据集
  3. x_features = np.array([[-1,-2],[-2,-1],[-3,-2],[1,3],[2,1],[3,2]])
  4. y_label = np.array([0,0,0,1,1,1])
  6. ## 调用SVC模型（支持向量机分类）
  7. svc = svm.SVC(kernel = 'linear')
  9. ## 用SVM模型拟合构造的数据集
  10. svc = svc.fit(x_features, y_label)

Step3: 模型参数查看

  1. ## 查看其对应模型的w
  2. print('the weight of SVM:', svc.coef_)
  4. ## 查看其对应模型的w0
  5. print('the intercept(w0) of SVM:', svc.intercept_)

Ouput:
image.png
截距 intercept w0只有一个
由于有2个特征变量，所以会有2个权重参数for x1, x2

Step4: 模型预测

  1. y_train_pred = svc.predict(x_features)
  2. print('The prediction result:',y_train_pred)

Output:
The prediction result: [0 0 0 1 1 1]

Step5: 模型可视化

由于此处选择的线性核函数，所以在此我们可以将svm进行可视化。

  1. # 最佳函数
  2. x_range = np.linspace(-3,3)
  3. w = svc.coef_[0]
  4. a = -w[0] / w[1]
  5. y_3 = a*x_range - (svc.intercept_[0] / w[1])
  7. # 可视化决策边界
  8. plt.figure()
  9. plt.scatter(x_features[:,0], x_features[:,1], c=y_label, s=50, cmap='viridis')
  10. plt.plot(x_range, y_3, '-c')
  11. plt.show()

Output: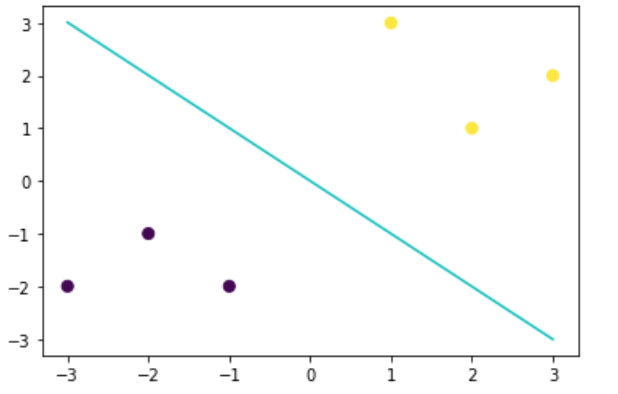
image.png
可以对照之前的逻辑回归模型的决策边界，我们可以发现两个决策边界是有一定差异的（可以对比2者在X,Y轴上的截距）， 这说明这2个不同在相同数据集 上找到的判别线是不同的，而这不同的原因其实是由于两者选择的 最优目标 是不一致的。接下来我们进行SVM的一些简单介绍。

===> 延伸阅读
np.linspace()

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
产生从start到stop的等差数列，num为元素个数，默认50个
多用于模型训练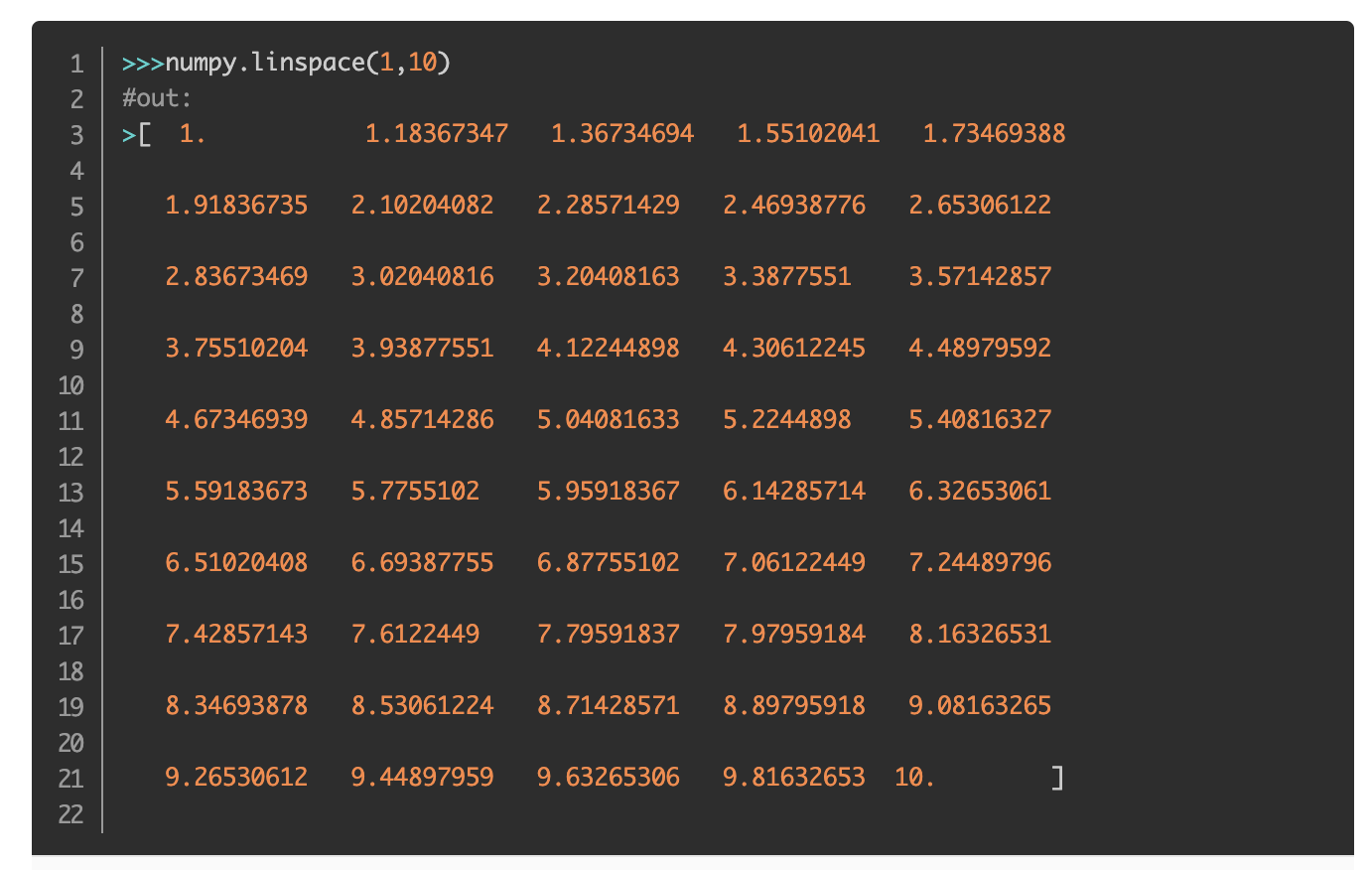
image.png
可见，这里我们生成了从 -3 到3 的等差数列。原因是因为我们用的是线性核函数。

5. 支持向量机SVM介绍

我们常常会碰到这样的一个问题，首先给你一些分属于两个类别的数据

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from sklearn.datasets.samples_generator import make_blobs
  4. %matplotlib inline
  6. # 画图
  7. X,y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  8. plt.scatter(X[:,0],X[:,1],c=y,s=60,cmap=plt.cm.Paired)

Output: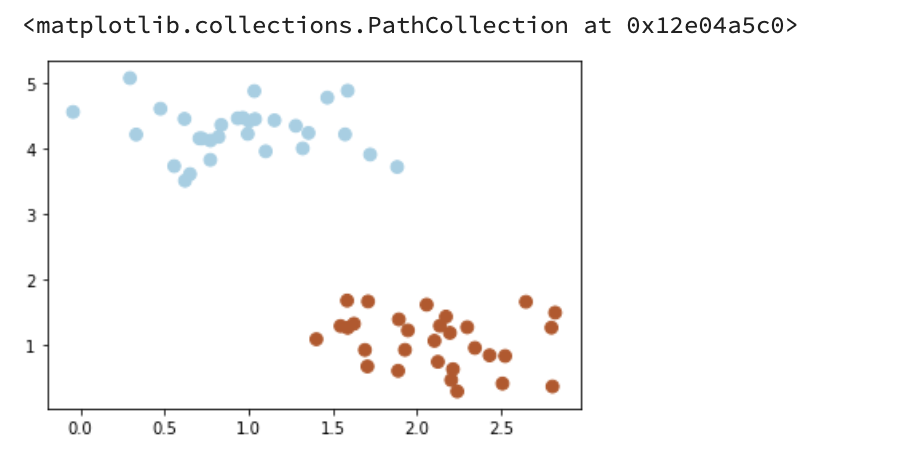
image.png
现在需要一个线性分类器，将这些数据分开来。
我们可能会有多重分法：

  1.  画散点图
  2. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  3. plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap=plt.cm.Paired)
  4. x_fit = np.linspace(0,3)
  6. # 画函数
  7. y_1 = 1 * x_fit + 0.8
  8. plt.plot(x_fit, y_1, '-c')  # green line
  9. y_2 = -0.3 * x_fit +3
  10. plt.plot(x_fit, y_2, '-k')  # black line

Output: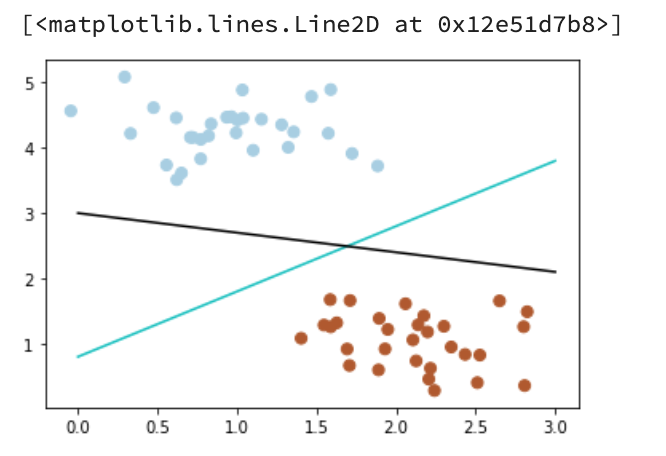
image.png

那么现在有一个问题，2个分类器，哪一个更好呢？
为了判断好坏，我们需要引入一个准则：好的分类器不仅仅是能够很好的分开已有的数据集，还能对未知数据集 进行2个的划分。
假设，现在有一个属于红色数据点的新数据（3，2.8）

  1. # 画散点图
  2. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  3. plt.scatter(X[:,0], X[:,1], c=y, s=50, cmap=plt.cm.Paired)
  4. plt.scatter([3],[2.8],c='#cccc00',marker='<',s=100,cmap=plt.cm.Paired)  # new point: 黄色的点
  5. x_fit = np.linspace(0,3)
  7. # 画函数
  8. y_1 = 1*x_fit + 0.8
  9. plt.plot(x_fit,y_1,'-c')
  10. y_2 = -0.3*x_fit +3
  11. plt.plot(x_fit,y_2,'-k')

Output: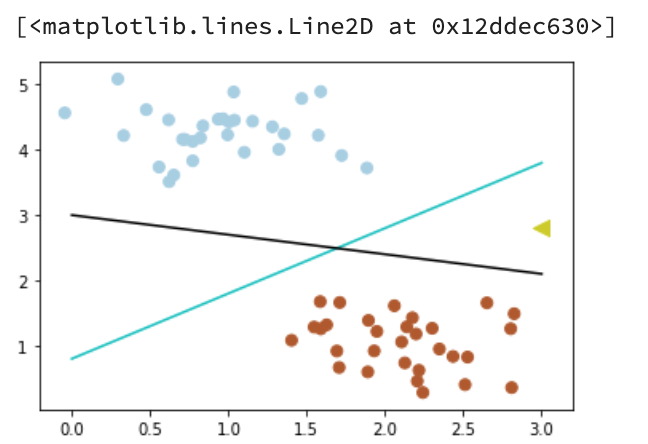
image.png
可以看到，此时黑色的线会把这个新的数据集分错，而蓝色的线不会。
我们刚刚举的例子可能会带有一些主观性。

===>延伸阅读

plt.cm中cm全称表示colormap，

paired表示两个相近色彩输出，比如浅蓝、深蓝**；浅红、深红；浅绿，深绿**这种。

参数c就是color

<===

那么如何客观地评价两条线的健壮性呢？
此时，我们需要引入一个非常重要的概念：最大间隔。
最大间隔刻画着当前分类器与数据集的边界
以这2个分类器为例：

  1. # 画散点图
  2. X,y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  3. plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap=plt.cm.Paired)
  4. x_fit = np.linspace(0,3)
  6. # 画函数
  7. y_1 = 1*x_fit + 0.8
  8. plt.plot(x_fit,y_1,'-c')
  10. # 画边距
  11. plt.fill_between(x_fit,y_1-0.6, y_1+0.6,edgecolor='none',color='#AAAAAA',alpha=0.4)
  12. y_2 = -0.3*x_fit +3
  13. plt.plot(x_fit,y_2,'-k')
  14. plt.fill_between(x_fit, y_2 - 0.4, y_2+0.4,edgecolor='none',color='#AAAAAA',alpha=0.4)

Output: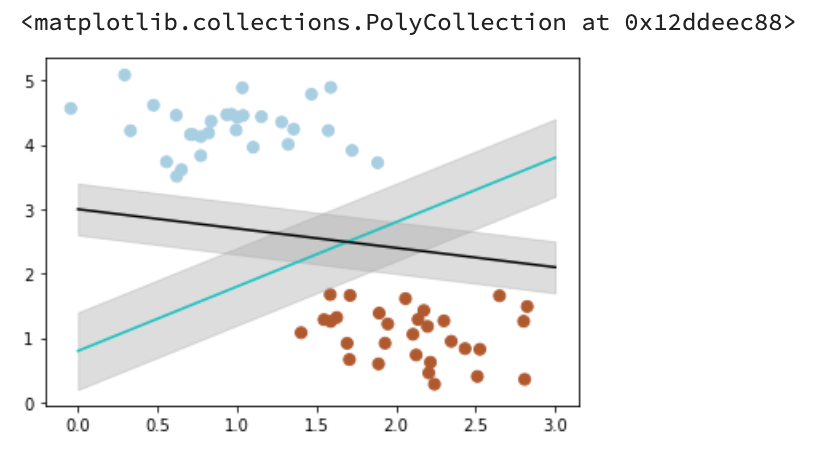
image.png
可以看到，蓝色的线最大间隔是大于黑色的线的。
所以我们会选择蓝色的线作为我们的分类器。

  1. # 画散点图
  2. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  3. plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap=plt.cm.Paired)
  5. # 画图
  6. y_1 = 1*x_fit + 0.8
  7. plt.plot(x_fit,y_1,'-c')
  9. # 画边距
  10. plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA',alpha=0.4)

Output: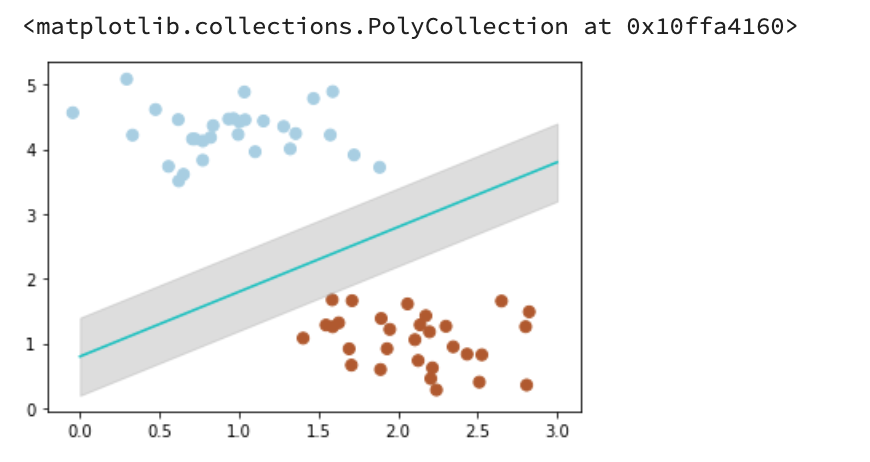
image.png
那么，我们现在的分类器是最优分类器吗？
或者说，有没有更好的分类器，它具有更大的间隔？
答案是有的。
为了找出__最优分类器，我们需要引入我们今天的主角：SVM

  1. from sklearn.svm import SVC
  3. # SVM 函数
  4. clf = SVC(kernel='linear')
  5. clf.fit(X,y)

Output:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=’ovr’, degree=3, gamma=’auto_deprecated’,
kernel=’linear’, max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)

  1. # 最佳函数
  2. w = clf.coef_[0]
  3. a = -w[0]/w[1]
  4. y_3 = a*x_fit - (clf.intercept_[0])/w[1]
  6. # 最大边距 下届
  7. b_down = clf.support_vectors_[0]
  8. y_down = a*x_fit + b_down[1] - a * b_down[0]
  10. # 最大边距 上届
  11. b_up = clf.support_vectors_[-1]
  12. y_up = a*x_fit + b_up[1] - a*b_up[0]
  1. # 画散点图
  2. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  3. plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap=plt.cm.Paired)
  5. # 画函数
  6. plt.plot(x_fit, y_3, '-c')
  8. # 画边距
  9. plt.fill_between(x_fit, y_down, y_up, edgecolor='none',color='#AAAAAA',alpha=0.4)
  11. # 画支持向量
  12. plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],edgecolor='b',s=80,facecolors='none')

Output: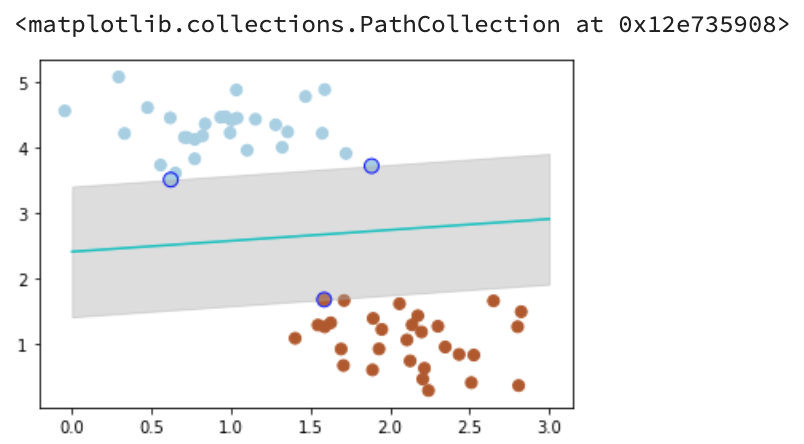
image.png
带蓝边的二点是距离当前分类器最近的点，我们称之为支持向量。
支持向量机为我们提供了在众多可能的分类器之间进行选择的原则，从而确保对未知数据集具有更高的泛化性。

但在很多时候，我们拿到的数据是这样子的：

  1. # 画散点图
  2. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
  3. plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap=plt.cm.Paired)

Output: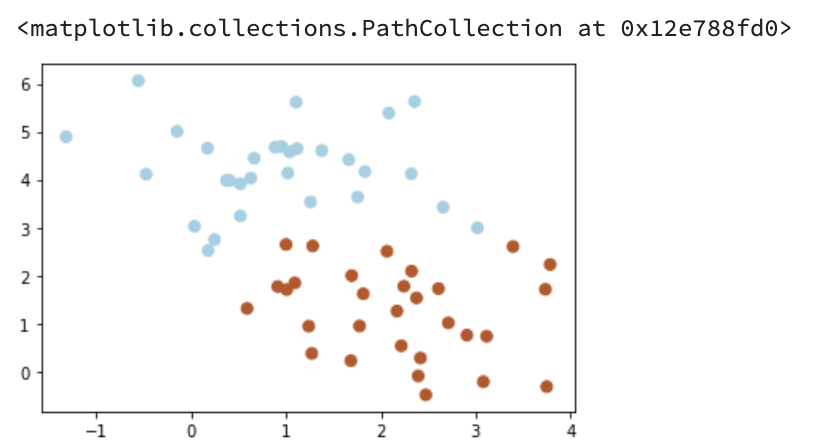
image.png
这种情况并不容易找到这样的最大间隔。
于是我们就有了软间隔**，相比于硬间隔而言，我们允许个别数据出现在间隔带中。
我们知道，如果没有一个原则进行约束，满足软间隔的分类器也会出现很多条。
所以需要对分错的数据进行乘法，SVC函数中，有一个参数C就是乘法参数。
乘法参数越小，容忍性就越大。(即C=0.2 比C=1 容忍性大)**
以C=1为例：

  1. # 画散点图
  2. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
  3. plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
  5. # 惩罚参数：C=1
  6. clf = SVC(C=1, kernel='linear')
  7. clf.fit(X, y)
  9. # 最佳函数
  10. w = clf.coef_[0]
  11. a = -w[0] / w[1]
  12. y_3 = a*x_fit - (clf.intercept_[0]) / w[1]
  14. # 最大边距 下届
  15. b_down = clf.support_vectors_[0]
  16. y_down = a* x_fit + b_down[1] - a * b_down[0]
  18. # 最大边距 上届
  19. b_up = clf.support_vectors_[-1]
  20. y_up = a* x_fit + b_up[1] - a * b_up[0]
  22. # 画散点图
  23. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  24. plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
  26. # 画函数
  27. plt.plot(x_fit, y_3, '-c')
  29. # 画边距
  30. plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
  32. # 画支持向量
  33. plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
  34.  s=80, facecolors='none')

Output: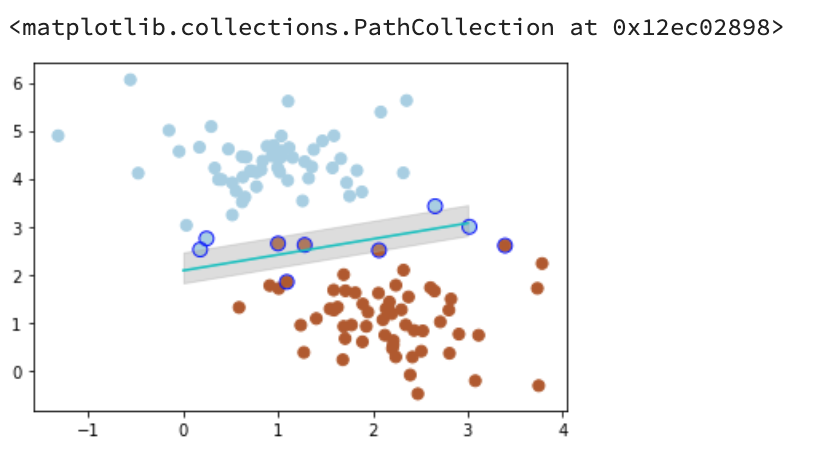
image.png
惩罚参数C=0.2时，SVM会更具包容性，从而兼容更多的错分样本。

  1. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
  2. plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
  4. # 惩罚参数：C=0.2
  5. clf = SVC(C=0.2, kernel='linear')
  6. clf.fit(X, y)
  7. x_fit = np.linspace(-1.5, 4)
  9. # 最佳函数
  10. w = clf.coef_[0]
  11. a = -w[0] / w[1]
  12. y_3 = a*x_fit - (clf.intercept_[0]) / w[1]
  14. # 最大边距 下届
  15. b_down = clf.support_vectors_[10]
  16. y_down = a* x_fit + b_down[1] - a * b_down[0]
  18. # 最大边距 上届
  19. b_up = clf.support_vectors_[1]
  20. y_up = a* x_fit + b_up[1] - a * b_up[0]
  22. # 画散点图
  23. X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
  24. plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
  26. # 画函数
  27. plt.plot(x_fit, y_3, '-c')
  29. # 画边距
  30. plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
  32. # 画支持向量
  33. plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
  34.  s=80, facecolors='none')

Output: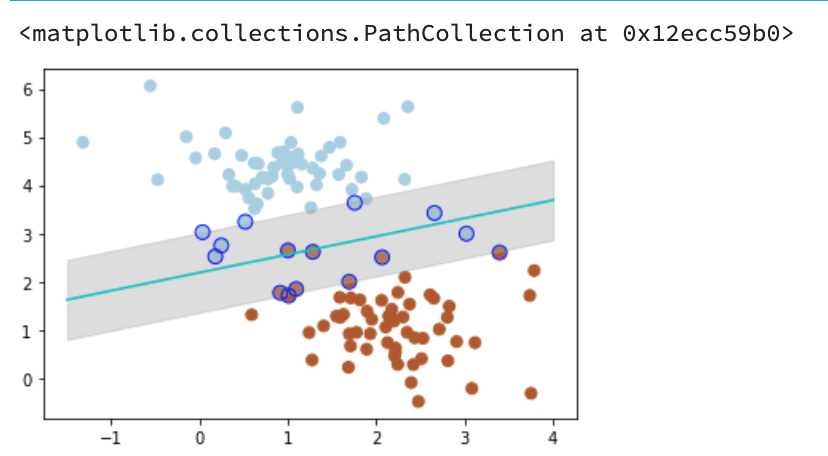
image.png
===>延伸阅读
color=’#AAAAAA’ 灰色
image.png
<===

如果我们遇到这样的数据集，没有办法利用线性分类器进行分类：

  1. from sklearn.datasets.samples_generator import make_circles
  2. # 画散点图
  3. X, y = make_circles(100, factor=0.1, noise=0.1, random_state=2019)
  4. plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap=plt.cm.Paired)
  5. clf = SVC(kernel='linear').fit(X,y)
  7. # 最佳函数
  8. x_fit = np.linspace(-1.5,1.5) 
  9. w = clf.coef_[0]
  10. a = -w[0]/w[1]
  11. y_3 = a*X - (clf.intercept_[0])/w[1]
  12. plt.plot(X, y_3, '-c')

Output: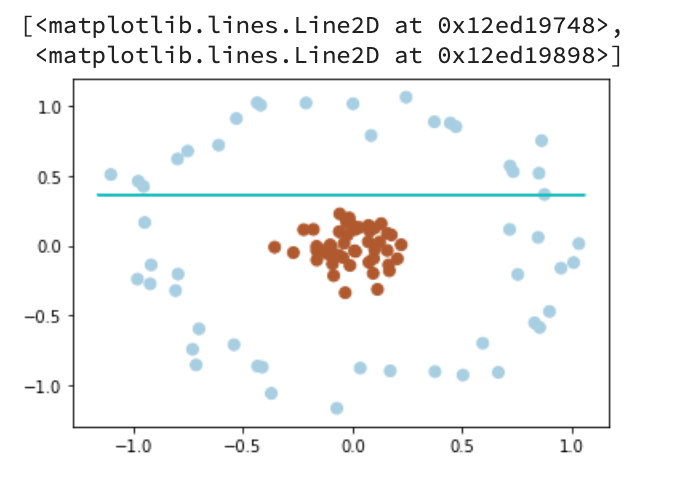
image.png
我们可以将二维（低维）空间的数据映射到三维（高维）空间中。
此时，我们便可以通过一个超平面对数据进行划分。
所以，我们映射的目的在于使用 SVM 在高维空间找到超平面的能力。

  1. from mpl_toolkits.mplot3d import Axes3D
  3. # 数据映射
  4. r = np.exp(-(X[:, 0] ** 2 + X[:, 1] ** 2))
  5. ax = plt.subplot(projection='3d')
  6. ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap=plt.cm.Paired)
  7. ax.set_xlabel('x')
  8. ax.set_ylabel('y')
  9. ax.set_zlabel('z')
  10. x_1, y_1 = np.meshgrid(np.linspace(-1, 1), np.linspace(-1, 1))
  11. z = 0.01*x_1 + 0.01*y_1 + 0.5
  12. ax.plot_surface(x_1, y_1, z, alpha=0.3)

Output: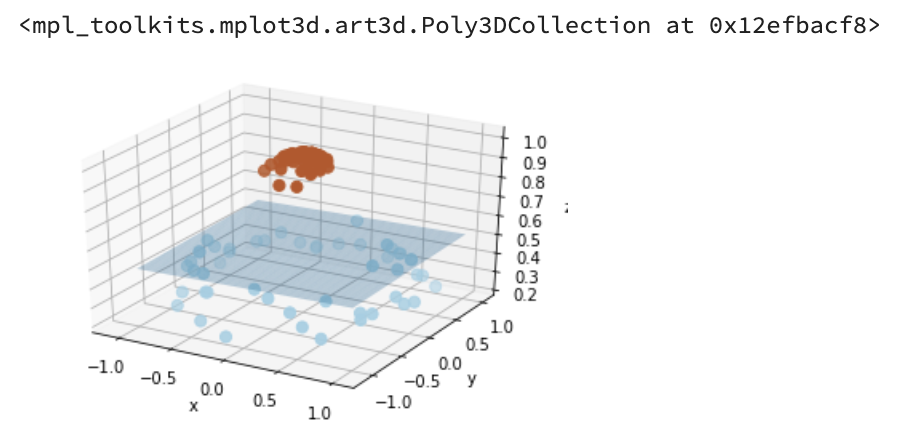
image.png
在 SVC 中，我们可以用高斯核函数来实现这以功能：kernel=’rbf’

  1. # 画图
  2. X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
  3. plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
  4. clf = SVC(kernel='rbf')
  5. clf.fit(X, y)
  6. ax = plt.gca()
  7. x = np.linspace(-1, 1)
  8. y = np.linspace(-1, 1)
  9. x_1, y_1 = np.meshgrid(x, y)
  10. P = np.zeros_like(x_1)
  11. for i, xi in enumerate(x):
  12.     for j, yj in enumerate(y):
  13.         P[i, j] = clf.decision_function(np.array([[xi, yj]]))
  14. ax.contour(x_1, y_1, P, colors='k', levels=[-1, 0, 0.9], alpha=0.5,
  15.  linestyles=['--', '-', '--'])
  16. plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
  17.  s=80, facecolors='none');

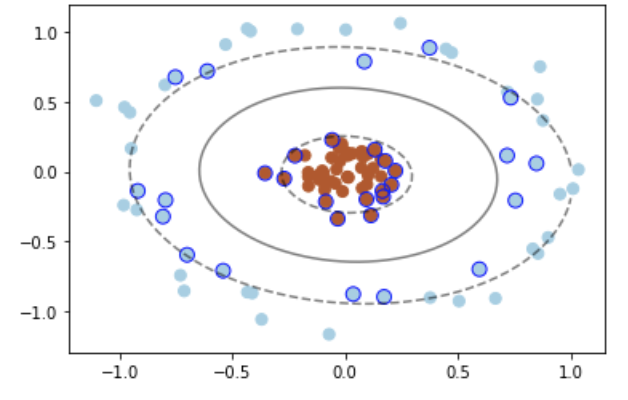
image.png
此时便完成了非线性分类。
SVM 的基础知识的直观感受到此就结束了。