java-递归 - 《Java 基础学习》

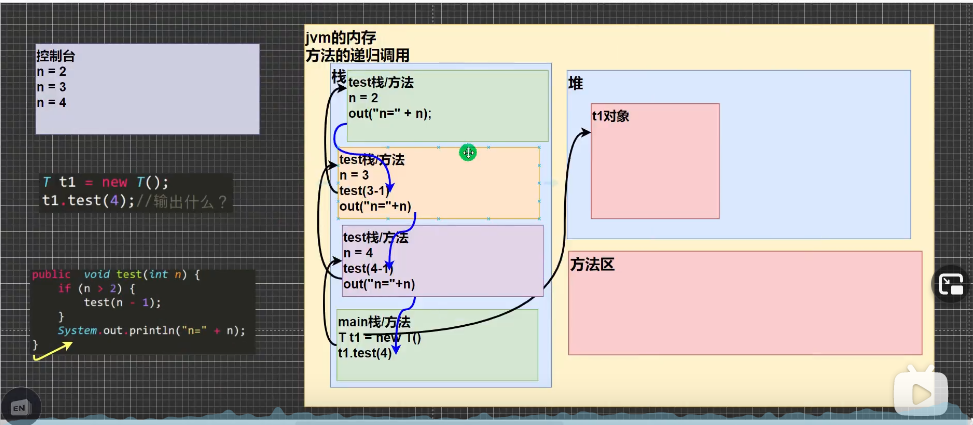
在哪里调用就返回那里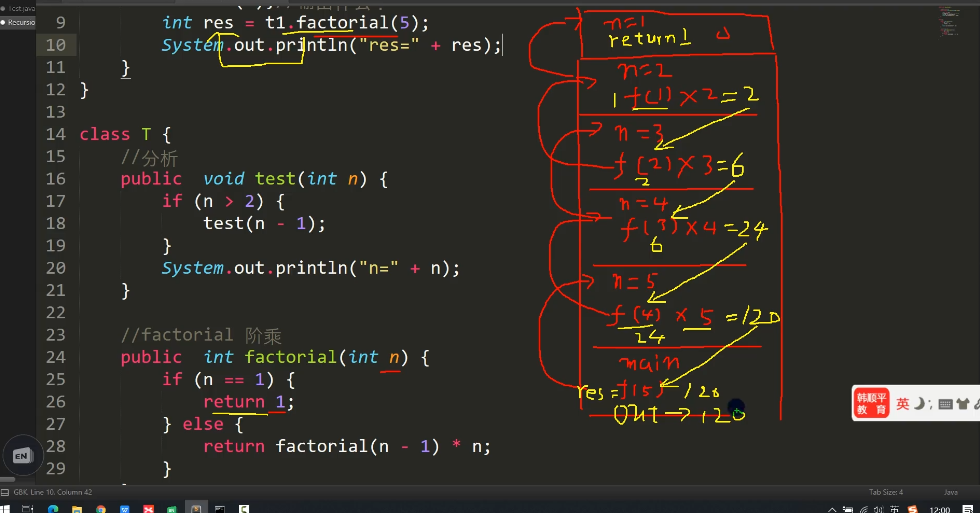


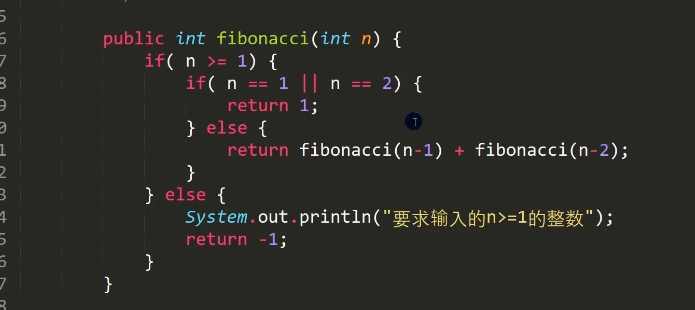
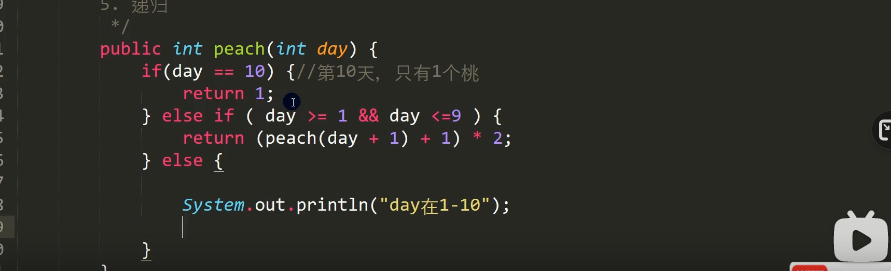
public class RecursionExercise01 { 
    //编写一个main方法
    public static void main(String[] args) {
        T t1 = new T();
        // int n = 7;
        // int res = t1.fibonacci(n);
        // if(res != -1) {
        //     System.out.println("当n="+ n +" 对应的斐波那契数=" + res);
        // } 
        // 
        //桃子问题
        int day = 0;
        int peachNum = t1.peach(day);
        if(peachNum != -1) {
            System.out.println("第 " + day + "天有" + peachNum + "个桃子");
        }
    }
}
class T {
        /*
        请使用递归的方式求出斐波那契数1,1,2,3,5,8,13...给你一个整数n，求出它的值是多
        思路分析
        1. 当n = 1 斐波那契数 是1
        2. 当n = 2 斐波那契数 是1
        3. 当n >= 3  斐波那契数 是前两个数的和
        4. 这里就是一个递归的思路
         */
        public int fibonacci(int n) {
            if( n >= 1) {
                if( n == 1 || n == 2) {
                    return 1;
                } else {
                    return fibonacci(n-1) + fibonacci(n-2);
                }
            } else {
                System.out.println("要求输入的n>=1的整数");
                return -1;
            }
        }
        /*
        猴子吃桃子问题：有一堆桃子，猴子第一天吃了其中的一半，并再多吃了一个！
        以后每天猴子都吃其中的一半，然后再多吃一个。当到第10天时，
        想再吃时（即还没吃），发现只有1个桃子了。问题：最初共多少个桃子？
        思路分析 逆推
        1. day = 10 时 有 1个桃子
        2. day = 9 时  有 (day10 + 1) * 2 = 4
        3. day = 8 时  有 (day9 + 1) * 2 = 10
        4. 规律就是  前一天的桃子 = (后一天的桃子 + 1) *2//就是我们的能力
        5. 递归
         */
        public int peach(int day) { 
            if(day == 10) {//第10天，只有1个桃
                return 1; 
            } else if ( day >= 1 && day <=9 ) {
                return (peach(day + 1) + 1) * 2;//规则，自己要想
            } else {
                System.out.println("day在1-10");
                return -1;
            }
        }
}

斐波那契

public class RecursionExercise02 {
    public static void main(String[] args){
        T t1 = new T();
        System.out.println(t1.hahah(6));
    }
}
class T{
    /*
    请使用递归的方式求出斐波那契数 1,1,2,3,5,8,13...给你一个整数 n， 求出它的值是多
    思路分析
    1. 当 n = 1 斐波那契数 是 1
    2. 当 n = 2 斐波那契数 是 1
    3. 当 n >= 3 斐波那契数 是前两个数的和
    4. 这里就是一个递归的思路
    */
    public int hahah(int n){
        if(n >= 1){
            if(n == 1 || n == 2){
            return 1;
            }else {
                return hahah(n - 1) +hahah(n - 2);
            }
        }else{
            System.out.println("请输入大于1的正整数");
            return -1;
        }
    }
}

猴子吃桃问题

public class RecursionExercise01 { 
    //编写一个main方法
    public static void main(String[] args) {
        T p1 = new T();
         System.out.println(p1.peach(9)) ;
    }
}
class T{
    /*
    猴子吃桃子问题： 有一堆桃子， 猴子第一天吃了其中的一半， 并再多吃了一个！
    以后每天猴子都吃其中的一半， 然后再多吃一个。 当到第 10 天时，
    想再吃时（即还没吃） ， 发现只有 1 个桃子了。 问题： 最初共多少个桃子？
    第10天剩下一个 第九天 4个  吃了一半 2+1=3 正好剩下一个
    10  1 个
    9   (10天+1)*2   (1+1)*2=4
    8    (9天+1)*2   (4+1)*2=10
    7    (8天+1)*2
    第七天的桃子 等于(第八天的桃子+1)*2
     */
    public int peach(int day){
        if(day == 10){
            return 1;
        }else if(day >=1 && day <= 9){
            return (peach(day +1) +1)*2;
        }else{
            System.out.print("请输入天数1-10");
            return -1;
        }
    }
}

迷宫游戏

public class MeGong { 
    //编写一个main方法
    public static void main(String[] args) {
        int[][] map = new int[8][7];
        for(int i = 0; i < 7; i++){
            map[0][i] = 1;
            map[7][i] = 1;
        }
        for(int i = 0 ; i < 8 ; i++){
            map[i][0] = 1;
            map[i][6] = 1;
        }
        map[3][1] = 1;
        map[3][2] = 1;
        System.out.println("--------地图当前状态---------");
        for(int i = 0; i < map.length;i++){
            for(int j = 0; j < map[i].length; j++){
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
        T t1 = new T();
        t1.findway(map,1,1);
        System.out.println("--------找路后的状态---------");
        for(int i = 0; i < map.length;i++){
            for(int j = 0; j < map[i].length; j++){
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
    }
}
class T {
    //1. findWay 方法就是专门来找出迷宫的路径
    //2. 如果找到， 就返回 true ,否则返回 false
    //3. map 就是二维数组， 即表示迷宫
    //4. i,j 就是老鼠的位置， 初始化的位置为(1,1)
    //5. 因为我们是递归的找路， 所以我先规定 map 数组的各个值的含义
    // 0 表示可以走 1 表示障碍物 2 表示可以走 3 表示走过， 但是走不通是死路
    //6. 当 map[6][5] =2 就说明找到通路,就可以结束， 否则就继续找.
    //7. 先确定老鼠找路策略 下->右->上->左
    public boolean findway(int[][] map ,int i,int j){
        if(map[6][5] == 2){
            return true;
        }else{
            if(map[i][j] == 0){//0表示原始期盼中可以走的部分  
            //我们假定可以走通的
                map[i][j] = 2; //可以走通的情况下 判断怎么走
                if (findway(map,i+1,j)){ //向下
                    return true;
                }else if (findway(map,i,j+1)){//向右
                    return true;
                }else if(findway(map,i-1,j)){//向上
                    return true;
                }else if(findway(map,i,j-1)){
                    return true;
                }else{
                    map[i][j] = 3;
                    return false;
                }
            }else{//map[i][j]= 1 2 3
                return false;
            }
        }
    }
}