关于进制十六进制二进制十进制BCD码netty - 《Java 专栏》

转：https://zhuanlan.zhihu.com/p/38945098
https://www.cnblogs.com/summerdata/p/10722144.html

记牢下面对应
记牢下面对应
记牢下面对应
记牢下面对应

1 1 1 1 1 1 1 1
128 64 32 16 8 4 2 1
2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0

十六进制十进制二进制
FF 256 11111111
80 128 10000000
7F 127 01111111

一个数据(字节) = 01010101 （8个状态）用8个二进制数来表示

byte 8位二进制数
8位二进制数，太长了，每3位用1个数字表示，用3个8进制数就能表示，每4位用一个数字表示，用2个16进制数就可以表示

有符号byte 范围 (-128 ~ 127)
有符号byte 范围 (-128 ~ 127)

十六进制 （每4位二进制一分隔）每4位二进制表示1个十六进制数 2^4 = 16，十六进制0 ~ F 的这几个数字，一定能用 8,4,2,1这几个数字组合相加
八进制 每3位二进制表示1个八进制数 2^3 = 8

十六进制转二进制,用上边的记牢,但只用了其中 8421 法则,用到了 8 4 2 1 的哪一个相加之和等于该数，该位置就取1，否则取0
如:F:1111 F对应15=8+4+2+1 ，B对应11=8+2+1，4没有用对应的位置为0， 1011
FB 结果 11111011，组合即可
二进制转化为十六进制: 每4位使用 8421法则相加，得到10进制数，最大为15，再表示为十六进制即可
00101101
0010 = 2；
1101 = 8+4+1 = D；所以二进制 0b00101101 = 十六进制0x2D。

二进制转化为十进制
如 0b11111111，把对应的数加起来就可以了。
0b11111111 = 128+64+32+16+8+4+2+1 = 255 看到 255 有没有一种熟悉的感觉？
所以这时候再给你出道题，把 0b010110 转化成十进制你应该会了吧？
0b010110 = 16 + 4 + 2 = 22
这也就是把二进制数按权展开、相加即得十进制数,同样适用于八进制和十六进制转十进制
12^7 + 12^6 + 12^5 + 02^6 …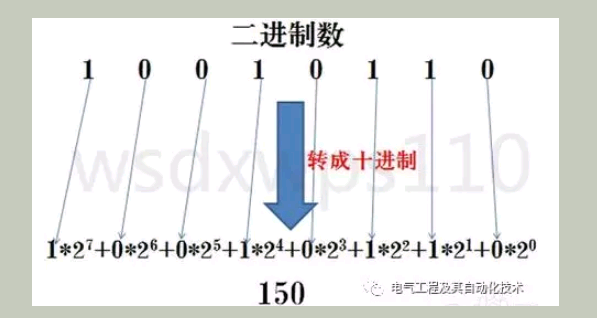

十进制转化为二进制
我们要把十进制如22，转为二进制就是：
22之内16有没有？那么在16对应的地方就有1。
22-16=6，那么8对应的就不存在了。
6之内有4对吧，那么4对应的就有1，6-4=2，那么2也有，2-2=0，所以1就没了。
所以最后的答案就是 22 = 0b10110。
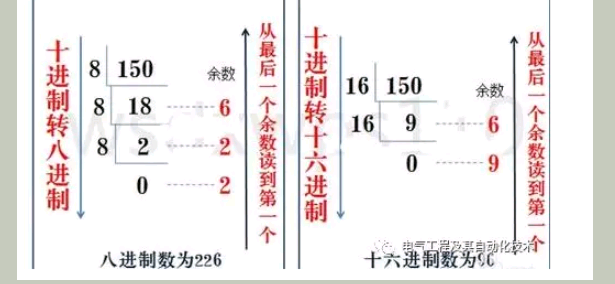
还有一种方法，就是十进制数除2取余法，即十进制数除2，余数为权位上的数，得到的商值继续除2，依此步骤继续向下运算直到商为0为止。同样适用于十进制转八进制和十六进制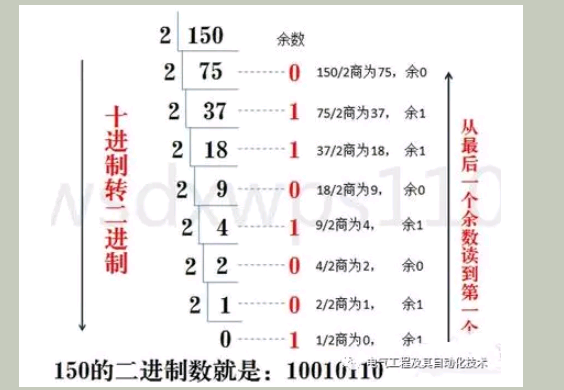

—————————————————————————
关于Byte 有意思的，上述8421法则
两位二进制数最大为 11 表示的整数 3 = 2 + 1 = 2^2 - 1
三位二进制数最大为111 表示的整数 7 = 4 +2 +1 = 2^3 - 1
四位二进制数最大为1111 表示的整数 15 = 8 + 4 +2 +1 = 2^4 - 1
以此类推
七位二进制数最大为1111111 表示的整数 127 = 64 + 32 + 16 + 8 + 4 +2 +1 = 2^7 - 1
八位二进制数最大为11111111 表示的整数 255 = 128 + 64 + 32 + 16 + 8 + 4 +2 +1 = 2^8 - 1

1个字节是8位二进制数，本应表示最大值为 255 ，但 java byte 类型是有符号整型，最高位是符号位 0为正 1为负，剩余7位为数据，则java byte正数最大表示为127 ，负数为 -128
——————————————————————————————————-
关于Java Byte 的取值范围大家都知道（-128 ~ 127），那么-128 和 127 这两个数是怎么计算的呢？
概念：负数的补码是该数绝对值的原码按位取反 ,然后对整个数加 1
在计算机内，定点数有3种表示法：原码、反码和补码
[原码]就是前面所介绍的二进制定点表示法，即最高位为符号位，“0”表示正，“1”表示负，其余位表示数值的大小。
[反码]表示法规定：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。
[补码]表示法规定：正数的补码与其原码相同；负数的补码是在其反码的末位加1。
Java使用补码来表示二进制数 ,在补码表示中 ,最高位为符号位 ,正数的符号位为 0,负数为 1。
现在进行java Byte 取值范围分析：
1、确定byte是1个字节，也就是8位
2、对于计算机来说，二进制最大的正数是01111111 转换成十进制为：127
3、最小的负数： 10000000，即-128
二进制负数的值：取反加一，所以 10000000 的值为：
1. 取反 -> 01111111 127
2. 加一 -> 128
3. 加上符号： -128
负数的二进制 = 正数(该数的绝对值)的二进制反码 + 1

例如：-5
第一步取绝对值：-5 的绝对值：5
第二步转二进制：5的二进制：0000 0101
第三步取反码： 0000 0101 的反码 1111 1010
第四步加一： 1111 1010 加一 1111 1011————————————————

Java 用Byte存储 255 https://blog.csdn.net/qq_37855749/article/details/115736609
-128 ~ 127
0 ~ 255

-1 -2 … -126 -127 -128
255 254 … 130 129 128

byte a= (byte) 255;
System.out.println(Byte.toUnsignedInt(a));
或者
byte a = (_byte) _0xff; //(byte) 255
System.out.println(a & 0xff);
结果都是255
整型0-225 转十六进制字符串
Integer.toHexString(buf[i] & 0xFF)
String.format(“%02X”, b);

关于BCD码
采用BCD码,1位十进制数要用4位二进制数表示, 一个字节其有8个二进位位，所以能存放2个BCD码，恰好一个字节可以由2个十六进制数表示，
如：字符串 12
二进制 0001 0010
十六进制 0x12 （每4位二进制一分隔）
https://blog.csdn.net/qq_33750826/article/details/53004685
Java的String数字和BCD码相互转换
https://blog.csdn.net/o0daxu0o/article/details/120924462
累加和校验实现方式16进制
每个字节累加得出整数计算出和，用上面除16取余法，2次，即得到从低到高最后2位十六进制，或者用和对256求余再转为16进制，即可

关于Netty buffer

java 通过移位的方法做int字节转换
/
@author: qzf
@date: 2022/5/18 14:31
@describe: byte转无符号整型long(低位在后，高位在前)
@param:
@return:
/
public static long bytesToLongAhead(byte[] bs) throws Exception {
int bytes = bs.length;
if(bytes == 0){
return 0;
}
if(bytes > 1) {
if((bytes % 2) != 0 || bytes > 8) {
throw new Exception(“not support”);
}}
switch(bytes) {
case 0:
return 0;
case 1:
return (long)((bs[0] & 0xff));
case 2:
return (long)((bs[0] & 0xff) <<8 | (bs[1] & 0xff));
case 4:
return (long)((bs[0] & 0xffL) <<24 | (bs[1] & 0xffL) << 16 | (bs[2] & 0xffL) <<8 | (bs[3] & 0xffL));
case 8:
return (long)((bs[0] & 0xffL) <<56 | (bs[1] & 0xffL) << 48 | (bs[2] & 0xffL) <<40 | (bs[3] & 0xffL)<<32 |
(bs[4] & 0xffL) <<24 | (bs[5] & 0xffL) << 16 | (bs[6] & 0xffL) <<8 | (bs[7] & 0xffL));
default:
throw new Exception(“not support”);
}
//return 0;
}
/
@author: qzf
@date: 2022/5/18 14:31
@describe: long无符号整型转byte(低位在后，高位在前)
@param:
@return:
/
public static byte[] longToBytesAhead(long value,int length) {
byte[] src = new byte[length];
if(value == 0){
return src;
}
if(length % 2 != 0){
return src;
}
switch (length){
case 1:
src[0] = (byte) (value & 0xFF);
break;
case 2:
src[0] = (byte) ((value >> 8) & 0xFF);
src[1] = (byte) (value & 0xFF);
break;
case 4:
src[0] = (byte) ((value >> 24) & 0xFF);
src[1] = (byte) ((value >> 16) & 0xFF);
src[2] = (byte) ((value >> 8) & 0xFF);
src[3] = (byte) (value & 0xFF);
break;
case 8:
src[0] = (byte) ((value >> 56) & 0xFF);
src[1] = (byte) ((value >> 48) & 0xFF);
src[2] = (byte) ((value >> 40) & 0xFF);
src[3] = (byte) ((value >> 36) & 0xFF);
src[4] = (byte) ((value >> 24) & 0xFF);
src[5] = (byte) ((value >> 16) & 0xFF);
src[6] = (byte) ((value >> 8) & 0xFF);
src[7] = (byte) (value & 0xFF);
break;
}

    return src;<br />    }