贪心算法

贪心算法（greedy algorithm），又称贪婪算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择，不能回退。动态规划则会保存以前的运算结果，并根据以前的结果对当前进行选择，有回退功能。

具体例子

1. 模拟行走机器人(LeetCode-874)

image.png
解法：

  1. /**
  2.  * @param {number[]} commands
  3.  * @param {number[][]} obstacles
  4.  * @return {number}
  5.  */
  6. var robotSim = function(commands, obstacles) {
  7.   const len = commands.length
  8.   // 利用对象存储障碍点
  9.   const map = {}
  10.   obstacles.forEach(item => {
  11.     map[`${item[0]},${item[1]}`] = true
  12.   })
  13.   // 定义移动的方向
  14.   let direction = 0
  15.   const directionX = [0, 1, 0, -1]
  16.   const directionY = [1, 0, -1, 0]
  17.   // 初始化机器人的坐标
  18.   let x = y = ans =  0
  20.   for (let i = 0; i < len; i++) {
  21.     // 当命令为-1、-2的时候改变方向
  22.     if (commands[i] === -2) {
  23.       direction = (direction + 3) % 4;
  24.     } else if (commands[i] === -1) {
  25.       direction = (direction + 1) % 4;
  26.     } else if (commands[i] >= 1 && commands[i] <= 9) {
  27.       // 对移动节点的不常的进行便利，每次移动异步，每次判断下一个节点是不是障碍点
  28.       // 把问题分化
  29.       for (let j = 0; j < commands[i]; j++) {
  30.         let X = x + directionX[direction]
  31.         let Y = y + directionY[direction]
  32.         if (!map[`${X},${Y}`]) {
  33.           x = X
  34.           y = Y
  35.         }
  36.       }
  37.       ans = Math.max(ans, Math.pow(x, 2) + Math.pow(y, 2))
  38.     }
  39.   }
  40.   return ans
  41. };

2. 分饼干(LeetCode-455)

image.png
解法：

/**
 * @param {number[]} g
 * @param {number[]} s
 * @return {number}
 */
var findContentChildren = function(g, s) {
  s = s.sort((a, b) => a- b)
  g = g.sort((a, b) => a- b)
  const len = g.length
  const endLen = s.length
  // s便利的位置
  let index = 0
  // g便利的位置同时也是结果
  let res = 0
  // 当有一个便利结束时，结束查找
  while (res < len && index < endLen) {
    if (s[index] >= g[res]) {
      res++
    }
    index++
  }
  return res
};

3. 换酒问题(LeetCode-1518)

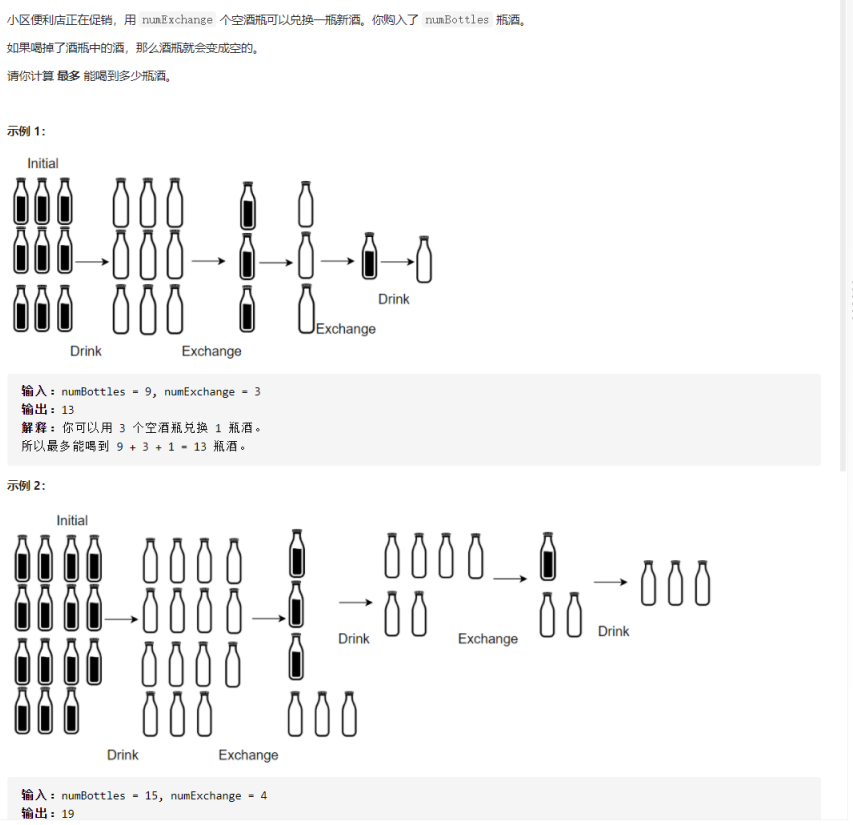
image.png
解法：

/**
 * @param {number} numBottles
 * @param {number} numExchange
 * @return {number}
 */
var numWaterBottles = function(numBottles, numExchange) {
  // 空瓶数量
  let nullBottles = numBottles
  // 每次用空瓶兑换完啤酒后空瓶剩余的数量
  let remainder = 0
  let count = numBottles
  while (nullBottles >= numExchange) {
    nullBottles -= numExchange
    count++
    nullBottles++
  }
  return count
};

4. 最后一块石头的重量(LeetCode-1046)

image.png
解法：

/**
 * @param {number[]} stones
 * @return {number}
 */
var lastStoneWeight = function(stones) {
    stones = stones.sort((a, b) => b - a)
    while (stones.length >= 2) {
      const [pre1, pre2] = stones.splice(0, 2)
      if (pre1 !== pre2) {
        // 最好使用二分法插入
        stones.push(Math.abs(pre1 - pre2))
        stones.sort((a, b) => b - a)
      }
    }
    return stones[0] || 0
};