广度优先搜索

广度优先搜索算法（英语：Breadth-First Search，缩写为BFS），是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。 ——维基百科。

实际应用

BFS在求解最短路径或者最短步数上有很多的应用。

对比

深度优先搜索

深度优先搜索用栈（stack）来实现，整个过程可以想象成一个倒立的树形：
1、把根节点压入栈中。
2、每次从栈中弹出一个元素，搜索所有在它下一级的元素，把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
3、找到所要找的元素时结束程序。
4、如果遍历整个树还没有找到，结束程序。

广度优先搜索

广度优先搜索使用队列（queue）来实现，整个过程也可以看做一个倒立的树形：
1、把根节点放到队列的末尾。
2、每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
3、找到所要找的元素时结束程序。
4、如果遍历整个树还没有找到，结束程序。

具体例子

1. 二叉树最小深度（LeetCode-111）

解法：

var minDepth = function(root) {
  if (!root) return 0
  const stack = []
  // 把root节点压入stack中
  stack.push([root, 1])
  let depth = 0
  while (stack.length) {
    // 取出首位
    const current = stack.shift()
    const currentRoot = current[0]
    depth = current[1]
    // 如果当前节点没有下一级了，则为最短路径
    if (!currentRoot.left && !currentRoot.right) break
    if (currentRoot.left) stack.push([currentRoot.left, depth + 1])
    if (currentRoot.right) stack.push([currentRoot.right, depth + 1])
  }
  return depth
};

2. 二叉树的层次遍历2（LeetCode-107）

解法：

var levelOrderBottom = function(root) {
  if(!root) return []
  const stack = []
  // 结果数组
  const ans = []
  // 当前深度
  let depth = 0
  stack.push([root, 1])
  while (stack.length) {
    const current = stack.shift()
    const currentRoot = current[0]
    // 如果迭代深度比当前深度大则新增一个数组
    if (current[1] > depth) {
      ans.unshift([currentRoot.val])
      depth = current[1]
    } else {
      ans[0].push(currentRoot.val)
    }
    if (currentRoot.left) stack.push([currentRoot.left, depth + 1])
    if (currentRoot.right) stack.push([currentRoot.right, depth + 1])
  }
  return ans
};

3. 二叉树的堂兄弟(LeetCode-993)

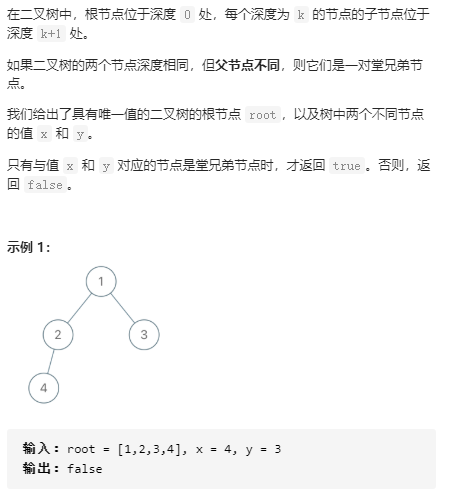
解法：

var isCousins = function(root, x, y) {
  if (!root) return true
  const stack = []
  let activeTree = null, activeDep = 0, ans = true
  stack.push([root, 1, null])
  while (stack.length) {
    const current = stack.shift()
    const currentRoot = current[0]
    // 如果不在同一层次 直接返回false
    if (activeDep && current[1] > activeDep) {
      ans = false
      break
    }
    // 匹配节点时
    if (currentRoot.val === x || currentRoot.val === y) {
      // 第一次匹配进行赋值保存
      if (!activeDep) {
        activeDep = current[1]
        activeTree = current[2]
      } else {
        // 第二次匹配如果深度不同或者父节点相同 直接返回fals
        if (activeDep !== current[1] || activeTree === current[2] ) {
          ans = false
        }
        break
      }
    }
    if (currentRoot.left) stack.push([currentRoot.left, current[1] + 1 , currentRoot])
    if (currentRoot.right) stack.push([currentRoot.right, current[1] + 1 , currentRoot])
  }
  return ans
};