位掩码

计算机组成原理 位掩码

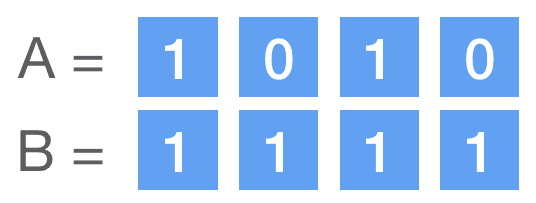
位运算符

在了解“位掩码”之前，首先要学会位运算符。
在计算机中数据其实都是以二进制的形式所储存的，而位运算符则可以对二进制数据进行操作。举个简单的例子，给定两个二进制数据（其中 0b 是二进制数据的前缀）：

const A = 0b1010
const B = 0b1111

1、按位非运算符 ~

对每一位执行非（NOT）操作，也可以理解为取反码。

2、按位与运算符 &

对每一位执行与（AND）操作，只要对应位置均为 1 时，结果才为 1，否则为 0。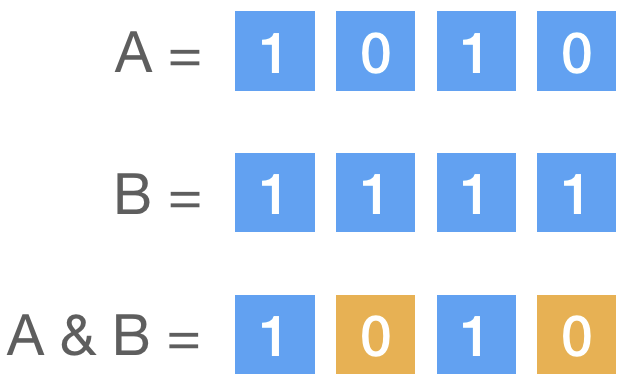

3、按位或运算符 |

对每一位执行或（OR）操作，只要对应位置有一个 1 时，结果就为 1。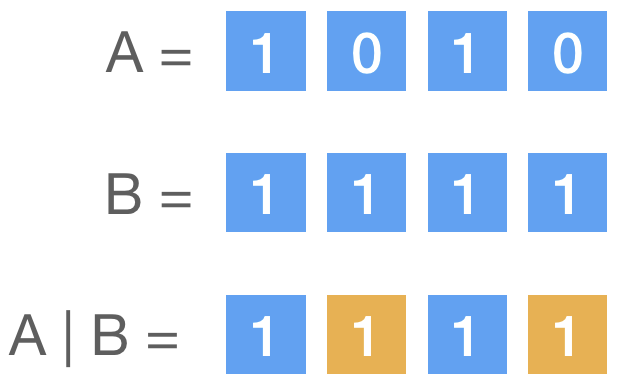

4、按位异或运算符 ^

对每一位执行异或（XOR）操作，当对应位置有且只有一个 1 时，结果就为 1，否则为 0。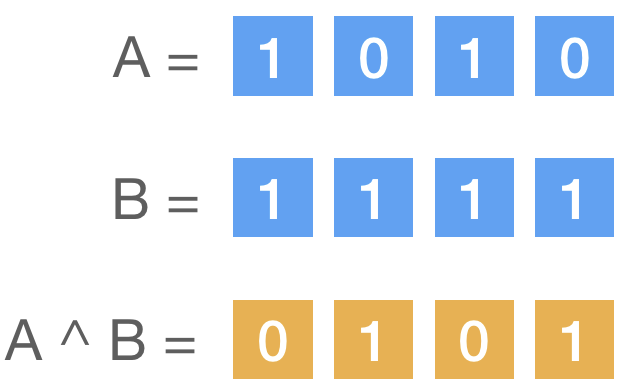

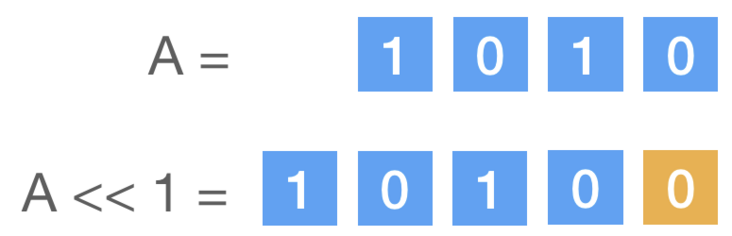
5、左移运算符 <<

将数据向左移动一定的位（<32），右边用 0 填充。

6、右移运算符 >>

将数据向右移动一定的位（<32），遗弃被丢出的位。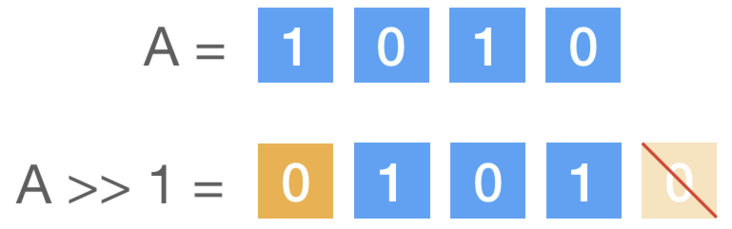

权限系统

假设有一个权限系统，它通过 JSON 的方式记录了某个用户的权限开通情况（姑且假设权限集是 CURD)：

const permission = {
  create: false,
  update: false,
  read: true,
  delete: false,
}

如果把 false 写成 0，true 写成 1，那么这个 permisson 对象可以简写为 0b0010。

const permission = {
  create: false,
  update: false,
  read: true,
  delete: false,
}
// 从左往右，依次为 create, update, read, delete 所对应的值
const permissionBinary = 0b0010

对于 JSON 对象的权限集，如果要查看或者修改该用户的某些权限，只需要通过形如 permission.craete 的普通对象操作即可。那么如果对于二进制形式的权限集，又应该如何进行查看或者修改的操作呢？接下来就开始使用奇怪的知识——位掩码来进行了。

位掩码

首先进行名词解释，什么是”位掩码“。
位掩码（BitMask），是”位（Bit）“和”掩码（Mask）“的组合词。”位“指代着二进制数据当中的二进制位，而”掩码“指的是一串用于与目标数据进行按位操作的二进制数字。组合起来，就是”用一串二进制数字（掩码）去操作另一串二进制数字“的意思。
明白了位掩码的作用以后，就可以通过它来对权限集二进制数进行操作了。

1、查询用户是否拥有某个权限

已知用户权限集二进制数为 permissionBinary = 0b0010。如果想知道该用户是否存在 update 这个权限，可以先给定一个位掩码 mask = 0b1。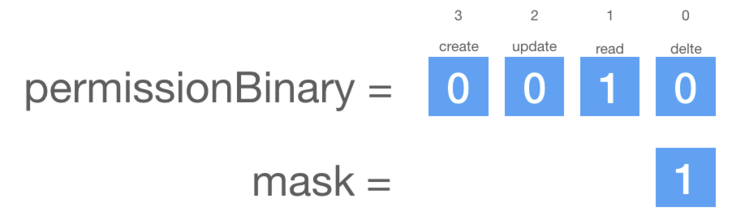

由于 update 位于右数第三项，所以只需要把位掩码向左移动两位，剩余位置补0。最后和权限集二进制数进行按位与运算即可得到结果。

最后算出来的 result 为 0b0000，使用 Boolean() 函数处理之即可得到 false 的结果，也就是说该用户的 update 权限为 false。

// 从左往右，依次为 create, update, read, delete 所对应的值
const permissionBinary = 0b0010
// 由于 update 位于右数第三位，因此只需要让掩码向左移动2位即可
const mask = 0b1 << 2
const result = permissionBinary & mask
Boolean(result) // false

2、修改用户的某个权限

明白了如何用位掩码来查询权限后，要修改对应的权限也就手到擒来了，无非就是换一种位运算。假设还是 update 权限，如果想把它修改成 true，可以这样做：

只需要把按位与改为按位异或即可，代码如下：

// 从左往右，依次为 create, update, read, delete 所对应的值
const permissionBinary = 0b0010
// 由于 update 位于右数第三位，因此只需要让掩码向左移动2位即可
const mask = 0b1 << 2
const result = permissionBinary ^ mask
parseInt(result).toString(2) // 0b0110

脏数据记录

前文例子中的权限系统仅有区区4个数据的处理，位掩码技术显得复杂又小题大做。那么有没有什么场景是真的适合使用位掩码的呢？脏数据记录就是其中一个。
假设存在着一份原始数据，其值如下：

let A = 'a'
let B = 'b'
let C = 'c'
let D = 'd'

给定一个二进制数，从左往右分别对应着 A/B/C/D 的状态：

let O = 0b0000 // 十进制 0

则数据一旦发生了修改，都可以用对应的比特位来表示

// 当且仅当 A 发生了修改
O = 0b1000 // 十进制 8
// 当且仅当 B 发生了修改
O = 0b0100 // 十进制 4
// 当且仅当 C 发生了修改
O = 0b0010 // 十进制 2
// 当且仅当 D 发生了修改
O = 0b0001 // 十进制 1

同理，当多个数据发生了修改时，则可以同时表示

// 当 A 和 B 发生了修改
O = 0b1100 // 十进制 12
// 当 A/B/C 都发生了修改
O = 0b1110 // 十进制 14

通过这个思路，应用排列组合的思想，可以很快知道只需要仅仅 4 个比特位，就可以表达 16 种数据变化的情况。由于二进制和十进制可以相互转化，因此只需要区区 16 个十进制数，就可以完整地表达 A/B/C/D 这四个数据的变化情况，也就是脏数据追踪。举个例子，给定一个脏数据记录 14，二进制转换为 0b1110，因此表示 A/B/C 的数据被修改了。
Svelte 这个框架，就是通过这个思路来实现响应式的：

if ( A 数据变了 ) {
  更新A对应的DOM节点
}
if ( B 数据变了 ) {
  更新B对应的DOM节点
}
/** 转化成伪代码 **/
if ( dirty & 8 ) { // 8 === 0b1000
  更新A对应的DOM节点
}
if ( dirty & 4 ) { // 4 === 0b0100
  更新B对应的DOM节点
}

更多具体的介绍可以查看《新兴前端框架 Svelte 从入门到原理》。

老鼠喝毒药

除了用来做脏数据记录以外，位掩码也能够用来处理经典的”老鼠喝毒药“的问题。

有 1000 瓶水，其中有一瓶有毒，小白鼠只要尝一点带毒的水24小时后就会死亡，问至少要多少只小白鼠才能在24小时内鉴别出哪瓶水有毒？

简化一下问题，假设只有 8 瓶水，其编号用二进制表示：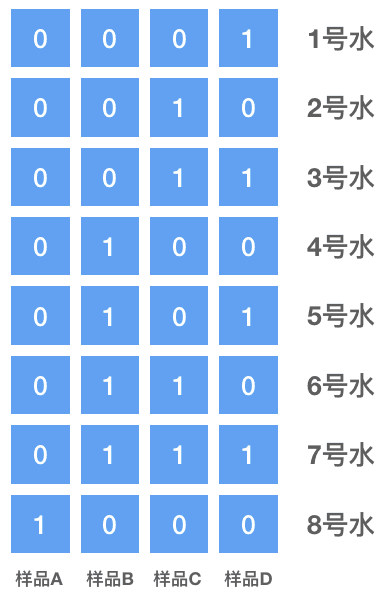

接着按照图示的方式对水瓶的水进行混合，得到样品 A/B/C/D，取4只老鼠编号为 a/b/c/d 分别喝下对应的水，得到如下的表格：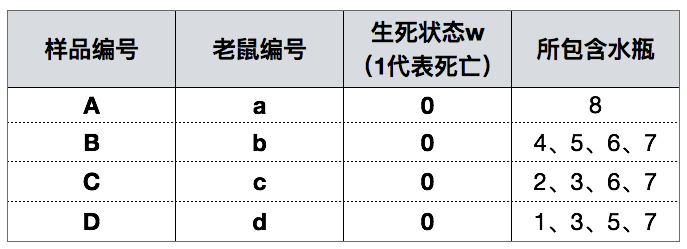

在 24 小时候，统计老鼠的死亡情况，汇总后可以得到表格和结果：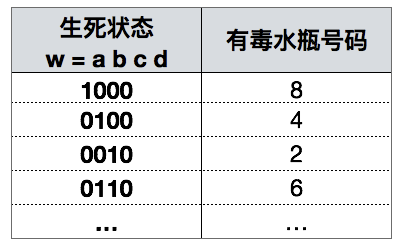

答案呼之欲出，由于 8 瓶水可以兑出 4 份样品，因此只需要 4 只老鼠即可在 24 小时后确定到底哪一瓶水是有毒的。回到题目，如果是 1000 瓶水，只需要知道第 1000 号的二进制数 0b1111101000即可。该二进制数一共有 10 个比特位，意味着 1000 瓶水可以兑出 10 份样品，也就是说只需要 10 只老鼠，就可以完成测试任务。