引入

斐波拉契数列

暴力搜索

  1.     static int fib(int n) {
  2.         if (n == 1 || n == 2) return 1;
  3.         return fib(n - 1) + fib(n - 2);
  4.     }

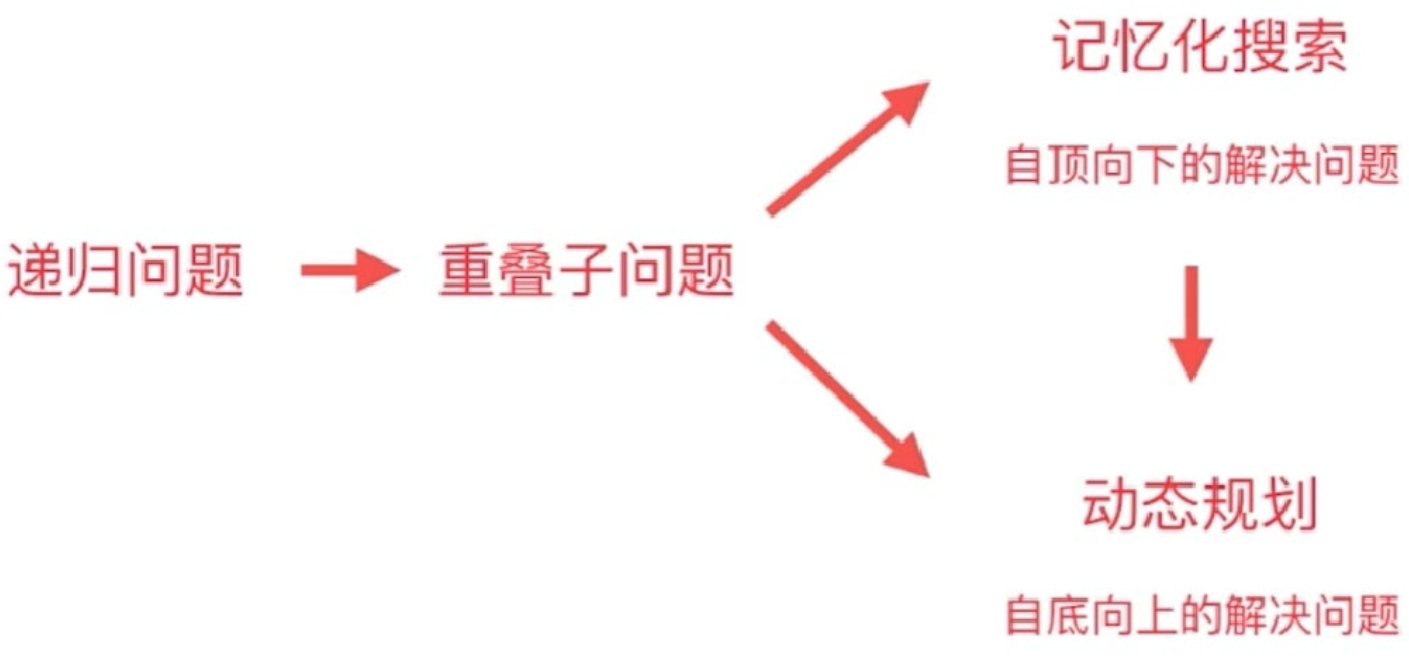
记忆化搜索（备忘录）

自上而下的解决问题

  1. static int[] memo = new int[100];
  2. static int fib2(int n) {
  3.     if (n == 1 || n == 2) return 1;
  4.     if (memo[n] == 0)
  5.         memo[n] = fib2(n - 1) + fib2(n - 2);
  6.     return memo[n];
  7. }

动态规划

自下而上的解决问题

  1.     static int fib3(int n) {
  2.         int[] memo = new int[100];
  3.         memo[0] = 0;
  4.         memo[1] = 1;
  5.         for (int i = 2; i <= n; i++)
  6.             memo[i] = memo[i - 1] + memo[i - 2];
  7.         return memo[n];
  8.     }

image.png
习题
leetcode120
image.png
基本思路

  1. class Solution {
  2.     public int minimumTotal(List<List<Integer>> triangle) {
  3.         int n = triangle.size();
  4.         int[][] dp = new int[n][n];
  5.         for (int i = n - 1; i >= 0; i--) {
  6.             for (int j = 0; j < triangle.get(i).size(); j++) {
  7.                 if (i == n - 1) {
  8.                     dp[i][j] = triangle.get(i).get(j);
  9.                 }
  10.                 else
  11.                     dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);
  12.             }
  13.         }
  14.         return dp[0][0];
  15.     }
  16. }

优化，增加一行数组避免判断，由于每一层状态只与下一层有关，优化一维空间。

  1. class Solution {
  2.     public int minimumTotal(List<List<Integer>> triangle) {
  3.         int n = triangle.size();
  4.         int[] dp = new int[n + 1];
  5.         for (int i = n - 1; i >= 0; i--) {
  6.             for (int j = 0; j < triangle.get(i).size(); j++) {
  7.                 dp[j] = Math.min(dp[j], dp[j + 1]) + triangle.get(i).get(j);
  8.             }
  9.         }
  10.         return dp[0];
  11.     }
  12. }

leetcode64
image.png

递归1

  1. class Solution {
  2.     int res = Integer.MAX_VALUE;
  3.     public int minPathSum(int[][] grid) {
  4.         dfs(grid, 0, 0, grid[0][0]);
  5.         return res;
  6.     }
  8.     void dfs(int[][] g, int x, int y, int cur) {
  9.         if (x == g.length - 1 && y == g[0].length - 1) {
  10.             res = Math.min(res, cur);
  11.             return;
  12.         }
  13.         if (y + 1 < g[0].length)
  14.             dfs(g, x, y + 1, cur + g[x][y + 1]);
  15.         if (x + 1 < g.length)
  16.             dfs(g, x + 1, y, cur + g[x + 1][y]);
  18.     }
  19. }

递归2+备忘录

  1. class Solution {
  2.     int[][] memo = new int[210][210];
  3.     public int minPathSum(int[][] grid) {
  4.         for (int i = 0; i < memo.length; i++)
  5.             Arrays.fill(memo[i], -1);
  7.         return dfs(grid, 0, 0);
  8.     }
  9.     // 从x y位置到终点的最小总和 cur为已消耗
  10.     int dfs(int[][] g, int x, int y) {
  11.         if (x == g.length || y == g[0].length) return Integer.MAX_VALUE;
  12.         if (x == g.length - 1 && y == g[0].length - 1) {
  13.             return g[x][y];
  14.         }
  15.         if (memo[x][y] != -1)
  16.             return memo[x][y];
  17.         memo[x][y] = Math.min(dfs(g, x + 1, y), dfs(g, x, y + 1)) + g[x][y];
  18.         return memo[x][y];
  19.     }
  20. }

动态规划

class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length;
        if (n == 0) return 0;
        int m = grid[0].length;
        int[][] dp = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (i == 0 && j == 0)
                    dp[i][j] = grid[i][j];
                else if (i == 0)
                    dp[i][j] = grid[i][j] + dp[i][j - 1];
                else if (j == 0)
                    dp[i][j] = grid[i][j] + dp[i - 1][j];
                else 
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[n - 1][m - 1];
    }
}