背包问题类似问题

416

核心思想：0-1背包问题 能否用nums的某些数，填充sum / 2的空间
dp[n][C] = dp[n - 1][C] || dp[n - 1][C - nums[n]] (使用第n个物品填充 或 不使用)

class Solution {
    // 背包问题（能否用nums的某些数，填充sum / 2的空间）
    // dp[n][C] = dp[n - 1][C] || dp[n - 1][C - nums[n]] (使用第n个物品填充 或 不使用)
    public boolean canPartition(int[] nums) {
        if (nums.length == 0) return false;
        int sum = Arrays.stream(nums).sum();
        int n = nums.length;
        if (sum % 2 != 0) return false;
        int C = sum / 2;
        boolean[][] dp = new boolean[n][C + 1];
        for (int i = 0; i <= C; i++)
            dp[0][i] = (nums[0] == i);
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= C; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= nums[i])
                    dp[i][j] |= dp[i - 1][j - nums[i]];
            }
        }
        return dp[n - 1][C];
    }
}

空间优化

class Solution {
    // 背包问题（能否用nums的某些数，填充sum / 2的空间）
    // dp[n][C] = dp[n - 1][C] || dp[n - 1][C - nums[n]] (使用第n个物品填充 或 不使用)
    public boolean canPartition(int[] nums) {
        if (nums.length == 0) return false;
        int sum = Arrays.stream(nums).sum();
        int n = nums.length;
        if (sum % 2 != 0) return false;
        int C = sum / 2;
        boolean[] dp = new boolean[C + 1];
        for (int i = 0; i <= C; i++)
            dp[i] = (nums[0] == i);
        for (int i = 1; i < n; i++) {
            for (int j = C; j >= 0; j--) {
                if (j >= nums[i])
                    dp[j] |= dp[j - nums[i]];
            }
        }
        return dp[C];
    }
}

322

递归+备忘录

class Solution {
    int[] memo;
    public int coinChange(int[] coins, int amount) {
        memo = new int[amount+1];
        Arrays.fill(memo, -1);
        int res = dfs(coins, amount);
        return res > 0x3f3f3f3f / 2 ? -1 : res;
    }
    int dfs(int[] coins, int amount) {
        if (amount == 0)
            return 0;
        if (amount < 0) return 0x3f3f3f3f;
        if (memo[amount] != -1) return memo[amount];
        int res = 0x3f3f3f3f;
        for (int i = 0; i < coins.length; i++)
            res = Math.min(res, dfs(coins, amount - coins[i]) + 1);
        memo[amount] = res;
        return res;
    }
}

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int coin : coins)
                if (i >= coin)
                    dp[i] = Math.min(dp[i], dp[i - coin] + 1);
        }
        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }
}

377

474

class Solution {
    // 没有使用备忘录
    // 两个条件的背包问题， 0  1 个数分别不能超过m n，能偷走的最多东西
    public int findMaxForm(String[] strs, int m, int n) {   
        return dfs(strs, m, n, 0);
    }

    int dfs(String[] strs, int m, int n, int start) {
        // 这里注意是<0而不是<=0,一个等于0另一个不等于0也可能是正常情况
        if (m < 0 || n < 0 || strs.length == start) return 0;
        int res = dfs(strs, m, n, start + 1);
        int ms = getZero(strs[start]), ns = strs[start].length() - ms;
        if (m >= ms && n >= ns)
            res = Math.max(res, dfs(strs, m - ms, n - ns, start + 1) + 1);
        return res;
    }

    int getZero(String s) {
        int res = 0;
        for (char ch : s.toCharArray())
            if (ch == '0')
                res++;
        return res;
    }
}

动态规划 模拟背包问题
初始化 边界条件。
三个维度

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][][] dp = new int[strs.length][m + 1][n + 1];

        int oneNum = 0, zeroNum = 0;
        char[] charArray = strs[0].toCharArray();
        for (char c : charArray) {
            if (c == '0') zeroNum++;
            else oneNum++;
        }

        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                if (i >= zeroNum && j >= oneNum)
                    dp[0][i][j] = 1;
            }
        }

        for (int i = 1; i < strs.length; i++) {
            oneNum = 0; zeroNum = 0;
            charArray = strs[i].toCharArray();
            for (char c : charArray) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k <= n; k++) {
                    dp[i][j][k] = dp[i - 1][j][k];
                    if (j >= zeroNum && k >= oneNum)
                        dp[i][j][k] = Math.max(dp[i - 1][j - zeroNum][k - oneNum] + 1, dp[i][j][k]);
                }       
            }
        } 
        return dp[strs.length  - 1][m][n];
    }
}

缩小到2维

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][]dp = new int[m+1][n+1];
        for (String str : strs) { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            char[] charArray = str.toCharArray();
            for (char c : charArray) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
}

139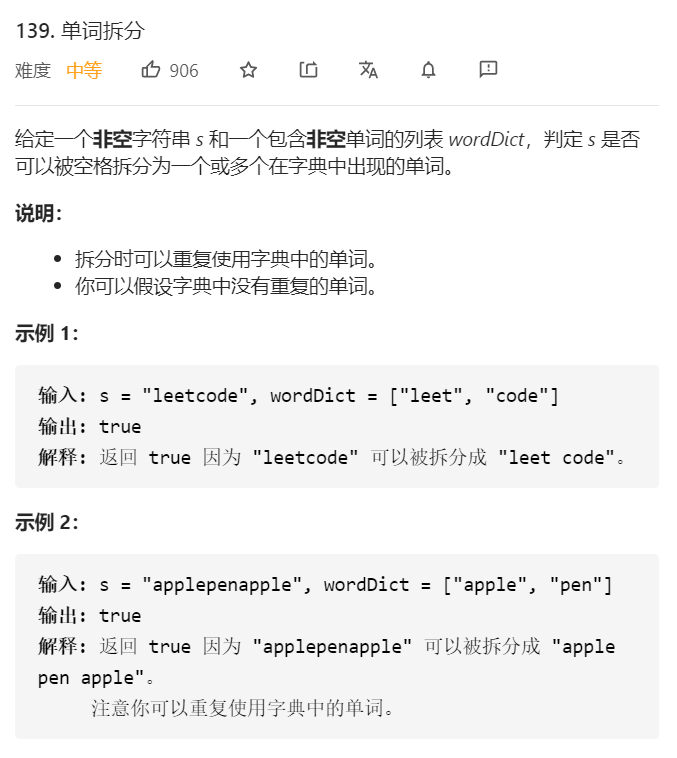

递归

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        return dfs(s, wordDict);
    }

    boolean dfs(String s, List<String> wordDict) {
        if (s.length() == 0) return true;
        boolean res = false;

        for (int i = 0; i < wordDict.size(); i++) {
            String cur = wordDict.get(i);
            if (s.indexOf(cur) == 0)
                res |= dfs(s.substring(cur.length()), wordDict);
        }
        return res;
    }
}

递归+备忘录

class Solution {

    int[] memo;

    public boolean wordBreak(String s, List<String> wordDict) {
        memo = new int[s.length()];
        Arrays.fill(memo, -1);
        return dfs(s, wordDict, 0);
    }

    boolean dfs(String s, List<String> wordDict, int start) {
        if (start == s.length()) return true;
        boolean res = false;
        if (memo[start] != -1) return memo[start] == 1;
        for (int i = 0; i < wordDict.size(); i++) {
            String cur = wordDict.get(i);
            if (s.indexOf(cur, start) == start)
                res |= dfs(s, wordDict, start + cur.length());
        }
        memo[start] = res ? 1 : 0;
        return res;
    }
}

动态规划（TO DO）
494

递归+备忘录

class Solution {
    int[][] memo = new int[3000][30];
    public int findTargetSumWays(int[] nums, int s) {
        if (Arrays.stream(nums).sum() < s) return 0;
        return dfs(nums, s, 0);
    }

    int dfs(int[] nums, int s, int start) {
        if (start == nums.length && s == 0)
            return 1;
        if (start == nums.length) 
            return 0;
        if (memo[s + 1000][start] != 0) return memo[s + 1000][start];
        int minus = dfs(nums, s + nums[start], start + 1);
        int add = dfs(nums, s - nums[start], start + 1);
        memo[s + 1000][start] = minus + add;
        return minus + add;
    }
}

动态规划

class Solution {
    public int findTargetSumWays(int[] nums, int s) {
        int sum = Arrays.stream(nums).sum();
        if (sum < s) return 0;
        // 向右平移了sum个单位，能得到的负最大值移动到0.
        int[][] dp = new int[nums.length][2 * sum + 1];
        if (nums[0] == 0) {
            // 第一个数等于0 ，得到0（sum - sum）的方法数是2（+ 或者 -）
            dp[0][sum] = 2;
        } else {
            // 否则 +第一个数和 - 第一个数的位置的方法数为1
            dp[0][sum + nums[0]] = 1;
            dp[0][sum - nums[0]] = 1;
        }
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
                int l = j - nums[i] < 0 ? 0 : j - nums[i];
                int r = j + nums[i] > 2 * sum ? 0 : j + nums[i];
                dp[i][j] = dp[i - 1][l] + dp[i - 1][r];
            }
        }

    }
}

1049. 最后一块石头的重量 II

开始的思路是贪心：每次取出最大的和次大的粉碎然后放回，不满足这个性质。

转换成01背包问题，求两堆石头的最小差值。由于石头总和为sum.则问题转换成了
背包最多装sum / 2的石头,stones数组里有一大堆石头。求如何装能装下最多重量石头。

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = Arrays.stream(stones).sum();
        int[][] dp = new int[stones.length][sum / 2 + 1];
        for (int i = 0; i < sum / 2 + 1; i++)
            if (i >= stones[0])
                dp[0][i] = stones[0];
        for (int i = 1; i < stones.length; i++) {
            for (int j = 0; j < sum / 2 + 1; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j >= stones[i]) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - stones[i]] + stones[i]);
                }
            }
        }
        int val = dp[stones.length - 1][sum / 2];
        System.out.println(val);
        return Math.abs(sum - 2 * val);
    }
}