188. 买卖股票的最佳时机 IV

什么叫手撕代码？就是做不出来很烦躁🤬就想把这题给撕了炖了🍲 炖了炖了🍲🍲🍲🍲🍲🍲🍲

分享一下解法，有用三维数组的，也有用二维数组的，还有用一维数组的

emmm，先抛出一个问题，不知道你们有没有理解题目到底怎么定义的交易？
若：
买+卖 = 一次交易
那么：
一次买 = 几次交易？🌝0.5？
一次卖 = 几次交易？🌝0.5？

若：
一次买 = 一次交易
一次卖 = 一次交易
那么：
买 + 卖 = 几次交易？🌝

先啃个水果压压惊🥑🥑🥑，哼，这个地方就是个坑，我在这个坑里面蹲了好久才爬出来
这里是需要我们自己去完善这个定义从而建立我们的dp数组的

三维数组的解法：
如果我们把买+卖算一次交易
那么这道题的限制是交易数，天数，手上有没有股票(有股票就不能买，没有股票就不能卖)
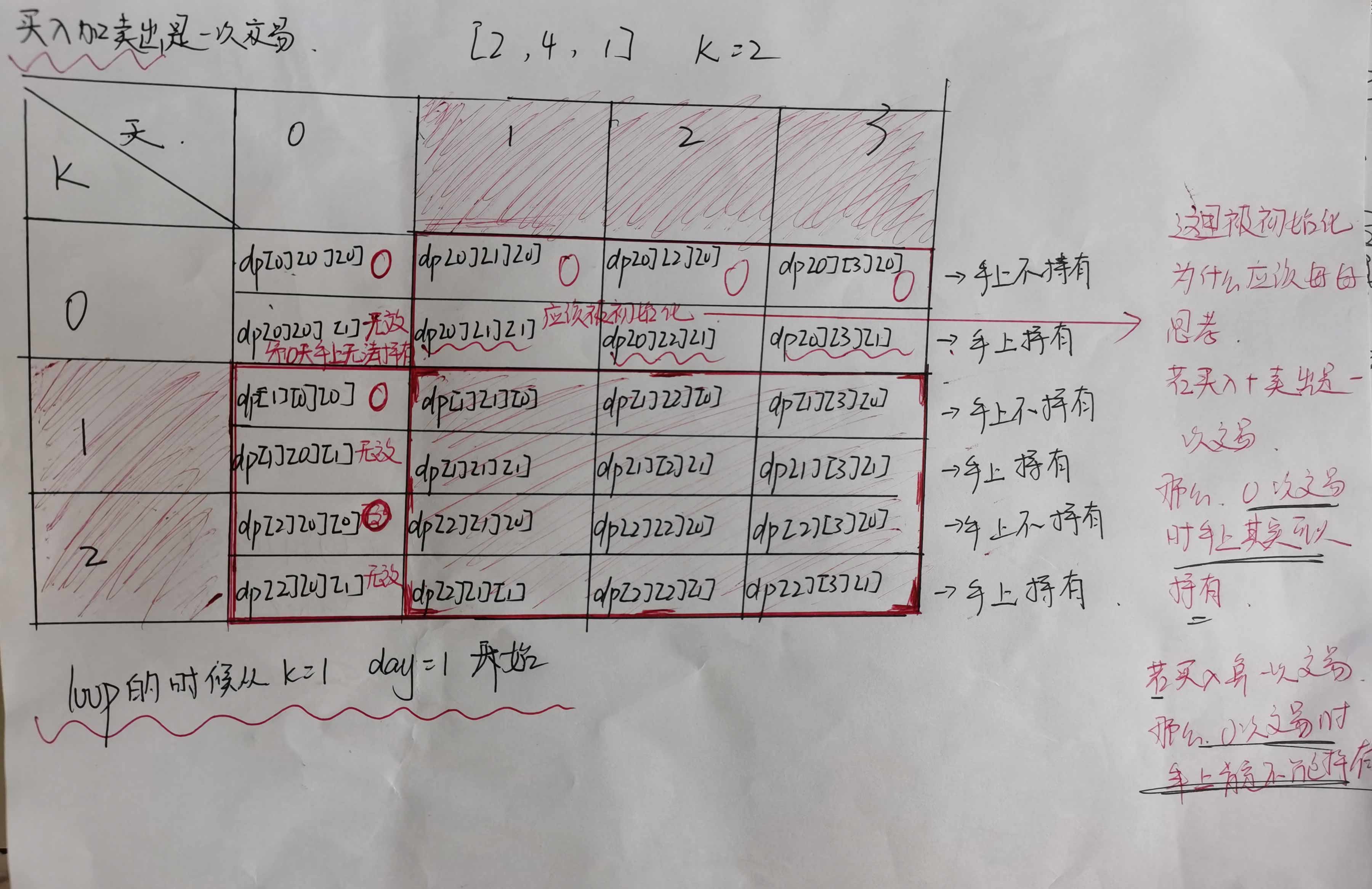
建立三维的数组：dp[k][i][2]
其中k表示的是交易次数，i表示的是第几天，2表示的是有两种状态：手上没有股票/手上有股票
dp[k][i][0] 数组中的数字表示的是到了第i天，交易了k次，手上没有股票获得的最大利益
dp[k][i][1] 数组中的数字表示的是到了第i天，交易了k次，手上持有股票获得的最大利益
在我们写转移方程之前我们还要先考虑之前提出来的问题—交易数怎么算，买+卖是一次交易，我的t表示的是交易次数，那我到底是买入的时候t要加一了，还是卖出的时候t才加一？

答：都可以，不同的定义就会有不同的实现

来看一下两者有什么不同
1>买入就算一次交易：
i天t次交易现在手上不持有 = max(i-1天t次交易手上不持有，i-1天t次交易手上持有 + i天卖出价格prices)
dp[t][i][0] = max(dp[t][i - 1][0], dp[t][i - 1] + prices[i]);

i天t次交易现在手上持有 = max(i-1天t次交易手上持有，i-1天t-1次交易手上不持有 - i天买入价格)
dp[t][i][1] = max(dp[t][i - 1][1], dp[t - 1][i - 1][0] - prices[i])

2>买入后卖出才算一次交易
i天t次交易现在手上不持有 = max(i天t次交易手上不持有，i - 1天t - 1次交易 + i天卖出)
dp[t][i][0] = max(dp[t][i][0], dp[t - 1][i - 1][1] + prices[i])

i天t次交易现在手上持有 = max(i天t次交易现在手上持有，i - 1天t次交易 + i天买入)
dp[t][i][1] = max(dp[t][i][1], dp[t][i - 1][0] - prices[i])

除了转移方程不一样以外，还有初始状态不一样
1>买入就算一次交易：
dp[t][0][0] 0天t次交易，手上不持有：可能的 0
dp[t][0][1] 0天t次交易，手上持有：不可能（0天没有股票，所以无法买入持有;持有说明至少进行了一次买入，买入就交易，因此这里不可能【不可能意思就是不能从这里转移】
dp[0][i][0] i天0次交易，手上不持有：0
dp[0][i][1] i天0次交易，手上持有：不可能（不交易手上不可能持有）

class Solution {
public:
   int maxProfit(int k, vector<int>& prices) {
       if(!prices.size()) return 0;
       if(k >= prices.size()/2)
       {
           int sum = 0;
           for(int i = 1; i < prices.size(); i++)
           {
               int val = prices[i] - prices[i - 1];
               sum += (val > 0? val: 0);
           }
           return sum;
       }
       vector<vector<vector<int>>> dp(k + 1, vector<vector<int>>(prices.size() + 1, vector<int>(2, 0)));
       for(int t = 0; t <= k; t++)
           dp[t][0][1] = -1000000;
       for(int i = 0; i < prices.size(); i++)
           dp[0][i][1] = -1000000;
       for(int t = 1; t <= k; t++)
       {
           for(int i = 1; i <= prices.size(); i++)
           {
               dp[t][i][0] = max(dp[t][i - 1][0], dp[t][i - 1][1] + prices[i - 1]);
               dp[t][i][1] = max(dp[t][i - 1][1], dp[t - 1][i - 1][0] - prices[i - 1]);
           }
       }
       return dp[k][prices.size()][0];
   }
};

2>买入后卖出才算一次交易：
dp[t][0][0] 0天t次交易，手上不持有: 0
dp[t][0][1] 0天t次交易，手上持有: 不可能(0天没有股票，所以无法买入持有) 【如果这里不这样初始化，而是初始化为0，那么我t次交易的无法去做max,max它会取这个0,而不会去取那些负值】
dp[0][i][0] i天0次交易，手上不持有：0
dp[0][i][1] i天0次交易，手上持有：有效的 max(-prices)
dp[0][i][1] = max(dp[0][i - 1][1], -prices[i])

class Solution {
public:
   int maxProfit(int k, vector<int>& prices) {
       if(!prices.size()) return 0;
       if(k >= prices.size()/2)
       {
           int sum = 0;
           for(int i = 1; i < prices.size(); i++)
           {
               int val = prices[i] - prices[i - 1];
               sum += (val > 0? val: 0);
           }
           return sum;
       }
       vector<vector<vector<int>>> dp(k + 1, vector<vector<int>>(prices.size() + 1, vector<int>(2, 0)));
       for(int t = 0; t <= k; t++)
       {
           dp[t][0][1] = -1000000;
       }

       dp[0][1][1] = -prices[0];
       for(int i = 2; i <= prices.size(); i++)
           dp[0][i][1] = max(dp[0][i - 1][1], -prices[i - 1]);
       for(int t = 1; t <= k; t++)
       {
           for(int i = 1; i <= prices.size(); i++)
           {
               dp[t][i][0] = max(dp[t][i - 1][0], dp[t - 1][i - 1][1] + prices[i - 1]);
               dp[t][i][1] = max(dp[t][i - 1][1], dp[t][i - 1][0] - prices[i - 1]);

           }
       }
       return dp[k][prices.size()][0];
   }
};

二维数组的解法
如果说我们把一次买/一次卖都当是一次交易，那么总的交易数字是2*k，0表示没有交易,0天代表没有股票
dp[0][0] = 0 0天么有交易，钱最大是0
dp[t][0] 当是第0天的时候，t(t>=1)次交易，第0天没有交易，所以是-100000
【这里初始化后，下面这里才是正确的，如果不初始化为-1000000，初始化为0，t = 1 那么这里相当于不会买入dp[t][i] = max(dp[t - 1][i - 1] - prices[i - 1], dp[t][i - 1]) 】

class Solution {
public:
   int maxProfit(int k, vector<int>& prices) {
       if(!prices.size()) return 0;
       if(k >= prices.size()/2)
       {
           int sum = 0;
           for(int i = 1; i < prices.size(); i++)
           {
               int val = prices[i] - prices[i - 1];
               sum += (val > 0? val: 0);
           }
           return sum;
       }
       vector<vector<int>> dp(k * 2 + 1, vector<int>(prices.size() + 1, 0));
       for(int t = 1; t <= 2 * k; t += 2)
           dp[t][0] = -1000000;
       for(int t = 1; t <= 2 * k; t++)
       {
           for(int i = 1; i <= prices.size(); i++)
           {
               if(t%2 == 1)//买入
               {
                   dp[t][i] = max(dp[t - 1][i - 1] - prices[i - 1], dp[t][i - 1]);
               }
               else//卖出
               {
                   dp[t][i] = max(dp[t - 1][i - 1] + prices[i - 1], dp[t][i - 1]);
               }
           }
       }
       return dp[k * 2][prices.size()];
   }
};

还有一种思路：
dp[t][i] i天,最多t次交易完成后，最大利润
转移方程
i天,最多t次交易完成后，最大利润 = max(i-1天已经交易了t次， j - 1天已经交易t -1次 + prices[i] - prices[j])

class Solution {
public:
   int maxProfit(int k, vector<int>& prices) {
       if(!prices.size()) return 0;
       if(k >= prices.size()/2)
       {
           int maxsumval = 0;
           for(int i = 1; i < prices.size(); i++)
               if(prices[i] > prices[i - 1])
                   maxsumval += prices[i] - prices[i - 1];
           return maxsumval;
       }
       vector<vector<int>> dp(k + 1, vector<int>(prices.size() + 1, 0));
       for(int t = 1; t <= k; t++)
       {
           for(int i = 1; i < prices.size(); i++)
           {
               int val = 0;
               for(int j = 0; j <= i; j++)
               {
                   val = max(val, prices[i] - prices[j] + dp[t - 1][j]);
               }
               dp[t][i] = max(dp[t][i - 1], val);
           }
       }
       return dp[k][prices.size() - 1];
   }
};

优化之后

class Solution {
public:
   int maxProfit(int k, vector<int>& prices) {
       if(!prices.size()) return 0;
       if(k >= prices.size()/2)
       {
           int maxsumval = 0;
           for(int i = 1; i < prices.size(); i++)
               if(prices[i] > prices[i - 1])
                   maxsumval += prices[i] - prices[i - 1];
           return maxsumval;
       }
       vector<vector<int>> dp(k + 1, vector<int>(prices.size() + 1, 0));
       vector<int> v(k + 1, prices[0]);
       for(int i = 1; i < prices.size(); i++)
       {
           for(int t = 1; t <= k; t++)
           {
               v[t] = min(v[t], prices[i] - dp[t - 1][i - 1]);
               dp[t][i] = max(dp[t][i - 1], prices[i] - v[t]);  
           }
       }
       return dp[k][prices.size() - 1];
   }
};

一维数组

class Solution {
public:
   int maxProfit(int k, vector<int>& prices) {
       if(!prices.size()) return 0;
       if(k >= prices.size()/2)
       {
           int maxsumval = 0;
           for(int i = 1; i < prices.size(); i++)
               if(prices[i] > prices[i - 1])
                   maxsumval += prices[i] - prices[i - 1];
           return maxsumval;
       }
       vector<int> dp(k + 1, 0);
       vector<int> v(k + 1, prices[0]);
       for(int i = 1; i < prices.size(); i++)
       {
           for(int t = 1; t <= k; t++)
           {
               v[t] = min(v[t], prices[i] - dp[t - 1]);
               dp[t] = max(dp[t], prices[i] - v[t]);  
           }
       }
       return dp[k];
   }
};

第二次写题

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if(prices.size() <= k/2)
        {
            int profit = 0;
            for(int i = 1; i < prices.size(); i++)
                if(prices[i] > prices[i - 1])
                    profit += prices[i] - prices[i - 1];
            return profit;
        }
        //如果买入就算一次交易
        vector<vector<vector<int>>> dp = vector<vector<vector<int>>>(k + 1, vector<vector<int>>(prices.size() + 1, vector<int>(2, 0)));
        for(int i = 0; i <= k; i++)
            dp[i][0][1] = -10000;
        for(int i = 1; i <= prices.size(); i++)
            dp[0][i][1] = -10000;
        for(int i = 1; i <= k; i++)
        {
            for(int j = 1; j <= prices.size(); j++)
            {
                dp[i][j][0] = max(dp[i][j - 1][0], dp[i][j - 1][1] + prices[j - 1]);
                dp[i][j][1] = max(dp[i][j - 1][1], dp[i - 1][j - 1][0] - prices[j - 1]);
            }
        }
        return dp[k][prices.size()][0];
    }
};

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if(prices.size() <= k/2)
        {
            int iProfit = 0;
            for(int iDay = 1; iDay < prices.size(); iDay++)
            {
                if(prices[iDay] > prices[iDay - 1])
                    iProfit += prices[iDay] - prices[iDay - 1];
            }
            return iProfit;
        }
        //买入卖出才算一次交易
        vector<vector<vector<int>>> aProfit = vector<vector<vector<int>>>(k + 1, vector<vector<int>>(prices.size() + 1, vector<int>(2, 0)));
        for(int iTimes = 0; iTimes <= k; iTimes++)
            aProfit[iTimes][0][1] = -100000;
        for(int iDay = 1; iDay <= prices.size(); iDay++)
        {
            aProfit[0][iDay][1] = max(aProfit[0][iDay - 1][1], -prices[iDay - 1]);
            // cout<< iDay << " " << aProfit[0][iDay][1] << endl;
        }
        for(int iTimes = 1; iTimes <= k; iTimes++)
        {
            for(int iDay = 1; iDay <= prices.size(); iDay++)
            {
                aProfit[iTimes][iDay][0] = max(aProfit[iTimes][iDay - 1][0], aProfit[iTimes - 1][iDay - 1][1] + prices[iDay - 1]);
                aProfit[iTimes][iDay][1] = max(aProfit[iTimes][iDay - 1][1], aProfit[iTimes][iDay - 1][0] - prices[iDay - 1]);
            }
        }
        return aProfit[k][prices.size()][0];
    }
};

上面两种写法要注意的是，首先因为两层的Loop是从交易次数等于1开始的，所以交易次数为0的时候就需要先赋值了。为什么交易次数为0的要先赋值，这相当于初始条件。而对于买入算一次交易还是卖出才算一次交易两种定义方式的不同，又会导致初始状态的不同，也就是交易次数为0的时候的状态值的不同。同样是转移，但是转移方程不同。
让我们来仔细看一下这个转移的方程。

一次买入或者一次卖出算一次交易

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if(prices.size() <= k/2)
        {
            int iProfit = 0;
            for(int iDay = 1; iDay < prices.size(); iDay++)
            {
                iProfit += (prices[iDay] > prices[iDay - 1])?(prices[iDay] - prices[iDay - 1]):0;
            }
            return iProfit;
        }
        vector<vector<int>> aProfit = vector<vector<int>>(2 * k + 1, vector<int>(prices.size() + 1, 0));
        for(int iTimes = 1; iTimes <= 2 * k; iTimes += 2)
            aProfit[iTimes][0] = -10000;
        for(int iTimes = 1; iTimes <= 2 * k; iTimes++)
        {
            for(int iDay = 1; iDay <= prices.size(); iDay++)
            {
                if(iTimes % 2 == 1)//买入
                    aProfit[iTimes][iDay] = max(aProfit[iTimes][iDay - 1], aProfit[iTimes - 1][iDay] - prices[iDay - 1]);
                else//卖出
                    aProfit[iTimes][iDay] = max(aProfit[iTimes][iDay - 1], aProfit[iTimes - 1][iDay] + prices[iDay - 1]);
            }
        }
        return aProfit[2 * k][prices.size()];
    }
};

第三次写题

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        vector<vector<vector<int>>> aProfit = vector<vector<vector<int>>>(k + 1, vector<vector<int>>(prices.size() + 1, vector<int>(2, 0)));
        if(prices.size() <= k/2)
        {
            int iProfit = 0;
            for(int i = 1; i < prices.size(); i++)
            {
                if(prices[i - 1] < prices[i])
                    iProfit += (prices[i] - prices[i - 1]);
            }
            return iProfit;
        }
        //买入加卖出是一次交易
        for(int i = 0; i <= k; i++)
            aProfit[i][0][1] = -10000;

        for(int i = 1; i <= prices.size(); i++)
            aProfit[0][i][1] = max(aProfit[0][i- 1][1], -prices[i - 1]);

        for(int i = 1; i <= k; i++)
        {
            for(int j = 1; j <= prices.size(); j++)
            {
                aProfit[i][j][0] = max(aProfit[i][j - 1][0], aProfit[i - 1][j - 1][1] + prices[j - 1]);
                aProfit[i][j][1] = max(aProfit[i][j - 1][1], aProfit[i][j - 1][0] - prices[j - 1]);
            }
        }
        return aProfit[k][prices.size()][0];
    }
};

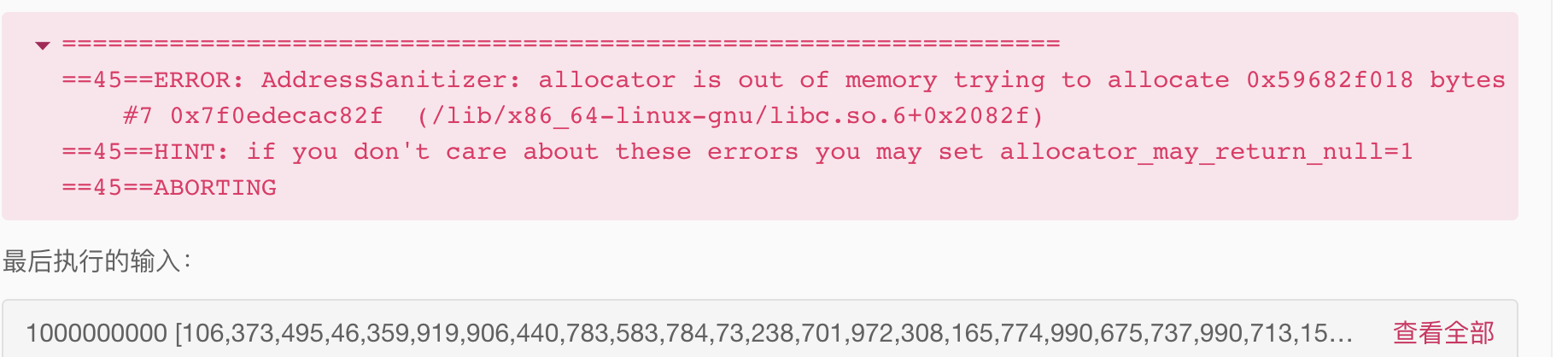
修改后

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if(prices.size() <= k/2)
        {
            int iProfit = 0;
            for(int i = 1; i < prices.size(); i++)
            {
                if(prices[i - 1] < prices[i])
                    iProfit += (prices[i] - prices[i - 1]);
            }
            return iProfit;
        }
        vector<vector<vector<int>>> aProfit = vector<vector<vector<int>>>(k + 1, vector<vector<int>>(prices.size() + 1, vector<int>(2, 0)));
        //买入加卖出是一次交易
        for(int i = 0; i <= k; i++)
            aProfit[i][0][1] = -10000;

        for(int i = 1; i <= prices.size(); i++)
            aProfit[0][i][1] = max(aProfit[0][i - 1][1], -prices[i - 1]);

        for(int i = 1; i <= k; i++)
        {
            for(int j = 1; j <= prices.size(); j++)
            {
                aProfit[i][j][0] = max(aProfit[i][j - 1][0], aProfit[i - 1][j - 1][1] + prices[j - 1]);
                aProfit[i][j][1] = max(aProfit[i][j - 1][1], aProfit[i][j - 1][0] - prices[j - 1]);
            }
        }
        return aProfit[k][prices.size()][0];
    }
};