取反 ~ (NOT)
取反运算的符号是 ~,就是将 0 转为 1,将 1 转为 0 的操作,以 32 位整数 22 为例进行取反,首先将 22 转为二进制 00000000 00000000 00000000 00010110,再进行取反操作就是把 1 改为 0,0 改为 1,所以 ~22 的取反结果为 11111111 11111111 11111111 11101001
负数**
负数与正数属于有符号的的二进制,其区别在于高位是否为 1,负数的高位全部为 1,而正数的高位全部为 0,这里需要引入补码的概念,有符号的二进制是以补码形式存在,正数的补码与原码一致,而负数的补码,最高位是 1,取反后加 1 得到。
+22 的补码是 00000000 00000000 00000000 00010110
-22 的补码是将 +22 取反后得到 11111111 11111111 11111111 11101001 再加 1,最终结果为 11111111 11111111 11111111 11101010,所以,我们也可以得出公式 -22 = ~22 + 1,同时也得到 ~22 = -22 - 1 = -23
如果我们得到的是一个补码(通过最高位判断正负)如何计算他的十进制数值呢?
最高位为 0 表示正数,如补码 00000000 00000000 00000000 00010110 转为十进制就是 22
最高位为 1 表示负数,如补码 11111111 11111111 11111111 11101010,我们同样的需要取反后加 1 得到正数后加上负号即可。
~ 11111111 11111111 11111111 11101010-------------------------------------00000000 00000000 00000000 00010101+ 1-------------------------------------00000000 00000000 00000000 00010110 (十进制 22)22 再加上负号,最终结果为 -22
那么,如果我们要将一个正数转为负数的二进制又该怎么处理呢?同样的,可以通过取反再加一计算,过程如下。
~ 00000000 00000000 00000000 00010110
-------------------------------------
11111111 11111111 11111111 11101001
+ 1
-------------------------------------
11111111 11111111 11111111 11101010 (十进制 -22)
与 & (AND)
与运算的符号是 &,反映到二进制的表达式为:1&1 = 1 1&0 = 0&1 = 0&0 = 0
对 a = 1011(十进制 11),b = 0110(十进制 6)进行与运算的过程如下。
a & b = 1011 & 0110
1011
& 0110
------
0010 (十进制 2)
或 | (OR)
或运算的符号是 |, 反映到二进制的表达式为:1|1 = 1|0 = 0|1 = 1 0|0 = 0
对 a = 1011(十进制 11),b = 0110(十进制 6)进行或运算的过程如下。
a | b = 1011 | 0110
1011
| 0110
------
1111 (十进制 15)
异或 ^ (XOR)
异或运算的符号是 ^, 反映到二进制的表达式为:1^1 = 0^0 = 0 1^0 = 0^1 = 1
对 a = 1011(十进制 11),b = 0110(十进制 6)进行异或运算的过程如下。
a ^ b = 1011 ^ 0110
1011
^ 0110
------
1101 (十进制 13)
左移 (<<)
左移表示将二进制向左边移动,并在最低位补 0,以 +11(二进制 1011)为例,+11 << 1 左移一位就变成 22(二进制 10110)。另外,左移一位等价于乘以 2,左移 n 位等价于乘以 ,当然这是基于不溢出的前提下。
再以负数 -11(二进制 11111111 11111111 11111111 11110101)为例,-11 << 1 左移一位后变成
11111111 11111111 11111111 11101010,通过取反加一后得到的是 -22,看来正负数的左移都可以表示乘以 ,当然还是基于不溢出的前提下。
右移 (>>)
右移表示将二进制向右边移动,准确来说是带符号右移,正数在最高位补 0,负数在最高位补 1,以 +11(二进制 1011)为例,+11 >> 1 右移一位就变成 +5(二进制 0101)。另外,根据左移乘 2 的经验,我们很容易联想到右移一位等价于除以 2,但只是后忽略了浮点数,左移 n 位等价于除以 但只是后忽略了浮点数。
刚才是 +11 作为例子右移一位,现在以 -11 (二进制 11111111 11111111 11111111 11110101) 为例,-11 >> 1 右移一位后变成 11111111 11111111 11111111 11111010,通过取反加一后得到的是 -6,所以右移除 2 对于负数不成立。
无符号右移 (>>>)
无符号右移与右移相似,但无符号右移的高位始终补 0,忽略正负数,以 -11(二进制 11111111 11111111 11111111 11110101)为例,无符号右移一位得到的是 2147483642(二进制 01111111 11111111 11111111 1111010),由于最高位变为 0,所以 -11 >>> 1 后变为正数。
实现基本运算
位运算实现加法
加法运算是利用 XOR 处理非进位相加,利用 AND 处理进位,以 +11 (1011) 和 +6 (0110) 为例,利用位运算实现加法的过程如下。
- 先通过 XOR 进行运算
- 再通过 AND 操作后左移一位实现进位效果
- 最后将 #1 和 #2 的结果再一次通过 XOR 运算,重复 #1 和 #2 的过程,直到 #2 的进位为 0 停止
- 完整过程如下 ```java 1011 (十进制 +11) ^ 0110 (十进制 +6)
1101 (记作 a)
1011 (十进制 +11)
& 0110 (十进制 +6)
0010
0010 << 1
0100 (记作 b)
```java
1101 (a 值)
^ 0100 (b 值)
------
1001 (记作 c)
1101
& 0100
------
0100
0100 << 1
------
1000 (记作 d)
1001 (c 值)
^ 1000 (d 值)
------
0001 (记作 e)
1001
& 1000
------
1000
1000 << 1
------
10000 (记作 f)
00001 (e 值)
^ 10000 (f 值)
-------
10001 (记作 g,十进制 17)
00001
& 10000
-------
00000 (进位为 0 停止,返回 g 值)
找到了规律后,再通过代码实现就变得简单了,实现如下,代码也非常精简。
public int add(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
对于上面这段代码,还可以更加精简,现在我们尝试利用已经运算好的 a = a ^ b 作为值计算出 carray(进位)数,假设 a = 1011(十进制 11),b = 0110(十进制 6)。
// a = 1011, b = 0110
a = a ^ b; // 1011 ^ 0110 = 1101
// a = 1101, b = 0110
b = a ^ b; // 1101 ^ 0110 = 1011 这个就是原来 a 的值
发现通过两次 XOR 运算之后结果还是原来 a 的值,相当于 a == (a ^ b) ^ b,因此可以作如下化简。
public int add(int a, int b) {
while (b != 0) {
a = a ^ b;
b = ((a ^ b) & b) << 1;
}
return a;
}
其实还能更加简短,如下代码所示,但越是简短就越难维护和理解,因此还是推荐第一个写法。
public int add(int a, int b) {
while ((b = (((a = a ^ b) ^ b) & b) << 1) != 0);
return a;
}
如果明白了位运算实现加法,建议到 leetcode 自行实现一遍,对应 leetcode 第 371 题,虽然标识为 Easy 级别,但思考过程,我以为已经是 Hard 级别了,链接为:https://leetcode.com/problems/sum-of-two-integers/
还有一种是利用递归方式实现,代码如下,不需要其他技巧,实现上就非常简洁,不过需要用到栈,为了避免超出最大的栈深度,所以 Java 中的类库基本上都是使用迭代实现。
public int add(int a, int b) {
return b == 0 ? a : add(a ^ b, (a & b) << 1);
}
位运算实现减法
有了加法基础,我们就可以利用到减法算术中,如 11 - 6 通过加法可转为 11 + (-6) 来表示,上面我们提到负数就是取反后再加一计算得到,所以 -6 可以通过 ~6 + 1 来表示。
public int add(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
public int subtract(int a, int b) {
return add(a, add(~b, 1));
}
位运算实现乘法
通过学习减法是如何通过加法实现之后,对于乘法,我想你可能已经想到,m x n 就是 n 个 m 相加或 m 个 n 相加就可以得到了。
public int add(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
public int multiply(int a, int b) {
int c = a <= 0 ? a : add(~a, 1); // 转为负正数处理
int d = b <= 0 ? b : add(~b, 1); // 转为负正数处理
int sum = 0;
for (int i = 0; i < d && i <= 0; i = subtract(i, 1)) {
sum = add(sum, c);
}
return (a ^ b) >= 0 ? -sum : sum; // 注意 sum 为负整数
}
注意参数 b 转为负整数处理了,这是因为负整数的绝对值要比真正数的绝对值要大,避免溢出问题,因此统一以负整数处理。虽然上面的代码可以运行,但效率实在有点太低了,如果参数 b 较大,则遍历的时间就会增加,有无更高效的方法呢?我们不妨参考十进制的乘法是怎么实现的?能否引用到二进制的乘法中呢?通过下面这个例子,我们进行简单的推理和验证。
15 01111 a
x 22 x 10110 b
---- ----------
30 00000
30 01111
---- 01111
330 00000
01111
----------
101001010 (对应十进制 330)
01001010 计算后的十进制为 330,看来二进制的乘法也可以用十进制的乘法来运算,那么我们翻译成如下代码。
public int multiply(int a, int b) {
if (a == 0)
return 0;
int sum = 0;
while (b != 0) {
if ((b & 1) == 1)
sum = add(sum, a);
a <<= 1;
b >>>= 1;
}
return sum;
}
如果参数 b 的最低位为 1,则将参数 a 与 参数 b 相加,再将参数 a 左移一位,参数 b 右移一位,重复这个过程,直到参数 b 为零。
注意 a 或 b 等于 0 的情况,虽然迭代中已经可以处理 a 或 b 等于 0 的情况,但为了让程序更加有效率,我们可以提前处理。可能你也发现了 b >>>= 1 使用到了无符号右移,无符号右移可以使得参数 b 右移后高位补零,如果使用的是 b >>= 1 带符号右移,b 为负数时,则高位只会补一,从而导致循环无法退出。
位运算实现除法
除法与乘法相似,可对应减法,通过重复调用减法运算直到被除数为 0,但效率也是非常低下,代码如下,同样的为了避免溢出,统一以负整数处理。
public int add(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
public int subtract(int a, int b) {
return add(a, add(~b, 1));
}
public int divide(int a, int b) {
int c = a <= 0 ? a : add(~a, 1); // 转为负正数处理
int d = b <= 0 ? b : add(~b, 1); // 转为负正数处理
int quotient = 0;
for (int i = c; i <= d && i <= 0; i = subtract(i, d)) {
c = subtract(c, d);
quotient = add(quotient, 1);
}
return (a ^ b) >= 0 ? quotient : -quotient;
}
与十进制除法一样,二进制也是可以通过竖式除法运算得到,相对于十进制,二进制其实更加简单,因为只有 0 或 1 两个选择,但十进制存在 0 到 9 十个选择。同样的,我们来验证一下,利用乘法运算的 15 x 22 = 330,通过二进制的 330 除以二进制的 15,观察是否能够得到二进制的 22
101001010 ÷ 01111 = 10110
330 ÷ 15 = 22
通过上面这个例子看来也是可行的,再将其翻译成代码你会发现,由于负整数高位全为 1 的原因,这个竖式计算只能适应正整数,或者你会想通过将负整数转为正数再计算。貌似也是可以的,只不过 Integer.MIN_VALUE 要比 Integer.MAX_VALUE 的绝对值要大 1,也就是说将 Integer.MIN_VALUE 尝试转为正整数就会存在溢出的问题,|Integer.MIN_VALUE| = Integer.MIN_VALUE。
换一个思路,不通过数学思维解决,我们可以通过算法思维重新思考问题,既然负整数转正整数,那我们全部都只操作负数,最后再将符号转回来即可。
算法思路
- 通过二分法,也就是分治的思想,将除数不断乘以 2,即不断左移一位,直到最后一个小于被除数的值
- 被除数减去 #1 部分的结果,再将剩余的数作为被除数重复 #1 和 #2 的步骤,直到被除数小于除数
- 最后将乘以 2 倍数相加即可得到结果
为了让这个过程更加清晰,下图以被除数是 167,除数是 3 为例的计算过程
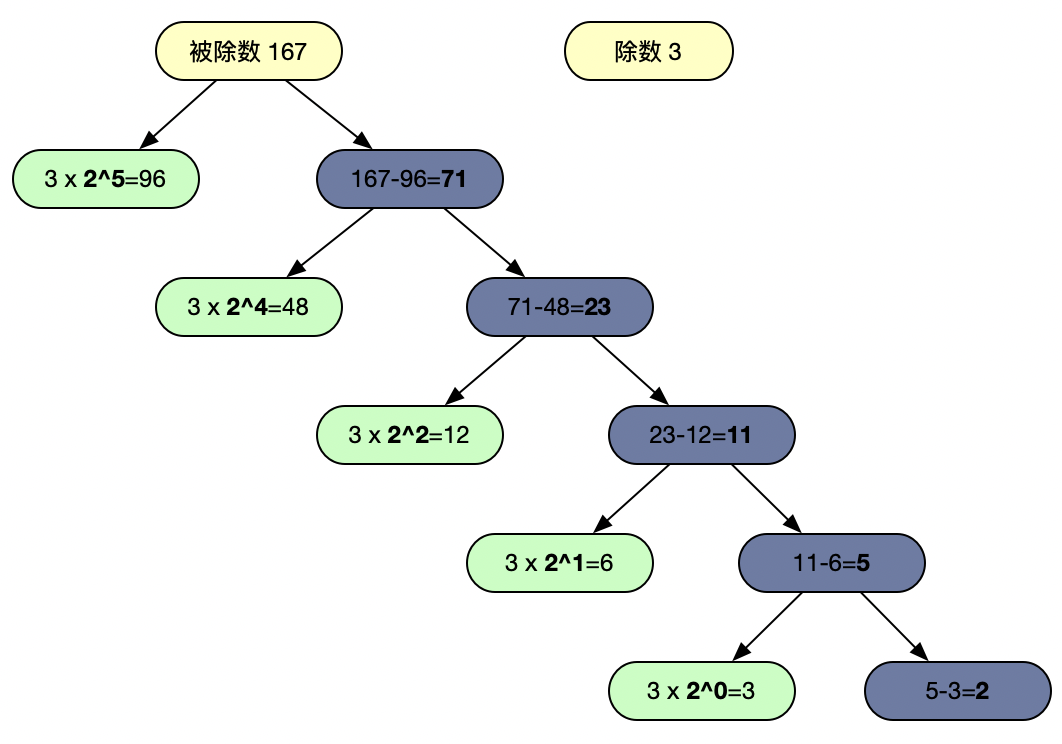
将绿色部分的加粗数字相加则是最终结果,上图的最终结果为
而值得一提的是最后的 就是
取模的值。当然,这里仅能处理整数,如果加上浮点数就会更加复杂,这里就不展开了,有兴趣的读者可以自行实现。
public int divide(int dividend, int divisor) {
// 处理溢出问题
if (dividend == Integer.MIN_VALUE && divisor == -1)
return Integer.MAX_VALUE;
int end = dividend <= 0 ? dividend : add(~dividend, 1);
int sor = divisor <= 0 ? divisor : add(~divisor, 1);
int res = div(end, sor);
return (dividend ^ divisor) >= 0 ? res : -res;
}
public int div(int dividend, int divisor) {
if (dividend > divisor) return 0;
int sum = divisor, count = 1;
while (dividend <= (sum << 1) && (sum << 1) < 0) {
sum <<= 1;
count <<= 1;
}
return add(count, div(subtract(dividend, sum), divisor));
}
public int subtract(int a, int b) {
return add(a, add(~b, 1));
}
public int add(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
循环的实现方式如下。
public int divide(int dividend, int divisor) {
// 处理溢出问题
if (dividend == Integer.MIN_VALUE && divisor == -1)
return Integer.MAX_VALUE;
int end = dividend <= 0 ? dividend : add(~dividend, 1);
int sor = divisor <= 0 ? divisor : add(~divisor, 1);
int quotient = 0;
while (end <= sor) {
int sum = sor;
int count = 1;
while ((sum << 1) >= end && (sum << 1) < 0) {
sum <<= 1;
count <<= 1;
}
end = subtract(end, sum);
quotient = add(quotient, count);
}
return (dividend ^ divisor) >= 0 ? quotient : add(~quotient, 1);
}

