1. 图的简介

生活中，我们对于图再熟悉不过了。到动物公园，我们购票时就会携带一张地图进园。开车时，我们打开导航地图出发想去的地方，还有我们常用的微信，记录着朋友之间的关系。我们都知道图的作用如此广泛，但是否考虑过在计算机的内存中如何保存图这种数据结构呢？而图又有哪些种类呢？

2. 图的类型

在计算机的世界里，聪明的工程师将图抽象为无向图、无向权重图、有向图、有向权重图。

我们日常使用的微信中记录的好友关系则可以使用无向图表示；如果有玩过王者荣耀，则对游戏中的好友之间的亲密度不陌生，好友关系及亲密度则可以使用无向权重图表示；还有我们的微博和现在使用的语雀中的关注功能表示两个用户的单向关系则可以使用有向图表示；如果你有一部手机，那么必不可少的就是导航软件，其中的地图就可以使用使用有向图权重图表示两个地点的方向和两个地点的距离。

为了有个更直观的感受，请观察图 1 中分别表示的无向图、无向权重图、有向图、有向权重图。

图 1
_
图中的节点我们称为顶点(Vertex)其缩写为 V，边(Edge)缩写为 E。另外，顶点和边还有一个概念叫度(degree)表示一个顶点相邻边数，而有向图中如果存在顶点 A 有一条指向顶点 B 的边，则对于顶点 B 这条边称为入度(indegree)，相反的，对于顶点 A 这条边则称为出度(outdegree)。

3. 图的表示方法

清楚了图的样子，我们再来看看如何在内存中表示无向图、无向权重图、有向图和有向权重图，每一种表示方法都有其优缺点，实际使用时按需选择存储方式。

3.1. 边列表(Edge Lists)

顾名思义，是通过一条边记录相邻两个顶点，两个顶点的关系以一个数组表示，具体可参考下图 2。


图 2_

我们可以看到第二维数据的最大长度为 3，数组中的最后一位表示权重，这好比 X/Y 轴中的坐标位置。同时为了减少冗余，无向图可理解为双向图，如 [0,1] 无需再新增 [1,0] 表示。

边列表优点是节省空间，但缺点是不够直观，可能你已经发现，无向图和有向图的表示方式其实存在冲突，因此边列表的无法很好的表达出图的方向。那么你可能会说，无向图中我们只要反向增加顶点之间的关系就可以了，不得不说这确实是一个非常有效的补充，如下所示。

[
  [0, 1],[1, 0],
  [0, 2],[2, 0],
  [0, 3],[3, 0],
  [2, 3],[3, 2],
  [1, 4],[4, 1],
  [3, 4],[4, 3]
]

如果你还接触过数据库，并对数据库表的一对多及多对多有过设计，边列表的表示方式就相当于中间表记录着用户表的两个主键。

到现在，一切都很好，边列表非常节省内存空间，不过一旦你的程序中获取的是边列表这种储存结构，一定非常难受，这是因为当你将要计算一个顶点的度数(边数)或获取该顶点对应出度的所有顶点的时候，则需要遍历整个数组，无向图的时间复杂度为 O(2*E) (E 为边的个数)。

3.2. 邻接矩阵(Adjacency Matrices)

为了解决边列表的表现力不足及查询效率低下的问题，我们再看另一种表示方式-邻接矩阵，通过一个二维数组及数组位置的方式表示相邻两个顶点之间的关系。具体可参考下图 3。


图 3

我们现在再来计算一个顶点度数(边数)或获取该顶点对应出度的所有顶点，只要遍历一行的数据获取非 0 的列即可，时间复杂度为 O(V)(V 为顶点个数)。

邻接矩阵的优点是查找快捷，如果给定一个 edge(i,j) 的边，则可直接在矩阵中通过 graph[i][j] 查询。直观且表现力强，无向图中为 1 的数字总是对称，而对于无向权重图则是非 0 的数字总是对称。

而邻接矩阵的缺点是在矩阵中存在较多的值为 0 的元素时，这些多余元素的存在明显占据着额外的内存，这对于稀疏图来说十分不友好。大部分情况下，查询顶点相邻边顶点的效率都不高，试想一下如果顶点以英文字母表示，那如果要计算一个顶点度数(边数)或获取该顶点对应出度的所有顶点就需要遍历所有的行和列，时间复杂度就从 O(V) 变成了 O(V)。

3.3. 邻接表(Adjacency Lists)

由于边列表和邻接矩阵存在各种各样的不足，那么是否存在一种表示方式能够既省空间且计算和查询速度更快呢？这个就是接下来要说的邻接表，这是一个散列表(数组)加链表的方式保存相邻顶点之间关系的表示方式，具体可参考下图 4。


图 4

现在再来计算一个顶点度数(边数)或获取该顶点对应出度的所有顶点，首先需要说明的是散列表查询一个顶点的时间复杂度是 O(1)，我们发现度数就是链表的长度，所以时间复杂度是 O(1)，获取出度的所有顶点，其时间复杂度是 O(D)，D 为顶点的度数(degree)，值范围是 0 <= D <= V。其空间复杂度又是多少呢？以无向图为例计算，所有顶点需要一个数组记录，且每个顶点对应储存的列表与度(degree)有关，因此需要的空间复杂度为 O(V+D)。

3.4. 逆邻接表(Inverse Adjacency Lists)

邻接表似乎已经很完美了，但我们要是换一个问题，把获取该顶点对应出度的所有顶点改为获取该顶点对应入度的所有顶点。这个时候邻接表就用不上了，如果使用暴力遍历的方式效率也会非常低下，时间复杂度也会变得很高。如果我们把有向图中的出度和入度互换，相当于将方向逆转，以有向权重图为例，参考下图 5 逆邻接表的构造过程。

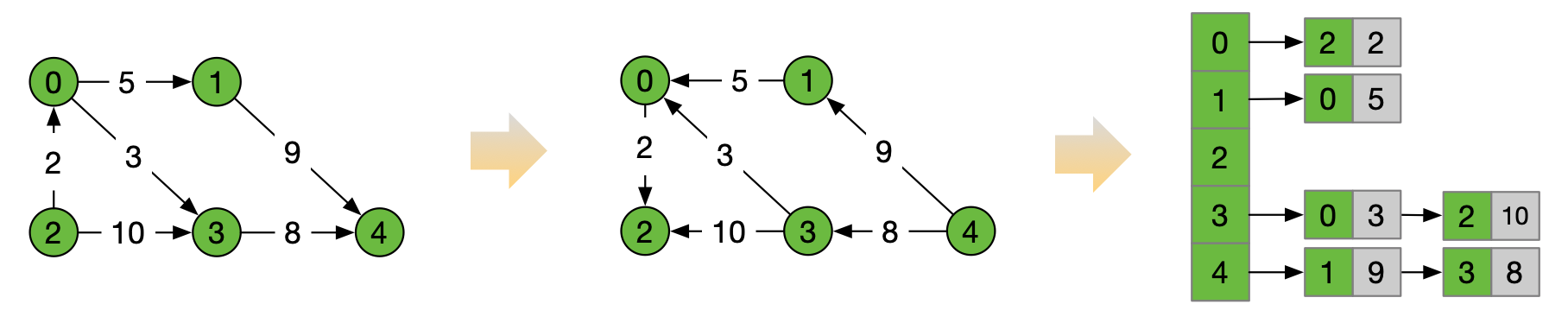
图 5
_
以微博作为实际例子，顶点的出度表示用户关注另一个用户，顶点的入度表示用户被关注，如果邻接表能计算出一个用户关注的所有用户，那逆邻接表就能计算出关注该用户的所有用户。