1. 复杂度介绍

学习算法的第一件事情肯定是学会复杂度分析，尽管复杂度分析不能非常准确的评估出程序的效率及空间消耗，但能够正确的指引我们识别出代码运行效率的高低及空间消耗的多少。
实质上时间复杂度可以理解为操作数，计算时间复杂度和空间复杂度的时候，我们一般会通过大 O 通过忽略系数，以常量级表示，例如，忽略系数则将 O(2n) 表示为 O(n)，常量级则将 O(3) 表示为 O(1)。

2. 时间复杂度

2.1. 最好/最坏/平均

来看一段代码，我们分别来推导它的最好/最坏/平均的时间复杂度。

需求：我们从一个数组中查找一个数，当命中时立即返回该元素在数组中的下标，如果没找到，则返回 -1

int match(int[] arr, int target) {
  for (int i = 0; i < arr.length; i++) {
    if (arr[i] == target) {
      return i;
    }
  }
  return -1;
}

假设 int[] arr 数组参数非空

最好的情况是命中第一个元素并返回，此时的时间复杂度为 O(1)。

最坏的情况是不命中任何元素，此时的时间复杂度为 O(n)。

对于平均时间复杂度，我们以算术平均数来计算，出现在数组中的不同位置就有不同的时间复杂度，即第一个为 O(1) 第二个为 O(2) … 第n个O(n)，如果不存在，那么遍历所有数据的时间复杂度也是 O(n)，由此我们通过算术平均数公式复杂度分析 - 图1 ，当 n 远远大于 3 时，则 3 及 1 都将成为质点，得出 n+3 = n+1，所以约等于 O( 复杂度分析 - 图2 )，再忽略常数则最终结果是 O(n)。

由于命中数组与不命中数组的概率不一致，这类情况我们可以通过加权平均数来计算，但因为概率计算过于复杂就不在这里展开了，至少平均时间复杂度忽略系数后依然是正确的 O(n)。

2.2. 均摊

以 Java 的 ArrayList 为例，现在来分析一下 ArrayList.add 操作的时间复杂度。要知道 ArrayList 的底层数据结构是数组，因此 add 操作将会遇到超出最大容量的情况。以下是 JDK 1.8 的 ArrayList.add 部分源码，为了方便展示，这里将方法内容进行了合并。

public boolean add(E e) {
  if (size + 1 == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
    minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
  }
  modCount++;
  // overflow-conscious code
  if (minCapacity - elementData.length > 0)
    grow(minCapacity);
  elementData[size++] = e;
  return true;
}
private void grow(int minCapacity) {
  // overflow-conscious code
  int oldCapacity = elementData.length;
  int newCapacity = oldCapacity + (oldCapacity >> 1);
  if (newCapacity - minCapacity < 0) newCapacity = minCapacity;
  if (newCapacity - MAX_ARRAY_SIZE > 0) newCapacity = hugeCapacity(minCapacity);
  // minCapacity is usually close to size, so this is a win:
  elementData = Arrays.copyOf(elementData, newCapacity);
}

正常情况下，如果不涉及扩容，直接 elementData[size++] = e 即可完成 add 操作，时间复杂度为 O(1)。

而需要扩容的时间复杂度又是多少呢？通过 int newCapacity = oldCapacity + (oldCapacity >> 1) 可见，自动扩容是以原来长度的 1.5 倍增长，并通过 elementData = Arrays.copyOf(elementData, newCapacity) 将原来的数据迁移到新数组中，这个过程的时间复杂度为 O(n)。

那是否我们就可以认定 ArrayList.add 操作的时间复杂度就是最坏的情况 O(n) 呢？这样评估时间复杂度实在太不公平了，所以我们引入了均摊时间复杂度计算，将扩容的时间分摊到非扩容的时间中，就得出复杂度分析 - 图3 复杂度分析 - 图4 ，当 n 远大于 1 的时候，n+1 ≈ n，因此均摊的时间复杂度就可以认为 O(2)，最终以常量级表示时间复杂度为 O(1)。

2.3. 常见的时间复杂度

如果觉得最好/最坏/平均/均摊的时间复杂度计算比较复杂，那么我们可以只要记住以下几种常见的时间复杂度表示方法即可，分别是 O(1) / O(logN) / O(n) / O(NlogN) / O(n) / O(2) / O(n!)。

O(1)

int i = 3;
int j = 12
int sum = i + j;

O(logN)

int sum = 0;
int i = 1;
while (i < n) {
  sum += i;
  i *= 2;
}

O(n)

int sum = 0;
for (int i = 0; i < n; i++) {
  sum += i;
}

O(nlogn)

int sum = 0;
for (int i = 0; i < n; i++) {
  sum += i;
  for (int j = 0; j < n; j*=2) {
    sum += j;
  }
}

O(n)

x 为 2 的情况下 O(n)

int sum = 0;
for (int i = 0; i < n; i++) {
  for (int j = 0; j < n; j++) {
    sum += (i + j);
  }
}

x 为 3 的情况下 O(n)

int sum = 0;
for (int i = 0; i < n; i++) {
  for (int j = 0; j < n; j++) {
    for (int k = 0; k < n; k++) {
      sum += (i + j + k);
    }
  }
}

如此类推，每增加一个循环，x 就需要加 1。

O(2)

一般出现在回溯算法的实现，假设我们有一组包含大小写的字母，现在，我们需要把这一组字母分别按照不同的大小写展示出来，一共有多少种组合呢？这里我们用到回溯算法，回溯算法在后面将会详细介绍。

String src = "aBdiDoxDS";
char[] chs = src.toCharArray();
int count = 0;
void casePermutation(char[] chs, int i) {
  if (i == chs.length) {
    count++; // 组合数 + 1
  }
  char c = chs[i];
  casePermutation(chs, i + 1); // c 保持不变
  if (isLowerCase(c)) { // 如果 c 是小写，则转为大写
    chs[i] = toUpperCase(c);
    casePermutation(chs, i + 1);
  }
  if (isUpperCase(c)) { // 如果 c 是大写，则转为小写
    chs[i] = toLowerCase(c);
    casePermutation(chs, i + 1);
  }
  chs[i] = c; // 还原
}

casePermutation(chs, 0);
System.out.println(count);

我们对 String src = "aBdiDoxDS" 进行分析，对于每一个字符，均存在两个情况，分别是保持不变及小写转大写或者是大写转小写。

a B d i D o x D S
2 2 2 2 2 2 2 2 2

对每一个字符的情况相乘，则得到时间复杂度为 O(222…2) = O(2)。

O(n!)

其实这类时间复杂度并不常见，也许你还觉得这种时间复杂度的程序至今还没被你发现过，甚至思考，这种复杂度的算法写起来也很困难，接下来，我举一个实际的例子来揭露这种罕见的时间复杂度算法。

现在我们来看一个问题，将 [1,2,3,4,5] 这样一个数组打印出来它的所有不同顺序的组合情况，这就是数学里的排列组合，该数组长度为 5，所以排列组合公式为复杂度分析 - 图5 ，结果就是 n!，也就是说使用程序遍历所有情况，那么它的时间复杂度也就是 O(n!)。

代码实现如下，同样是通过回溯算法思想实现，当然，我们假设 int[] arr 不为空。也不需要刻意理解这段代码，在回溯算法思想中我将会给出详细介绍。

void arrayPermutations(int[] arr, int i, Queue<Integer> queue, int[] result) {
  if (i == arr.length) {
    System.out.println(Arrays.toString(result));
  }
  int size = queue.size();
  for (int j = 0; j < size; j++) {
    Integer index = queue.poll();
    result[i] = arr[index];
    arrayPermutations(arr, i+1, queue, result);
    queue.add(index);
  }
}

// 运行
int[] arr = new int[]{1,2,3,4,5};
for (int i : arr) {
  queue.add(i);
}
arrayPermutations(arr, 0, queue, new int[arr.length]);

2.4. 常见时间复杂度曲线图

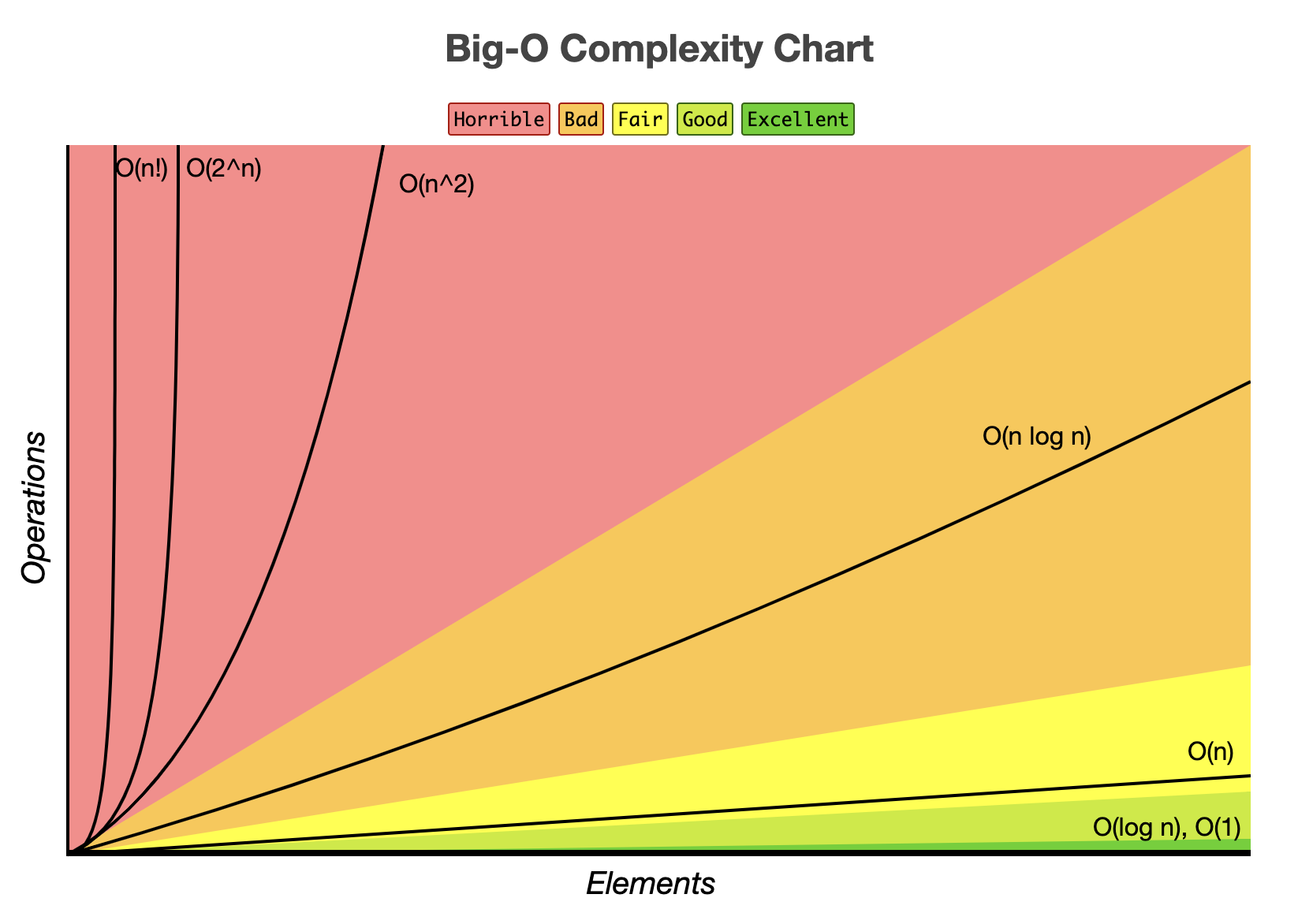
图片来源 https://www.bigocheatsheet.com/

3. 空间复杂度

只要清楚申请的额外空间作用即可准确计算，需要注意递归因为使用到计算机调用栈，所以其空间计算也不能忽视。
现在来看一个例子，将数组中的小写字母记录到一个新数组中，注意仅限小写字母。

byte[] containsLowerCases = ...;
byte[] result = new byte[containsLowerCases.length];
int j = 0;
for (int i = 0; i < containsLowerCases.length; i++) {
  if (isLowerCase(containsLowerCases[i]) {
    result[j++] = containsLowerCases[i];
  }
}

boolean isLowerCase(int ch) {
  return 97 <= ch && ch <= 122;
}

也许你已经发现，containsLowerCases 并不会全部都是小写，甚至可能不存在小写字母，但我们依然申请了一个长度与 containsLowerCases 相同的的结果数组，而且 containsLowerCases 有可能全部都是小写字母，所以我们应该以最大的空间来计算，即 O(n)。