冒泡排序
    冒泡排序需要两个嵌套的循环. 其中, 外层循环移动游标; 内层循环遍历游标及之后(或之前)的元素, 通过两两交换的方式, 每次只确保该内循环结束位置排序正确, 然后内层循环周期结束, 交由外层循环往后(或前)移动游标, 随即开始下一轮内层循环, 以此类推, 直至循环结束.
    Tips: 由于冒泡排序只在相邻元素大小不符合要求时才调换他们的位置, 它并不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.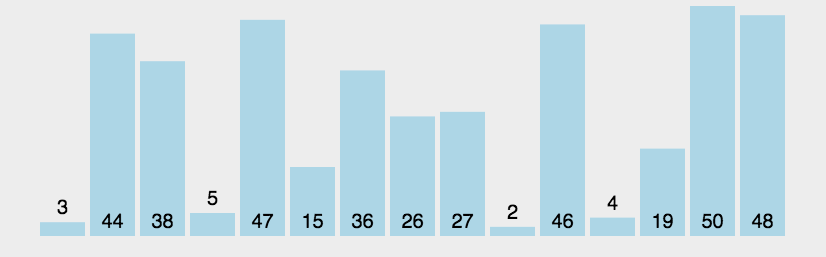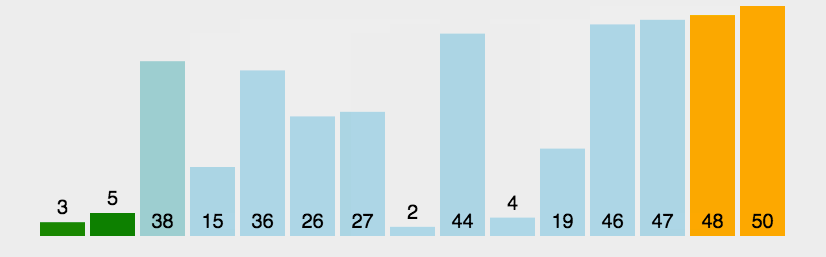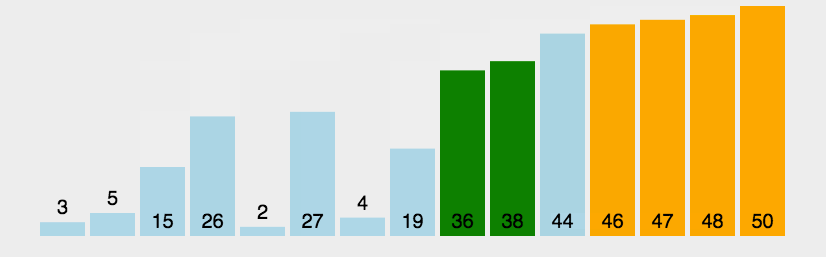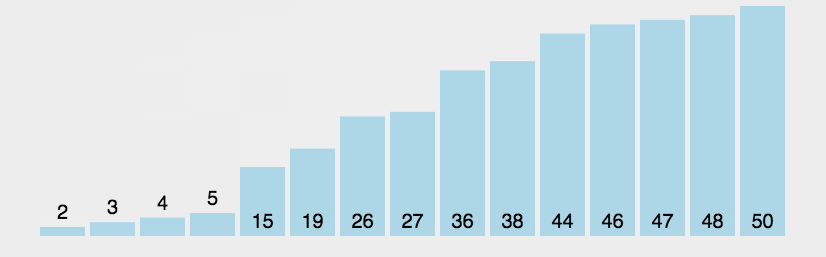
    经典的算法排序 - 图1

    1. function bubbleSort(arr){
    2.     for(let i=0;i<arr.length;i++){
    3.     for(let j=0;j<arr.length-1;j++){
    4.       if(arr[j]>arr[j+1]){
    5.         [arr[j],arr[j+1]] = [arr[j+1],arr[j]]
    6.       }
    7.     }
    8.   }
    9.   return arr
    10. }
    11. let a = bubbleSort([23, 334, 54, 3445, 5645, 24, 5634, 5656, 23, 65, 43, 554])
    12. console.log(a);//[23, 23, 24, 43, 54, 65, 334, 554, 3445, 5634, 5645, 5656]

    双向冒泡排序
    传统冒泡排序中每一趟排序操作只能找到一个最大值或最小值,我们考虑利用在每趟排序中进行正向和反向两遍冒泡的方法一次可以得到两个最终值(最大者和最小者) , 从而使排序趟数几乎减少了一半。

    1. function bothwayBubbleSort(arr){
    2.     let low = 0;
    3.   let high = arr.length-1; //设置变量的初始值
    4.   while(low<high){
    5.       for(let j=low;j<high;++j){ //正向冒泡,找到最大者
    6.       if (arr[j]> arr[j+1]){
    7.         [arr[j],arr[j+1]] = [arr[j+1],arr[j]]
    8.       }
    9.     }
    10.     --high //修改high值, 前移一位
    11.     for(let j=high;j>low;--j){ //反向冒泡,找到最小者
    12.       if (arr[j]<arr[j-1]){
    13.         [arr[j],arr[j-1]] = [arr[j-1],arr[j]]
    14.       }
    15.     }
    16.     ++low //修改low值,后移一位
    17.   }
    18.   return arr
    19. }
    21. var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
    22. console.log(bothwayBubbleSort(arr))//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

    选择排序
    原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。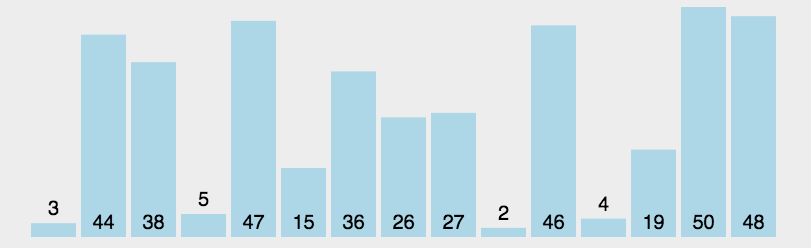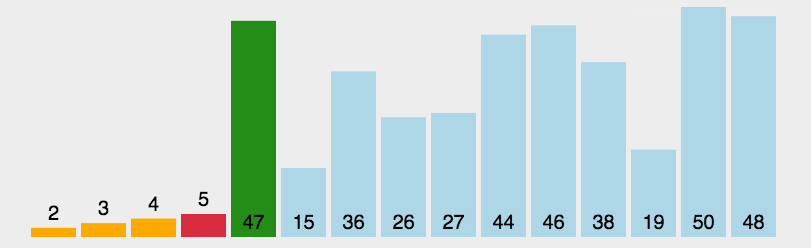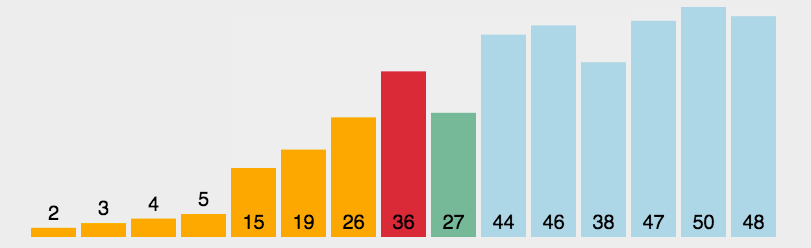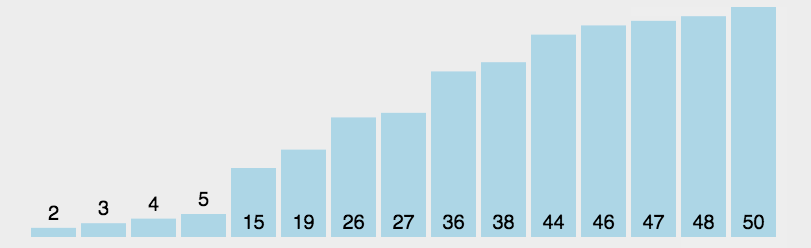
    经典的算法排序 - 图2

    1. /**
    2.  * 选择排序
    3.  * 每次都找到最小的然后放在第一个
    4.  * 时间复杂度O(n2)
    5.  */
    7. function selectSort(arr){
    8.   for(let i=0;i<arr.length-1;i++){
    9.     for(let j =i+1;j<arr.length;j++){
    10.       if(arr[i]>arr[j]){ //每次都与arr[i]作对比，筛选出最小值赋值到arr[i]
    11.         [arr[i],arr[j]] = [arr[j],arr[i]]
    12.       }
    13.     }
    14.   }
    15.   return arr
    16. }
    18. var arr = [23,334,54,3445,5645,24,5634,5656,23,65,43,554]
    19. console.log(selectSort(arr))//[23, 23, 24, 43, 54, 65, 334, 554, 3445, 5634, 5645, 5656]

    插入排序
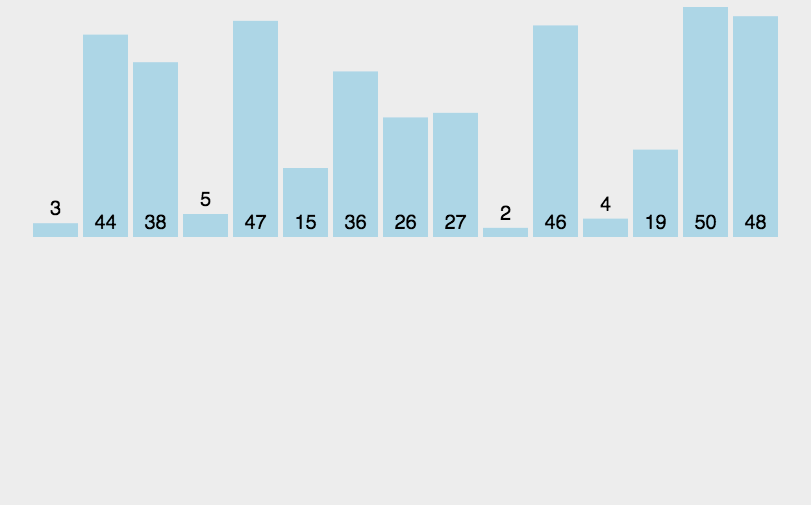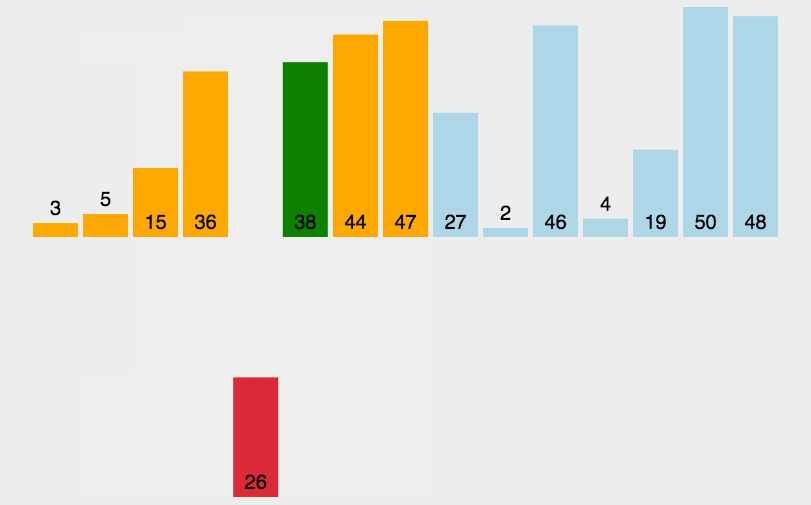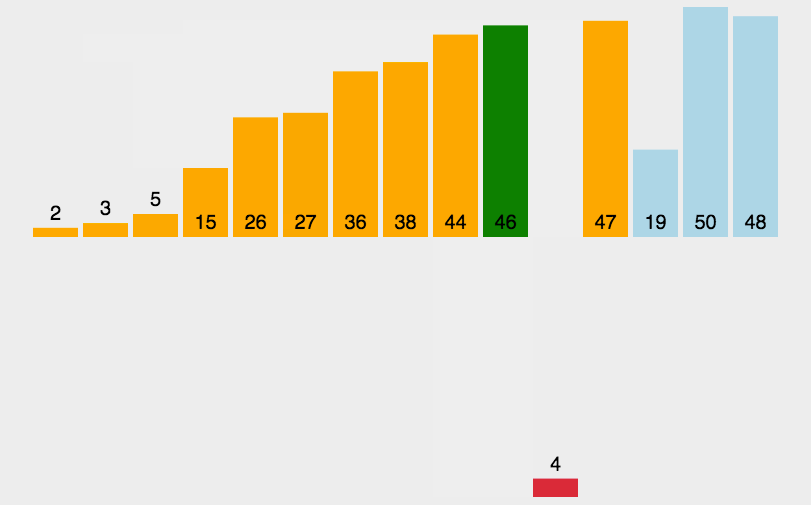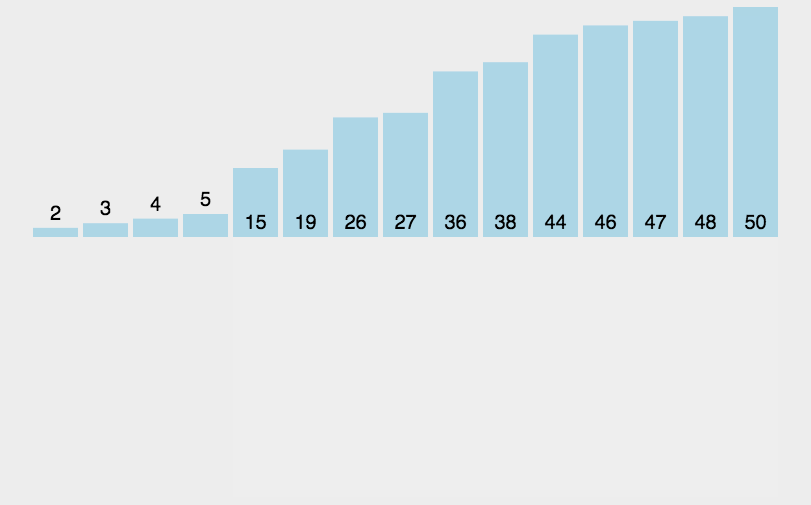
    一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

    • <1>.从第一个元素开始，该元素可以认为已经被排序；
    • <2>.取出下一个元素，在已经排序的元素序列中从后向前扫描；
    • <3>.如果该元素（已排序）大于新元素，将该元素移到下一位置；
    • <4>.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
    • <5>.将新元素插入到该位置后；
    • <6>.重复步骤2~5。

    经典的算法排序 - 图3

    1. function insertSort(arr){
    2.   for(let i = 1;i<arr.length;i++){
    3.     let count = i;
    4.     while(count>0){ //新元素与已排列好的数据逐个比对，插入到合适位置
    5.       if(arr[count]<arr[count-1]){
    6.         [arr[count],arr[count-1]]=[arr[count-1],arr[count]]
    7.       }
    8.       count-- 
    9.     }
    10.   }
    11.   return arr
    12. }
    14. var arr = [23,334,54,3445,5645,24,5634,5656,23,65,43,554]
    15. console.log(insertSort(arr))

    归并排序
    归并排序建立在归并操作之上, 它采取分而治之的思想, 将数组拆分为两个子数组, 分别排序, 最后才将两个子数组合并; 拆分的两个子数组, 再继续递归拆分为更小的子数组, 进而分别排序, 直到数组长度为1, 直接返回该数组为止.
    Tips: 归并排序严格按照从左往右(或从右往左)的顺序去合并子数组, 它并不会改变相同元素之间的相对顺序, 因此它也是一种稳定的排序算法.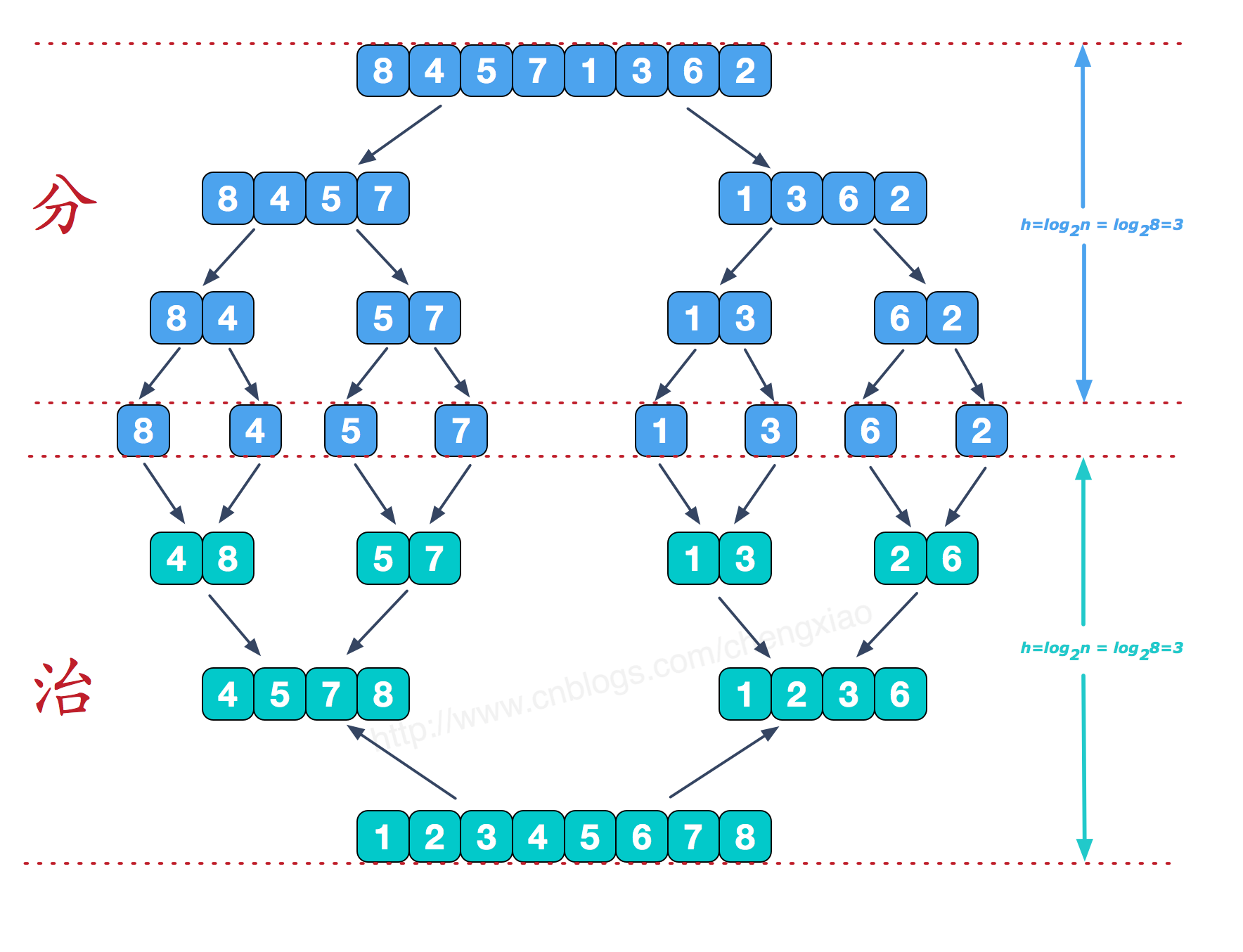
    经典的算法排序 - 图4
    经典的算法排序 - 图5

    1. function mergeSort(arr) {
    2.   if(arr.length<2){
    3.     return arr
    4.   }
    5.   const middleLength = Math.floor((arr.length/2)) //分成两个数组
    6.   const left = arr.slice(0,middleLength)
    7.   const right = arr.slice(middleLength,arr.length)
    8.   return merge(mergeSort(left),mergeSort(right)) //递归切分直到每个数组只剩下一个元素为止
    9. }
    11. function merge(left,right){ //按排序合并两个子数组
    12.   const result = []
    13.    while (left.length && right.length) { 
    14.         if (left[0] <= right[0]) {
    15.             result.push(left.shift());
    16.         } else {
    17.             result.push(right.shift());
    18.         }
    19.     } 
    20.   //若出现单数情况，最后剩下的值push进数组
    21.     while (left.length)
    22.         result.push(left.shift());
    23.     while (right.length)
    24.         result.push(right.shift());
    25.     return result;
    26. }
    27. console.log(mergeSort([23,334,54,3445,5645,24,5634,5656,23,65,43,554]))

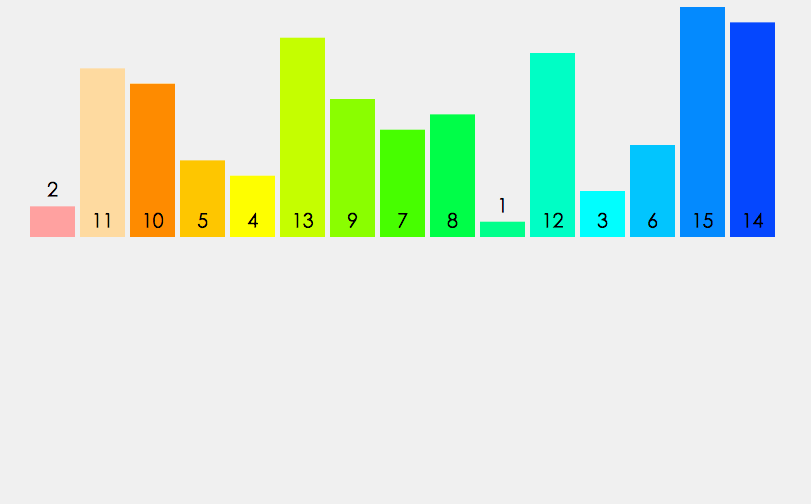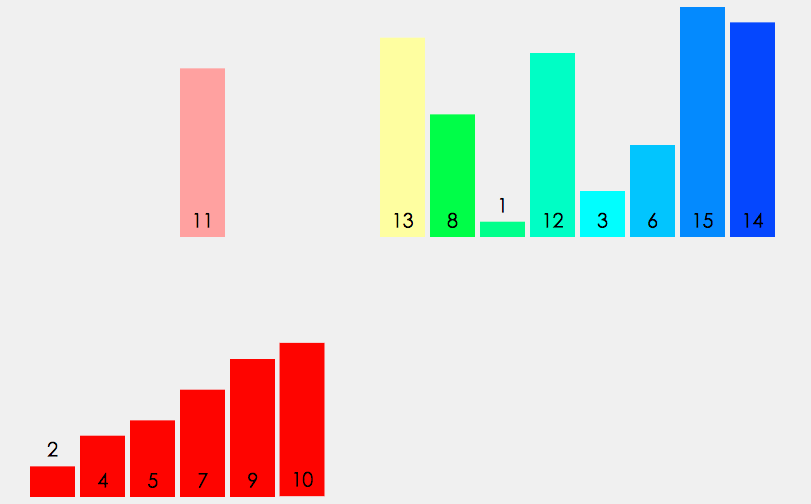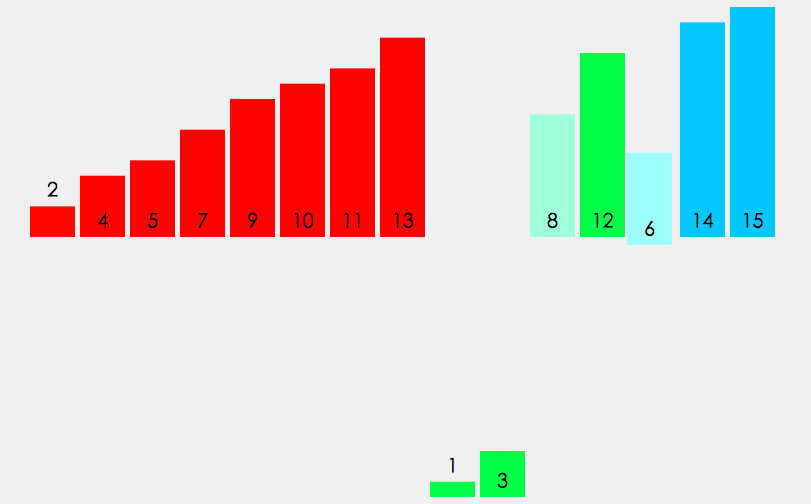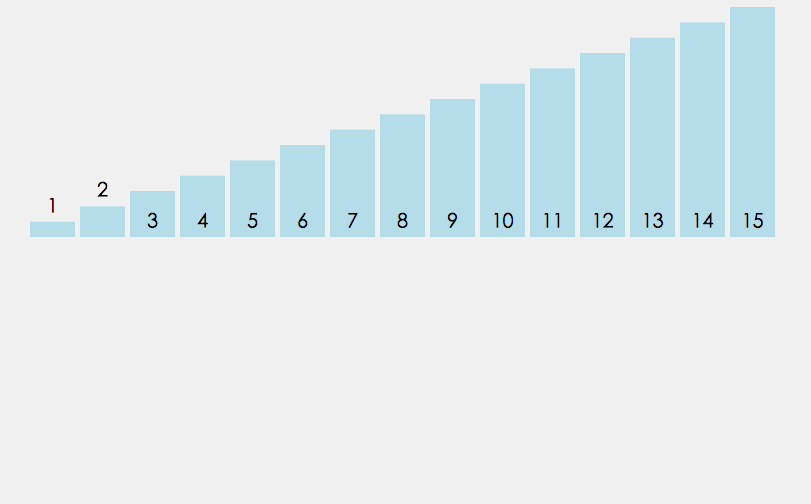
    快速排序
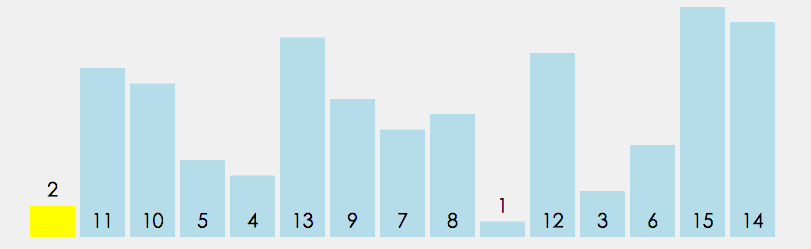
    快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

    • <1>.从数列中挑出一个元素，称为 “基准”（pivot）；
    • <2>.重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
    • <3>.递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

    535286772045a9c9c5031268e5e9250f.gif

    1. function swap(items, leftIndex, rightIndex) { //交换值函数
    2.   var temp = items[rightIndex]
    3.   items[rightIndex] = items[leftIndex]
    4.   items[leftIndex] = temp
    5. }
    8. function partition(items, left, right) {
    9.   var pivot = items[Math.floor((left + right) / 2)] //取位于数组长度的一半的数为基准数
    10.   var i = left
    11.   var j= right
    12.   while (i <= j) { //从两端分别与基准数比较
    13.     while (items[i] < pivot) { //从左开始，比基准数小时，i++
    14.       i++
    15.     }
    16.     while (items[j] > pivot) { //从右开始，比基准数大时，j--
    17.       j--
    18.     }
    19.     if (i <= j) { 
    20.       swap(items, i, j) //交换筛选出的两个值到合适的位置（左边<基准数<右边）
    21.       i++ //交换值后，继续比较数组剩余位置的值
    22.       j--
    23.     }
    24.   }
    25.   return i  //比较进行至i>j后结束并得出中位数的index值
    26. }
    28. function quickSort(items,left,right) {
    29.   if(items.length>1){
    30.     var index = partition(items,left,right)  //求出数组中位数的index
    31.     if(left<index-1){ //以中位数分割成两个数组，递归继续比较各自的数组中位数
    32.       quickSort(items,left,index-1)
    33.     }
    34.     if(right>index){
    35.       quickSort(items,index,right)
    36.     }
    37.   }
    38.   return items
    39. }
    40. let arr = [23,334,54,3445,5645,24,5634,5656,23,65,43,554]
    41. console.log(quickSort(arr,0,arr.length-1))

    计数排序

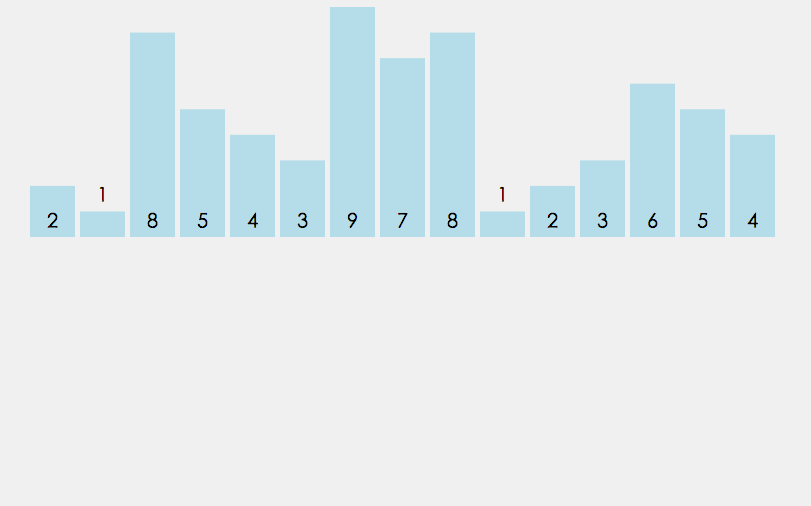
    1. 获取待排序数组A的最大值, 最小值.
    2. 将最大值与最小值的差值+1作为长度新建计数数组B，并将相同元素的数量作为值存入计数数组.
    3. 对计数数组B累加计数, 存储不同值的初始下标.
    4. 从原数组A挨个取值, 赋值给一个新的数组C相应的下标, 最终返回数组C.

    2f474809cbbae9e2ae73e761e446b400.gif

    1. /**
    2.  * 计数排序
    3.  * 新建一个数组，统计每个数字出现的次数
    4.  * 假设我们有[1,2,3,1,0,4]这六个数，这里面最大的值为4，
    5.  * 那么我们创建一个长度为4的数组，每个元素默认为0。
    6.  * 这相当于选举排序，一共有6个投票箱，1就投1号箱，0就投入0号箱。
    7.  * 这些箱的所有数依次出来，放到新数组，就神奇地排好序了
    8.  * 负数处理
    9.  */
    11. function countSort(arr){
    12.   var max = arr[0]
    13.   var min = arr[0]
    14.   var result = []
    15.   for(var i = 0; i < arr.length; i++){ //获取待排序数组A的最大值, 最小值.
    16.     if(arr[i] > max){
    17.         max = arr[i] 
    18.     }
    19.     if(arr[i] < min){
    20.         min = arr[i]
    21.     }
    22.   }
    24.   //将最大值与最小值的差值+1作为长度新建计数数组countArr，每项初始值0
    25.   var countArr = new Array(max-min+1).fill(0) 
    26.     //对计数数组countArr累加计数, 存储不同值的初始下标.
    27.   for(var i = 0; i <arr.length; i++){
    28.     countArr[arr[i]-min]++
    29.   }
    30.   //从原数组countArr挨个取值, 赋值给一个新的数组result相应的下标, 最终返回数组result
    31.   for(var i = 0; i <countArr.length;i++){
    32.     while(countArr[i]>0){
    33.       result.push(i+min)
    34.       countArr[i]--
    35.     }
    36.   }
    37.   return result
    38. }
    40. let a =countSort([2,2,4,3,6,7,4,8,2,16])
    41. console.log(a);//[2, 2, 2, 3, 4, 4, 6, 7, 8, 16]