Struct

  1. type Tree struct {
  2.     Root       *Node            
  3.     Comparator utils.Comparator 
  4.     size       int              
  5. }
  7. type Node struct {
  8.     Key      interface{}
  9.     Value    interface{}
  10.     Parent   *Node    
  11.     Children [2]*Node 
  12.     b        int8
  13. }

这里子树，并没有用左右来表示，而是直接使用了一个数组，数组的 0 号元素相当于左树，1 号相当于右树，这和一会需要做的旋转操作也有关系。
存储的结构是 Key - Value 形式的，key 也作为树的关键字，它的比较函数存储在 Comparator 字段中，因为树的插入，删除，查找等工作都需要进行对比，使用规律非常频繁。
b 就是使这个二叉树保持平衡的关键了，按照常理来说它应该是指 avl 树的高度吧，但是高度不应该直接用 h 表示吗，为什么用了 b 这个字母，这一点还需要在代码中考察。

Floor() & Ceiling()

这里有两个比较特别的函数， Floor() 是用来寻找小于或等于给定节点的最大节点， Ceiling() 则是寻找大于或等于给定节点的最小函数。

  1. func (t *Tree) Floor(key interface{}) (floor *Node, found bool) 
  2. func (t *Tree) Ceiling(key interface{}) (floor *Node, found bool)

最后的布尔值表示是否查找成功，不成功有两种情况，树为空，所有节点都比给定节点大（小）。

Put()

为了保证 AVL 树的左子树和右子树的最大高度差为 1，我们肯定需要监控树的高度，那么树的高度发生变化只有在插入或者删除的时候。我们先来看一下插入的函数

  1. func (t *Tree) Put(key interface{}, value interface{}) {
  2.     t.put(key, value, nil, &t.Root)
  3. }
  4. func (t *Tree) put(key interface{}, value interface{}, p *Node, qp **Node)

很轻松的就可以看出，这里真正的实现函数是 put() 函数，下面是它的函数签名，那后面的 qp 是什么意思，为什么它是二重指针，p 在这里又代表了什么
这里 qp 应该是指 q 的 pointer，因为节点是使用 *Node 存放的，所以 q 的指针就应该使用二重指针了，那这里为什么必须要传指针呢，这里 p 是代表的 parent，如果我们传递的是 p 的 children 那么修改的时候并不会对 p 中的 children 产生影响，所以这里必须传递二重指针。

  1. func (t *Tree) put(key interface{}, value interface{}, p *Node, qp **Node) bool {
  2.     q := *qp
  3.     if q == nil {
  4.         t.size++
  5.         *qp = &Node{Key: key, Value: value, Parent: p}
  6.         return true
  7.     }
  9.     c := t.Comparator(key, q.Key)
  10.     if c == 0 {
  11.         q.Key = key
  12.         q.Value = value
  13.         return false
  14.     }
  16.     if c < 0 {
  17.         c = -1
  18.     } else {
  19.         c = 1
  20.     }
  21.     a := (c + 1) / 2
  22.     var fix bool
  23.     fix = t.put(key, value, q, &q.Children[a])
  24.     if fix {
  25.         return putFix(int8(c), qp)
  26.     }
  27.     return false
  28. }

在这段代码中我们可以看到， put() 是递归调用的，而决定是否需要修改节点的是由 fix 这个变量决定的，这里有这里给出了两种可能一种是新建节点必须检查，另一个是由 putFix() 决定的，我们再观察 putFix() 这个函数的签名， func putFix(c int8, t **Node) ，发现它不但传递了新建的节点，而且还将比较的结果也传进去了， c == 1 时，新建的节点是右子树， c == -1 时，新建节点在左子树，这就将左旋和右旋分割开来，只需要调用一个函数就可以了，大大降低了思考的成本。

  1. func putFix(c int8, t **Node) bool {
  2.     s := *t
  3.     if s.b == 0 {
  4.         s.b = c
  5.         return true
  6.     }
  8.     if s.b == -c {
  9.         s.b = 0
  10.         return false
  11.     }
  13.     if s.Children[(c+1)/2].b == c {
  14.         s = singlerot(c, s)
  15.     } else {
  16.         s = doublerot(c, s)
  17.     }
  18.     *t = s
  19.     return false
  20. }

首先我们按照第一次插入来看这个函数，最末端一次调用的时候，qp 是 k3，是新建的节点，那么当这个函数返回，调用 futFix() 的时候 pq 就应该是 k2 了，其实这里的 b 是记录上次插入的位置，如果我们上次对这个节点在左子树上进行插入，那么我们下次如果还在左子树上插入就不平衡了，所以 b 是为了限制不能在同一个方向上连续插入两次。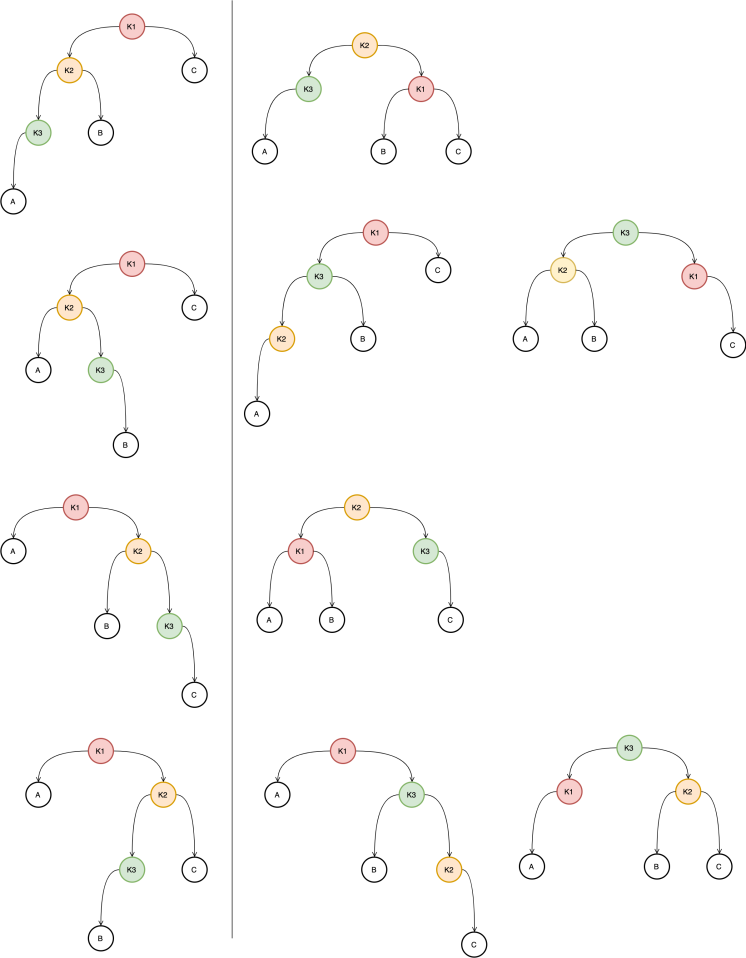
1571644417619-c419cc50-d9e2-4e3b-b7f4-b8cb8e4fd5b7.png

  1. func singlerot(c int8, s *Node) *Node {
  2.     s.b = 0
  3.     s = rotate(c, s)
  4.     s.b = 0
  5.     return s
  6. }
  8. func doublerot(c int8, s *Node) *Node {
  9.     a := (c + 1) / 2
  10.     r := s.Children[a]
  11.     s.Children[a] = rotate(-c, s.Children[a])
  12.     p := rotate(c, s)
  14.     switch {
  15.     default:
  16.         s.b = 0
  17.         r.b = 0
  18.     case p.b == c:
  19.         s.b = -c
  20.         r.b = 0
  21.     case p.b == -c:
  22.         s.b = 0
  23.         r.b = c
  24.     }
  26.     p.b = 0
  27.     return p
  28. }
  30. func rotate(c int8, s *Node) *Node {
  31.     a := (c + 1) / 2
  32.     r := s.Children[a]
  33.     s.Children[a] = r.Children[a^1]
  34.     if s.Children[a] != nil {
  35.         s.Children[a].Parent = s
  36.     }
  37.     r.Children[a^1] = s
  38.     r.Parent = s.Parent
  39.     s.Parent = r
  40.     return r
  41. }

Remove()

同样 Remove() 的底层是 remove() ，而且也是使用递归进行删除，参数的传递也是二重指针，这样才能保证影响到存储这个节点的每个位置。
我们先来看一下真正的删除代码，如果当前的 Key 和需要删除的 Key 相同，就需要对这个节点进行删除，并且找一个节点来这里填充这个节点，这个实现中选择的是右子树的最小节点，当然也可以是左子树的最大节点。

  1.     c := t.Comparator(key, q.Key)    
  2.     if c == 0 {
  3.         t.size--
  4.         if q.Children[1] == nil {
  5.             if q.Children[0] != nil {
  6.                 q.Children[0].Parent = q.Parent
  7.             }
  8.             *qp = q.Children[0]
  9.             return true
  10.         }
  11.         fix := removeMin(&q.Children[1], &q.Key, &q.Value)
  12.         if fix {
  13.             return removeFix(-1, qp)
  14.         }
  15.         return false
  16.     }
  18. func removeMin(qp **Node, minKey *interface{}, minVal *interface{}) bool {
  19.     q := *qp
  20.     if q.Children[0] == nil {
  21.         *minKey = q.Key
  22.         *minVal = q.Value
  23.         if q.Children[1] != nil {
  24.             q.Children[1].Parent = q.Parent
  25.         }
  26.         *qp = q.Children[1]
  27.         return true
  28.     }
  29.     fix := removeMin(&q.Children[0], minKey, minVal)
  30.     if fix {
  31.         return removeFix(1, qp)
  32.     }
  33.     return false
  34. }