struct

与 AvlTree 唯一的不同就是少了一个 b 多了一个 color，这个 color 的定义也非常简单就是红和黑，都是用 bool 值来存储。重要的是它如何实现红黑树的几个特性。

  1. type Tree struct {
  2.     Root       *Node
  3.     size       int
  4.     Comparator utils.Comparator
  5. }
  7. type Node struct {
  8.     Key    interface{}
  9.     Value  interface{}
  10.     color  color
  11.     Left   *Node
  12.     Right  *Node
  13.     Parent *Node
  14. }
  16. type color bool
  18. const (
  19.     black, red color = true, false
  20. )

Put()

我们直接来看 Put() ，签名与普通的函数没有区别，里面也是使用循环而不是递归，插入过程也很基本，比较现在这个节点和需要插入的 Key 的大小，大的话向右走，小的话向左走。直到最后插入。但是在最后需要检验是否满足红黑树的性质，细心的人应该能注意到无论怎么插入这里新插入的节点颜色都是红色。

  1. func (tree *Tree) Put(key interface{}, value interface{}) {
  2.     var insertedNode *Node
  3.     if tree.Root == nil {
  4.         // Assert key is of comparator's type for initial tree
  5.         tree.Comparator(key, key)
  6.         tree.Root = &Node{Key: key, Value: value, color: red}
  7.         insertedNode = tree.Root
  8.     } else {
  9.         node := tree.Root
  10.         loop := true
  11.         for loop {
  12.             compare := tree.Comparator(key, node.Key)
  13.             switch {
  14.             case compare == 0:
  15.                 node.Key = key
  16.                 node.Value = value
  17.                 return
  18.             case compare < 0:
  19.                 if node.Left == nil {
  20.                     node.Left = &Node{Key: key, Value: value, color: red}
  21.                     insertedNode = node.Left
  22.                     loop = false
  23.                 } else {
  24.                     node = node.Left
  25.                 }
  26.             case compare > 0:
  27.                 if node.Right == nil {
  28.                     node.Right = &Node{Key: key, Value: value, color: red}
  29.                     insertedNode = node.Right
  30.                     loop = false
  31.                 } else {
  32.                     node = node.Right
  33.                 }
  34.             }
  35.         }
  36.         insertedNode.Parent = node
  37.     }
  38.     tree.insertCase1(insertedNode)
  39.     tree.size++
  40. }

case1

第一种情况，父节点为 nil，那么新插入的就是根结点，根节点必须为黑，其实这中检验完全可以没有，直接插入根结点的话为黑就可以了，虽然提高不了多少性能，因为根结点的插入也就这一次而已。

  1. func (tree *Tree) insertCase1(node *Node) {
  2.     if node.Parent == nil {
  3.         node.color = black
  4.     } else {
  5.         tree.insertCase2(node)
  6.     }
  7. }

case2

父节点颜色为黑，满足条件完成

  1. func (tree *Tree) insertCase2(node *Node) {
  2.     if nodeColor(node.Parent) == black {
  3.         return
  4.     }
  5.     tree.insertCase3(node)
  6. }

case3

父节点是红色，祖父节点肯定是黑色，需要将父节点调整为黑色，该路径上黑色增加了，将祖父节点换为红色，现在出现了新问题，另一个是祖父节点的另一个儿子，我们把它叫做兄弟节点，是不是红色，需不需要改变

  1. 兄弟节点是红色，需要将叔节点变为黑色，保证性质 5，祖父节点的父亲不知道是不是红色，所以我们递归的调用这个函数，检测祖父节点能否满足
  2. 兄弟节点是黑色，完蛋，没办法变颜色了，这个时候我们需要通过其他方法来解决问题
    1. func (tree *Tree) insertCase3(node *Node) {
    2. uncle := node.uncle()
    3. if nodeColor(uncle) == red {
    4.   node.Parent.color = black
    5.   uncle.color = black
    6.   node.grandparent().color = red
    7.   tree.insertCase1(node.grandparent())
    8. } else {
    9.   tree.insertCase4(node)
    10. }
    11. }

    case4

    解决的情况就是父节点是红色，兄弟节点也是红色，这里有四种情况，分别是新增节点是左子树的左儿子，是左子树的右儿子，是右子树的左儿子还有是右子树的右儿子，就是把左右重新组合了而已。

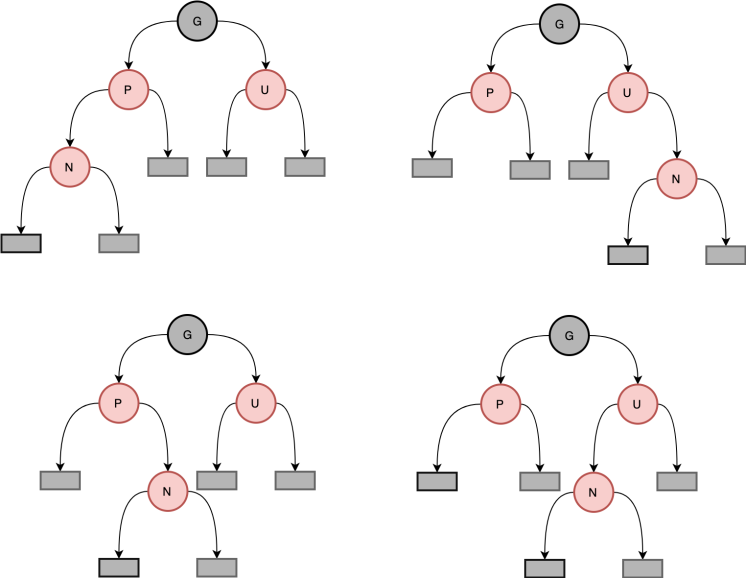
1571909841429-822c7df5-4eeb-41b1-8579-3c3fd738bd3f.png


前两种和后两种的区别只有左右不同，所以这里我们不再进行讨论。

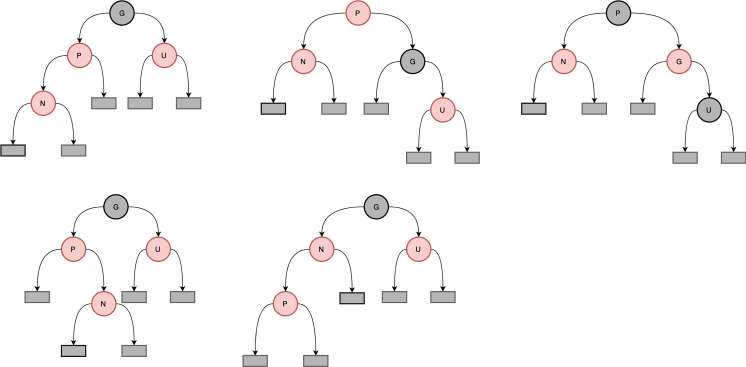
1571909861652-cac41ae3-3435-4163-bec8-d740d744fb75.png

  1. func (tree *Tree) insertCase4(node *Node) {
  2.     grandparent := node.grandparent()
  3.     if node == node.Parent.Right && node.Parent == grandparent.Left {
  4.         tree.rotateLeft(node.Parent)
  5.         node = node.Left
  6.     } else if node == node.Parent.Left && node.Parent == grandparent.Right {
  7.         tree.rotateRight(node.Parent)
  8.         node = node.Right
  9.     }
  10.     tree.insertCase5(node)
  11. }

case5

其实 case4 和 case 5 是很相似的，他们完全可以算作一个 case 只是两个步骤而已

  1. func (tree *Tree) insertCase5(node *Node) {
  2.     node.Parent.color = black
  3.     grandparent := node.grandparent()
  4.     grandparent.color = red
  5.     if node == node.Parent.Left && node.Parent == grandparent.Left {
  6.         tree.rotateRight(grandparent)
  7.     } else if node == node.Parent.Right && node.Parent == grandparent.Right {
  8.         tree.rotateLeft(grandparent)
  9.     }
  10. }

Remove()

对一个节点进行移除的第一步肯定是要先找到这个节点了，这一步被封装在 loolup() 中，其实和普通二叉树的操作方法是一样的。然后第二步如果两侧都不为空用左子树中最大的节点替换这个节点，和添加的选择正好相反。
我们将剩下的问题转换成了剩下两种情况.
现在的 node 两侧至少有一个为 nil，所以下面这个 if 语句一定是成立的，那就能把它删去了呀。

  1. func (tree *Tree) Remove(key interface{}) {
  2.     var child *Node
  3.     node := tree.lookup(key)
  4.     if node == nil {
  5.         return
  6.     }
  7.     if node.Left != nil && node.Right != nil {
  8.         pred := node.Left.maximumNode()
  9.         node.Key = pred.Key
  10.         node.Value = pred.Value
  11.         node = pred
  12.     }
  13.     if node.Left == nil || node.Right == nil {
  14.         if node.Right == nil {
  15.             child = node.Left
  16.         } else {
  17.             child = node.Right
  18.         }
  19.         if node.color == black {
  20.             node.color = nodeColor(child)
  21.             tree.deleteCase1(node)
  22.         }
  23.         tree.replaceNode(node, child)
  24.         if node.Parent == nil && child != nil {
  25.             child.color = black
  26.         }
  27.     }
  28.     tree.size--
  29. }

现在如果这个节点是红色，那么直接用子节点替换就可以，无论子节点是空的或者是黑色，如果是黑色，直接删除会导致黑色节点数量改变，也可能子节点和父节点都是红色，那我们就需要检验

case1

最开始看到这种情况，可能会想最后发生替换的时候也需要检查是不是根结点，case1 是不是没有必要啊？其实并不是，如果没有父节点，那我们下面的操作就没法去做，所以一定需要事先检查，否则进入下面情况可能会报错

  1. func (tree *Tree) deleteCase1(node *Node) {
  2.     if node.Parent == nil {
  3.         return
  4.     }
  5.     tree.deleteCase2(node)
  6. }

case2

兄弟节点是红色，兄弟的儿子都是黑色，父亲是黑色，左旋，满足条件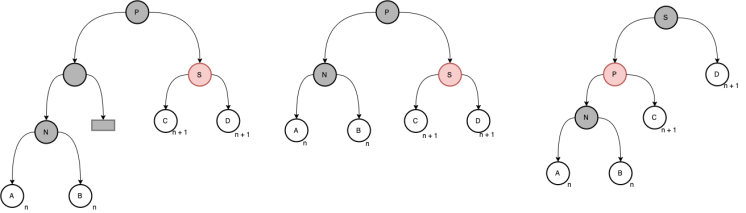
1571928668985-9fd37c02-b791-49de-86c8-88e2c4af0c67.png

  1. func (tree *Tree) deleteCase2(node *Node) {
  2.     sibling := node.sibling()
  3.     if nodeColor(sibling) == red {
  4.         node.Parent.color = red
  5.         sibling.color = black
  6.         if node == node.Parent.Left {
  7.             tree.rotateLeft(node.Parent)
  8.         } else {
  9.             tree.rotateRight(node.Parent)
  10.         }
  11.     }
  12.     tree.deleteCase3(node)
  13. }

case3

兄弟节点是黑色，儿子都是黑色，父亲是黑色，将兄弟节点变为红色，所有通过父亲的路径都减少一，对父亲重复调整颜色的过程

  1. func (tree *Tree) deleteCase3(node *Node) {
  2.     sibling := node.sibling()
  3.     if nodeColor(node.Parent) == black &&
  4.         nodeColor(sibling) == black &&
  5.         nodeColor(sibling.Left) == black &&
  6.         nodeColor(sibling.Right) == black {
  7.         sibling.color = red
  8.         tree.deleteCase1(node.Parent)
  9.     } else {
  10.         tree.deleteCase4(node)
  11.     }
  12. }

case4

兄弟节点是黑色，父亲是红色，交换父亲和兄弟的颜色，满足条件

  1. func (tree *Tree) deleteCase4(node *Node) {
  2.     sibling := node.sibling()
  3.     if nodeColor(node.Parent) == red &&
  4.         nodeColor(sibling) == black &&
  5.         nodeColor(sibling.Left) == black &&
  6.         nodeColor(sibling.Right) == black {
  7.         sibling.color = red
  8.         node.Parent.color = black
  9.     } else {
  10.         tree.deleteCase5(node)
  11.     }
  12. }

case5

兄弟节点是黑色，一个儿子是黑色，另一个是红色

  1. 左红右黑
  2. 右红左黑

两者只是方向相反而已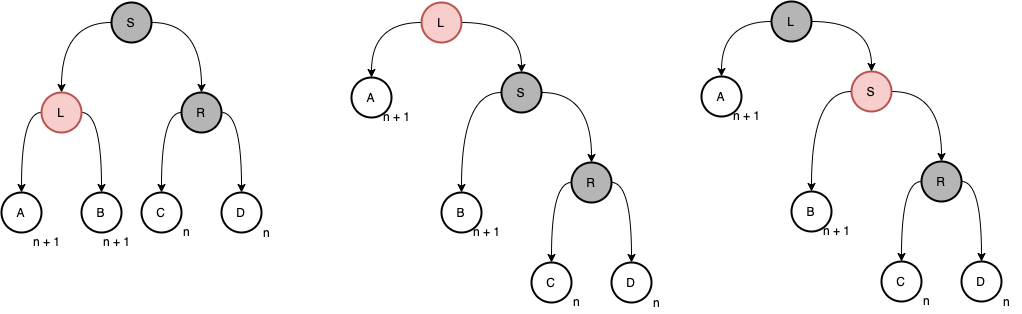Untitled Diagram (3).png通过这张图我们可以发现，父节点无论是红还是黑，对于操作是没有影响的，所以我们把它统一为一种情况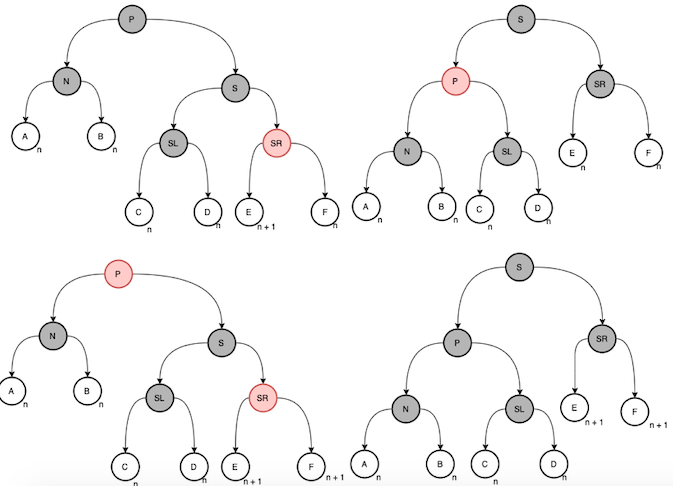Screen Shot 2019-10-25 at 11.14.41 AM.png

  1. func (tree *Tree) deleteCase5(node *Node) {
  2.     sibling := node.sibling()
  3.     if node == node.Parent.Left &&
  4.         nodeColor(sibling) == black &&
  5.         nodeColor(sibling.Left) == red &&
  6.         nodeColor(sibling.Right) == black {
  7.         sibling.color = red
  8.         sibling.Left.color = black
  9.         tree.rotateRight(sibling)
  10.     } else if node == node.Parent.Right &&
  11.         nodeColor(sibling) == black &&
  12.         nodeColor(sibling.Right) == red &&
  13.         nodeColor(sibling.Left) == black {
  14.         sibling.color = red
  15.         sibling.Right.color = black
  16.         tree.rotateLeft(sibling)
  17.     }
  18.     tree.deleteCase6(node)
  19. }

case6

两个都是红色同样是观察上图，最后的 P 都变为黑色，也就是说 SL 的颜色也不重要，所以上图可以简化为

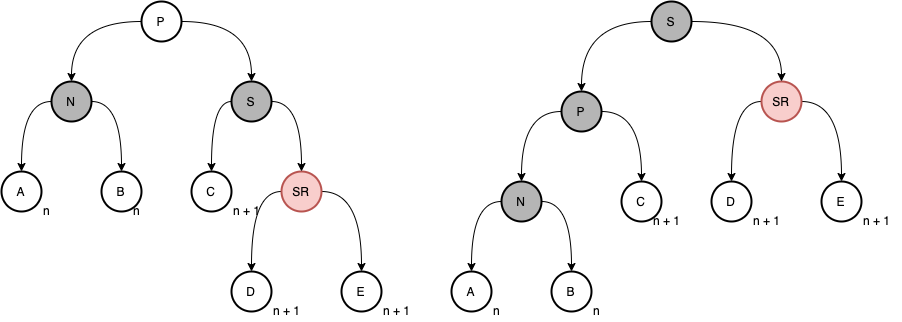
Untitled Diagram (2).png

  1. func (tree *Tree) deleteCase6(node *Node) {
  2.     sibling := node.sibling()
  3.     sibling.color = nodeColor(node.Parent)
  4.     node.Parent.color = black
  5.     if node == node.Parent.Left && nodeColor(sibling.Right) == red {
  6.         sibling.Right.color = black
  7.         tree.rotateLeft(node.Parent)
  8.     } else if nodeColor(sibling.Left) == red {
  9.         sibling.Left.color = black
  10.         tree.rotateRight(node.Parent)
  11.     }
  12. }