AVL

• 左旋和右旋示意图
• 四种情况及解决方案
• AVL 的逻辑分析
• AVL in Go

旋转

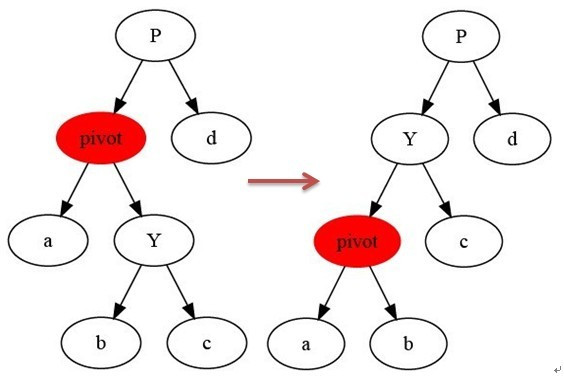
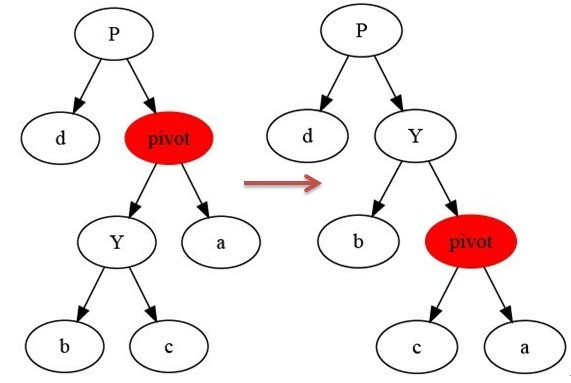
左旋

右旋

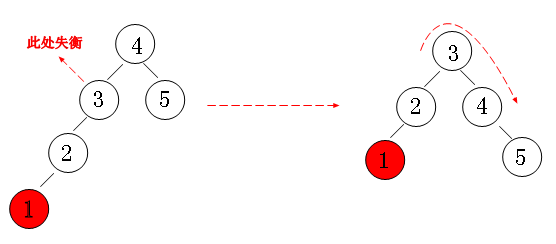
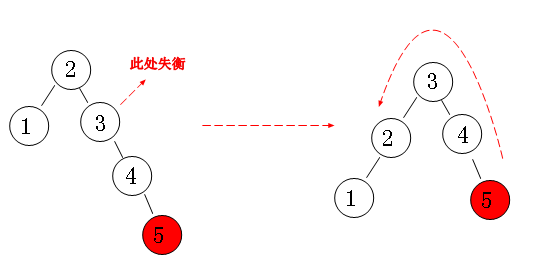
四种情况

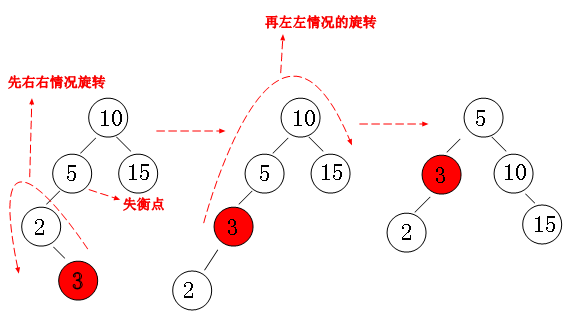
左左

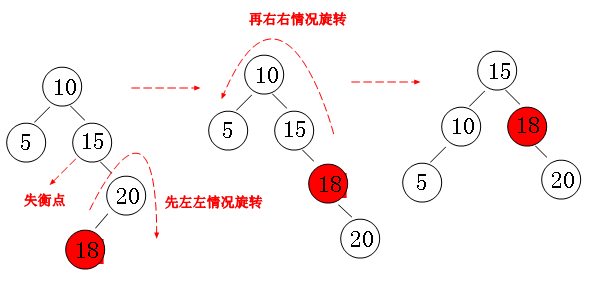
右右

左右

右左

逻辑分析

记录当前节点的状态 Abs(state) <= 1 ，每次发生一点不平衡就会修正，分为以上四种情况。

AVL in Golang

这段代码来自：gods

// Tree holds elements of the AVL tree.
type Tree struct {
    Root       *Node            // Root node
    Comparator utils.Comparator // Key comparator
    size       int              // Total number of keys in the tree
}
// Node is a single element within the tree
type Node struct {
    Key      interface{}
    Value    interface{}
    Parent   *Node    // Parent node
    Children [2]*Node // Children nodes
    b        int8
}

其中 b 是用来表明节点是否平衡的，children[0] 代表左节点，children[1] 代表右节点。后面通过亦或运算来统一左旋和右旋，很优秀。

func singlerot(c int8, s *Node) *Node {
    s.b = 0
    s = rotate(c, s)
    s.b = 0
    return s
}
func doublerot(c int8, s *Node) *Node {
    a := (c + 1) / 2
    r := s.Children[a]
    s.Children[a] = rotate(-c, s.Children[a])
    p := rotate(c, s)
    switch {
    default:
        s.b = 0
        r.b = 0
    case p.b == c:
        s.b = -c
        r.b = 0
    case p.b == -c:
        s.b = 0
        r.b = c
    }
    p.b = 0
    return p
}
// c < 0 时为右旋，c > 0 时为左旋
func rotate(c int8, s *Node) *Node {
    a := (c + 1) / 2
    r := s.Children[a]
    s.Children[a] = r.Children[a^1]
    if s.Children[a] != nil {
        s.Children[a].Parent = s
    }
    r.Children[a^1] = s
    r.Parent = s.Parent
    s.Parent = r
    return r
}

数学基础：

通过亦或，将左旋和右旋统一在一起，singlerot 统一了左左和右右的情况，doublerot 统一的左右和右左的情况。

整个流程通过参数 c 来控制左旋还是右旋，由 c 可以获取左节点还是有节点，节点位置 a = (c + 1) / 2

这里面只列出了部分关键代码，完整代码青岛 Github 上自行查看