B-Tree（Balanced Tree） - 《Computer Science》

定义
逻辑图
B-Tree in Go
- B-Tree 的定义
Put
Remove
Others

B-Tree 的定义
逻辑图
B-Tree in Go
定义

树的每个节点不超过 m 个儿子（其中 m 为二叉树的阶数）
除根节点和叶子节点之外的节点有不少于 [m / 2] 个儿子
根节点至少有两个儿子（除非它本身就是一个叶子节点）
所有的非根节点必须包含以下信息：
1. n 为关键字个数
2. 是关键字，从左到右升序排列
3. 是指向子节点的指针，指向一个关键字都在到之间的子树
所有的叶子节点都出现在同一层次上，并且不带任何信息（可以看做是外部节点，或者是查找失败节点，实际上，这些节点并不存在，指向这些节点的指针为空）

逻辑图

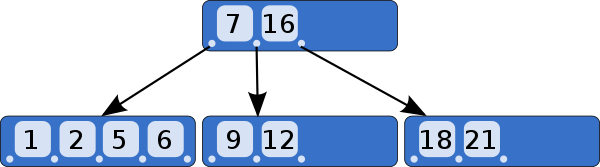
B-Tree in Go

代码来自：gods

B-Tree 的定义

// Get searches the node in the tree by key and returns its value or nil if key is not found in tree.
// Second return parameter is true if key was found, otherwise false.
// Key should adhere to the comparator's type assertion, otherwise method panics.
func (tree *Tree) Get(key interface{}) (value interface{}, found bool) {
    node, index, found := tree.searchRecursively(tree.Root, key)
    if found {
        return node.Entries[index].Value, true
    }
    return nil, false
}
// Tree holds elements of the B-tree
type Tree struct {
    Root       *Node            // Root node
    Comparator utils.Comparator // Key comparator
    size       int              // Total number of keys in the tree
    m          int              // order (maximum number of children)
}
// Node is a single element within the tree
type Node struct {
    Parent   *Node
    Entries  []*Entry // Contained keys in node
    Children []*Node  // Children nodes
}
// Entry represents the key-value pair contained within nodes
type Entry struct {
    Key   interface{}
    Value interface{}
}

// searchRecursively searches recursively down the tree starting at the startNode
func (tree *Tree) searchRecursively(startNode *Node, key interface{}) (node *Node, index int, found bool) {
    if tree.Empty() {
        return nil, -1, false
    }
    node = startNode
    for {
        index, found = tree.search(node, key)
        if found {
            return node, index, true
        }
        if tree.isLeaf(node) {
            return nil, -1, false
        }
        node = node.Children[index]
    }
}
// search searches only within the single node among its entries
func (tree *Tree) search(node *Node, key interface{}) (index int, found bool) {
    low, high := 0, len(node.Entries)-1
    var mid int
    for low <= high {
        mid = (high + low) / 2
        compare := tree.Comparator(key, node.Entries[mid].Key)
        switch {
        case compare > 0:
            low = mid + 1
        case compare < 0:
            high = mid - 1
        case compare == 0:
            return mid, true
        }
    }
    return low, false
}

二分查找

这里弄清楚 []*Entry 和 []*Node 下标之间的关系即可。

前面省略了 Get 和 searchRecursively 方法，如果 searchRecursively 在 search 外面包了一层 for 循环，用来查找节点。

这个函数在 Put 和 Remove 的实现中也用到了，因为可以查找到节点的位置。一般来说，暴露出去的函数只有那么简单的几个，而内部有很多复杂的非暴露出去的函数，这些函数分层次，分别处理完一部分工作，然后调用下一层的函数。这些抽象出来的函数一定会有重复利用的价值，不然任何意义。在 gods 的源码中，出现了循环调用的情况，即上层调用下层，下层也调用上层，虽然不算什么错，但是我不喜欢。那么我想换一种方式来实现这种功能。

Put

通常，键的数量被选定在 d 和 2d 之间。其中 d 是键的最小数量，是树最小的度或分支因子。在实际中，键值占用了节点中大部分的空间。因数 2 将保证节点可以被拆分或组合。如果一个内部节点有 2d 个键，那么要添加一个键值给此节点，只需要拆分这个键为 2 个拥有 d 个键的节点，并把中间值节点移动到父节点。每一个拆分的节点需要拥有足够数目的键。相似地，如果一个内部节点和他的邻居两者都有 d 个键，那么将通过它与邻居的合并来删除一个键。删除此键将导致此节点拥有 d-1 个键;与邻居的合并则加上 d 个键，再加上从邻居节点的父节点移来的一个键值。结果为完全填充的 2d 个键。

——维基百科

代码有点长，我们来一步一步分析

// 总体的 insert，里面调用了 tree 的两个方法，分别是 tree.insertIntoLeaf 和
// tree.insertIntoInternal
func (tree *Tree) insert(node *Node, entry *Entry) (inserted bool) {
    if tree.isLeaf(node) {
        return tree.insertIntoLeaf(node, entry)
    }
    return tree.insertIntoInternal(node, entry)
}
// 
func (tree *Tree) insertIntoLeaf(node *Node, entry *Entry) (inserted bool) {
    insertPosition, found := tree.search(node, entry.Key)
    if found {
        node.Entries[insertPosition] = entry
        return false
    }
    // Insert entry's key in the middle of the node
    node.Entries = append(node.Entries, nil)
    copy(node.Entries[insertPosition+1:], node.Entries[insertPosition:])
    node.Entries[insertPosition] = entry
    tree.split(node)
    return true
}
// insertIntoInternal 
func (tree *Tree) insertIntoInternal(node *Node, entry *Entry) (inserted bool) {
    insertPosition, found := tree.search(node, entry.Key)
    if found {
        node.Entries[insertPosition] = entry
        return false
    }
    return tree.insert(node.Children[insertPosition], entry)
}

你会发现，最终都回到了叶子节点的插入上。

只留下了 insert 相关函数，逻辑关系

splitNonRoot

func (tree *Tree) splitNonRoot(node *Node) {
    middle := tree.middle()
    parent := node.Parent
    left := &Node{Entries: append([]*Entry(nil), node.Entries[:middle]...), Parent: parent}
    right := &Node{Entries: append([]*Entry(nil), node.Entries[middle+1:]...), Parent: parent}
    // Move children from the node to be split into left and right nodes
    if !tree.isLeaf(node) {
        left.Children = append([]*Node(nil), node.Children[:middle+1]...)
        right.Children = append([]*Node(nil), node.Children[middle+1:]...)
        setParent(left.Children, left)
        setParent(right.Children, right)
    }
    insertPosition, _ := tree.search(parent, node.Entries[middle].Key)
    // Insert middle key into parent
    parent.Entries = append(parent.Entries, nil)
    copy(parent.Entries[insertPosition+1:], parent.Entries[insertPosition:])
    parent.Entries[insertPosition] = node.Entries[middle]
    // Set child left of inserted key in parent to the created left node
    parent.Children[insertPosition] = left
    // Set child right of inserted key in parent to the created right node
    parent.Children = append(parent.Children, nil)
    copy(parent.Children[insertPosition+2:], parent.Children[insertPosition+1:])
    parent.Children[insertPosition+1] = right
    tree.split(parent)
}

Remove

直接调用上面的 searchRecursively 即可，内部调用上面提到 search 方法找到删除节点。

// Remove remove the node from the tree by key.
// Key should adhere to the comparator's type assertion, otherwise method panics.
func (tree *Tree) Remove(key interface{}) {
    node, index, found := tree.searchRecursively(tree.Root, key)
    if found {
        tree.delete(node, index)
        tree.size--
    }
}

delete: 一开始我还以为是 Go 内置的函数 delete，仔细一看好像不是。删除某个 Entry 的时候，可能会导致树不再平衡，有些节点可能需要合并。

// delete deletes an entry in node at entries' index
// ref.: https://en.wikipedia.org/wiki/B-tree#Deletion
func (tree *Tree) delete(node *Node, index int) {
    // deleting from a leaf node
    if tree.isLeaf(node) {
        deletedKey := node.Entries[index].Key
        tree.deleteEntry(node, index)
        tree.rebalance(node, deletedKey)
        if len(tree.Root.Entries) == 0 {
            tree.Root = nil
        }
        return
    }
    // deleting from an internal node
    leftLargestNode := tree.right(node.Children[index]) // largest node in the left sub-tree (assumed to exist)
    leftLargestEntryIndex := len(leftLargestNode.Entries) - 1
    node.Entries[index] = leftLargestNode.Entries[leftLargestEntryIndex]
    deletedKey := leftLargestNode.Entries[leftLargestEntryIndex].Key
    tree.deleteEntry(leftLargestNode, leftLargestEntryIndex)
    tree.rebalance(leftLargestNode, deletedKey)
}
// rebalance rebalances the tree after deletion if necessary and returns true, otherwise false.
// Note that we first delete the entry and then call rebalance, thus the passed deleted key as reference.
func (tree *Tree) rebalance(node *Node, deletedKey interface{}) {
    // check if rebalancing is needed
    if node == nil || len(node.Entries) >= tree.minEntries() {
        return
    }
    // try to borrow from left sibling
    leftSibling, leftSiblingIndex := tree.leftSibling(node, deletedKey)
    if leftSibling != nil && len(leftSibling.Entries) > tree.minEntries() {
        // rotate right
        node.Entries = append([]*Entry{node.Parent.Entries[leftSiblingIndex]}, node.Entries...) // prepend parent's separator entry to node's entries
        node.Parent.Entries[leftSiblingIndex] = leftSibling.Entries[len(leftSibling.Entries)-1]
        tree.deleteEntry(leftSibling, len(leftSibling.Entries)-1)
        if !tree.isLeaf(leftSibling) {
            leftSiblingRightMostChild := leftSibling.Children[len(leftSibling.Children)-1]
            leftSiblingRightMostChild.Parent = node
            node.Children = append([]*Node{leftSiblingRightMostChild}, node.Children...)
            tree.deleteChild(leftSibling, len(leftSibling.Children)-1)
        }
        return
    }
    // try to borrow from right sibling
    rightSibling, rightSiblingIndex := tree.rightSibling(node, deletedKey)
    if rightSibling != nil && len(rightSibling.Entries) > tree.minEntries() {
        // rotate left
        node.Entries = append(node.Entries, node.Parent.Entries[rightSiblingIndex-1]) // append parent's separator entry to node's entries
        node.Parent.Entries[rightSiblingIndex-1] = rightSibling.Entries[0]
        tree.deleteEntry(rightSibling, 0)
        if !tree.isLeaf(rightSibling) {
            rightSiblingLeftMostChild := rightSibling.Children[0]
            rightSiblingLeftMostChild.Parent = node
            node.Children = append(node.Children, rightSiblingLeftMostChild)
            tree.deleteChild(rightSibling, 0)
        }
        return
    }
    // merge with siblings
    if rightSibling != nil {
        // merge with right sibling
        node.Entries = append(node.Entries, node.Parent.Entries[rightSiblingIndex-1])
        node.Entries = append(node.Entries, rightSibling.Entries...)
        deletedKey = node.Parent.Entries[rightSiblingIndex-1].Key
        tree.deleteEntry(node.Parent, rightSiblingIndex-1)
        tree.appendChildren(node.Parent.Children[rightSiblingIndex], node)
        tree.deleteChild(node.Parent, rightSiblingIndex)
    } else if leftSibling != nil {
        // merge with left sibling
        entries := append([]*Entry(nil), leftSibling.Entries...)
        entries = append(entries, node.Parent.Entries[leftSiblingIndex])
        node.Entries = append(entries, node.Entries...)
        deletedKey = node.Parent.Entries[leftSiblingIndex].Key
        tree.deleteEntry(node.Parent, leftSiblingIndex)
        tree.prependChildren(node.Parent.Children[leftSiblingIndex], node)
        tree.deleteChild(node.Parent, leftSiblingIndex)
    }
    // make the merged node the root if its parent was the root and the root is empty
    if node.Parent == tree.Root && len(tree.Root.Entries) == 0 {
        tree.Root = node
        node.Parent = nil
        return
    }
    // parent might underflow, so try to rebalance if necessary
    tree.rebalance(node.Parent, deletedKey)
}

看起来好复杂，于是我将它画成一张图

Others

其中迭代器的设计也很优秀，就像 C++ 标准库中的那样，一部分人开发数据结构，一部分人开发算法，通过迭代器来连接。

Reference

B-Tree
[ ] 迭代器的实现
B+ 树的实现