冒泡排序算法

起泡排序 ，别名 冒泡排序 ，该算法的核心思想是将无序表中的所有记录，通过两两比较关键字，得出升序序列或者降序序列。 例如，对无序表 {49，38，65，97，76，13，27，49} 进行升序

起泡排序，别名 “冒泡排序”，该算法的核心思想是将无序表中的所有记录，通过两两比较关键字，得出升序序列或者降序序列。

例如，对无序表{49，38，65，97，76，13，27，49}进行升序排序的具体实现过程如

图

1 所示：

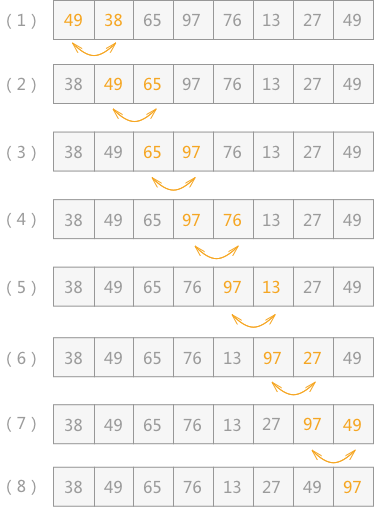
图 1 第一次起泡

如图 1 所示是对无序表的第一次起泡排序，最终将无序表中的最大值 97 找到并存储在表的最后一个位置。具体实现过程为：

1. 首先 49 和 38 比较，由于 38<49，所以两者交换位置，即从（1）到（2）的转变；
2. 然后继续下标为 1 的同下标为 2 的进行比较，由于 49<65，所以不移动位置，（3）中 65 同 97 比较得知，两者也不需要移动位置；
3. 直至（4），97 同 76 进行比较，76<97，两者交换位置，如（5）所示；
4. 同样 97>13（5）、97>27（6）、97>49（7），所以经过一次冒泡排序，最终在无序表中找到一个最大值 97，第一次冒泡结束；

由于 97 已经判断为最大值，所以第二次冒泡排序时就需要找出除 97 之外的无序表中的最大值，比较过程和第一次完全相同。

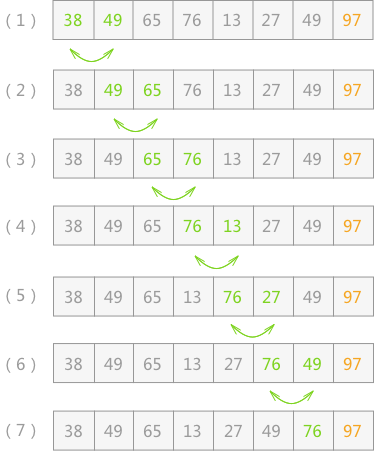
经过第二次冒泡，最终找到了除 97 之外的又一个最大值 76，比较过程完全一样，这里不再描述。

通过一趟趟的比较，一个个的 “最大值” 被找到并移动到相应位置，直到检测到表中数据已经有序，或者比较次数等同于表中含有记录的个数，排序结束，这就是起泡排序。

起泡排序的具体实现代码为：

#include <stdio.h>
void swap(int *a, int *b);
int main()
{
    int array[8] = {49,38,65,97,76,13,27,49};
    int i, j;
    int key;
    for (i = 0; i < 8; i++){
        key=0;
        for (j = 0; j+1<8-i; j++){
            if (array[j] > array[j+1]){
                key=1;
                swap(&array[j], &array[j+1]);
            }
        }
        if (key==0) {
            break;
        }
    }
    for (i = 0; i < 8; i++){
        printf("%d ", array[i]);
    }
    return 0;
}
void swap(int *a, int *b){
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}

js版本

/**
 * @param {array} array
 * @return {array}
 */
var bubbleSort = function(array) {
  const len = array.length;
  for(let i = 0; i < len; i++) {
      let key = 0;
      for(let j = 0; j+1<len-i; j++) {
          if (array[j] > array[j+1]){
                key=1;
                const temp = array[j];
                array[j] = array[j+1];
                array[j+1] = temp;
            }
      }
      if(key === 0) {
          break;
      }
  }
  return array;
}

运行结果为：

13 27 38 49 49 65 76 97

总结

使用起泡排序算法，其时间复杂度同实际表中数据的无序程度有关。若表中记录本身为正序存放，则整个排序过程只需进行 n-1（n 为表中记录的个数）次比较，且不需要移动记录；若表中记录为逆序存放（最坏的情况），则需要 n-1 趟排序，进行 n(n-1)/2 次比较和数据的移动。所以该算法的时间复杂度为O(n2)。