快速排序是由东尼 · 霍尔所发展的一种排序算法。

快速排序是由东尼 · 霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较，但这种状况并不常见。事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

快速排序的名字起的是简单粗暴，因为一听到这个名字你就知道它存在的意义，就是快，而且效率高！它是处理大数据最快的排序算法之一了。虽然 Worst Case 的时间复杂度达到了 O(n²)，但是人家就是优秀，在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好，可是这是为什么呢，我也不知道。好在我的强迫症又犯了，查了 N 多资料终于在《算法艺术与信息学竞赛》上找到了满意的答案：

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

1. 算法步骤

  1. 从数列中挑出一个元素，称为 “基准”（pivot）;
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

2. 动图演示

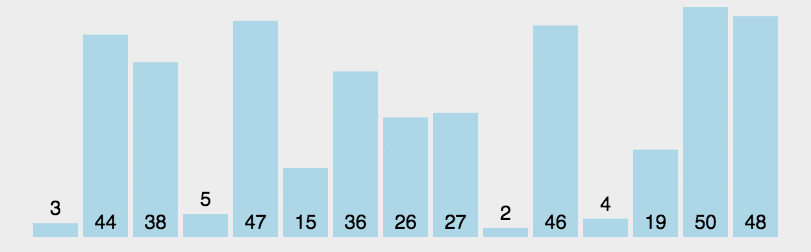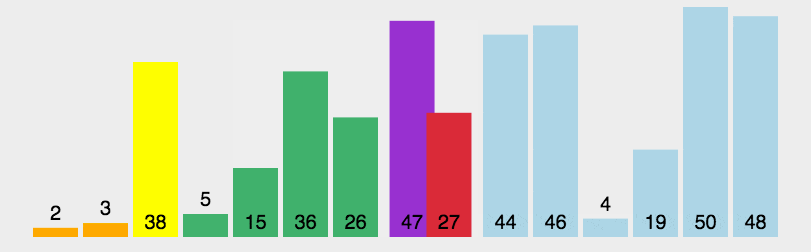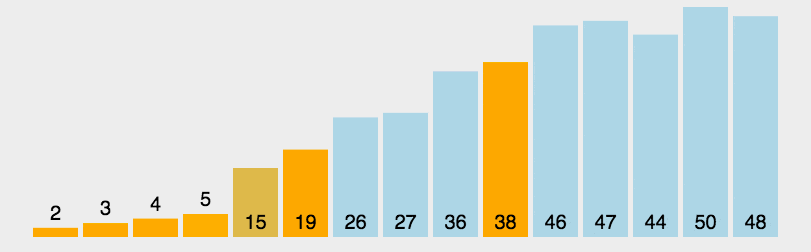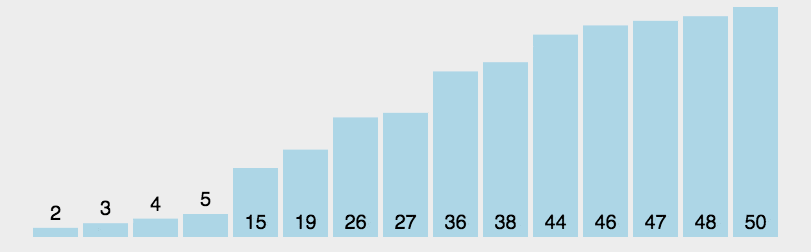
快速排序 - 图1

代码实现

JavaScript

  1. function quickSort(arr, left, right) {
  2.     var len = arr.length,
  3.         partitionIndex,
  4.         left = typeof left != 'number' ? 0 : left,
  5.         right = typeof right != 'number' ? len - 1 : right;
  7.         if (left < right) {
  8.         partitionIndex = partition(arr, left, right);
  9.         quickSort(arr, left, partitionIndex-1);
  10.         quickSort(arr, partitionIndex+1, right);
  11.     }
  12.     return arr;
  13. }
  15. function partition(arr, left ,right) {     // 分区操作
  16.     var pivot = left,                      // 设定基准值（pivot）
  17.         index = pivot + 1;
  18.     for (var i = index; i <= right; i++) {
  19.         if (arr[i] < arr[pivot]) {
  20.             swap(arr, i, index);
  21.             index++;
  22.         }        
  23.     }
  24.     swap(arr, pivot, index - 1);
  25.     return index-1;
  26. }
  28. function swap(arr, i, j) {
  29.     var temp = arr[i];
  30.     arr[i] = arr[j];
  31.     arr[j] = temp;
  32. }
  33. function partition2(arr, low, high) {
  34.   let pivot = arr[low];
  35.   while (low < high) {
  36.     while (low < high && arr[high] > pivot) {
  37.       --high;
  38.     }
  39.     arr[low] = arr[high];
  40.     while (low < high && arr[low] <= pivot) {
  41.       ++low;
  42.     }
  43.     arr[high] = arr[low];
  44.   }
  45.   arr[low] = pivot;
  46.   return low;
  47. }
  49. function quickSort2(arr, low, high) {
  50.   if (low < high) {
  51.     let pivot = partition2(arr, low, high);
  52.     quickSort2(arr, low, pivot - 1);
  53.     quickSort2(arr, pivot + 1, high);
  54.   }
  55.   return arr;
  56. }

Python

  1. def quickSort(arr, left=None, right=None):
  2.     left = 0 if not isinstance(left,(int, float)) else left
  3.     right = len(arr)-1 if not isinstance(right,(int, float)) else right
  4.     if left < right:
  5.         partitionIndex = partition(arr, left, right)
  6.         quickSort(arr, left, partitionIndex-1)
  7.         quickSort(arr, partitionIndex+1, right)
  8.     return arr
  10. def partition(arr, left, right):
  11.     pivot = left
  12.     index = pivot+1
  13.     i = index
  14.     while  i <= right:
  15.         if arr[i] < arr[pivot]:
  16.             swap(arr, i, index)
  17.             index+=1
  18.         i+=1
  19.     swap(arr,pivot,index-1)
  20.     return index-1
  22. def swap(arr, i, j):
  23.     arr[i], arr[j] = arr[j], arr[i]

Go

  1. func quickSort(arr []int) []int {
  2.         return _quickSort(arr, 0, len(arr)-1)
  3. }
  5. func _quickSort(arr []int, left, right int) []int {
  6.         if left < right {
  7.                 partitionIndex := partition(arr, left, right)
  8.                 _quickSort(arr, left, partitionIndex-1)
  9.                 _quickSort(arr, partitionIndex+1, right)
  10.         }
  11.         return arr
  12. }
  14. func partition(arr []int, left, right int) int {
  15.         pivot := left
  16.         index := pivot + 1
  18. for i := index; i <= right; i++ {
  19.         if arr[i] < arr[pivot] {
  20.             swap(arr, i, index)
  21.             index += 1
  22.         }
  23.     }
  24.         swap(arr, pivot, index-1)
  25.         return index - 1
  26. }
  28. func swap(arr []int, i, j int) {
  29.         arr[i], arr[j] = arr[j], arr[i]
  30. }

C++

  1. // 严蔚敏《数据结构》标准分割函数
  2.  Paritition1(int A[], int low, int high) {
  3.    int pivot = A[low];
  4.    while (low < high) {
  5.      while (low < high && A[high] >= pivot) {
  6.        --high;
  7.      }
  8.      A[low] = A[high];
  9.      while (low < high && A[low] <= pivot) {
  10.        ++low;
  11.      }
  12.      A[high] = A[low];
  13.    }
  14.    A[low] = pivot;
  15.    return low;
  16.  }
  18. void QuickSort(int A[], int low, int high) // 快排母函数
  19.  {
  20.    if (low < high) {
  21.      int pivot = Paritition1(A, low, high);
  22.      QuickSort(A, low, pivot - 1);
  23.      QuickSort(A, pivot + 1, high);
  24.    }
  25.  }

Java

  1. public class QuickSort implements IArraySort {
  3. @Override  
  4.     public int[] sort(int[] sourceArray) throws Exception {
  5.         // 对 arr 进行拷贝，不改变参数内容
  6.         int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
  8. return quickSort(arr, 0, arr.length - 1);
  9.     }
  11. private int[] quickSort(int[] arr, int left, int right) {
  12.         if (left < right) {
  13.             int partitionIndex = partition(arr, left, right);
  14.             quickSort(arr, left, partitionIndex - 1);
  15.             quickSort(arr, partitionIndex + 1, right);
  16.         }
  17.         return arr;
  18.     }
  20. private int partition(int[] arr, int left, int right) {
  21.         // 设定基准值（pivot）
  22.         int pivot = left;
  23.         int index = pivot + 1;
  24.         for (int i = index; i <= right; i++) {
  25.             if (arr[i] < arr[pivot]) {
  26.                 swap(arr, i, index);
  27.                 index++;
  28.             }
  29.         }
  30.         swap(arr, pivot, index - 1);
  31.         return index - 1;
  32.     }
  34. private void swap(int[] arr, int i, int j) {
  35.         int temp = arr[i];
  36.         arr[i] = arr[j];
  37.         arr[j] = temp;
  38.     }
  40. }

PHP

  1. function quickSort(arr) <= 1)
  2.         return $arr;
  3.     $middle = $arr[0];
  4.     $leftArray = array();
  5.     $rightArray = array();
  7. for ($i = 1; arr); arr[$i] > $middle)
  8.             $rightArray[] = i];
  9.         else
  10.             $leftArray[] = i];
  11.     }
  12.     leftArray);
  13.     $leftArray[] = $middle;
  15. rightArray);
  16.     return array_merge($leftArray, $rightArray);
  17. }

C

  1. typedef struct _Range {
  2.     int start, end;
  3. } Range;
  5. Range new_Range(int s, int e) {
  6.     Range r;
  7.     r.start = s;
  8.     r.end = e;
  9.     return r;
  10. }
  12. void swap(int x, int y) {
  13.     int t = *x;
  14.     x = y;
  15.     *y = t;
  16. }
  18. void quick_sort(int arr[], const int len) {
  19.     if (len <= 0)
  20.         return; // 避免 len 等於負值時引發段錯誤（Segment Fault）
  21.     // r[] 模擬列表, p 為數量, r[p++] 為 push,r[--p] 為 pop 且取得元素
  22.     Range r[len];
  23.     int p = 0;
  24.     r[p++] = new_Range(0, len - 1);
  25.     while (p) {
  26.         Range range = r[--p];
  27.         if (range.start >= range.end)
  28.             continue;
  29.         int mid = arr[(range.start + range.end) / 2]; // 選取中間點為基準點
  30.         int left = range.start, right = range.end;
  31.         do {
  32.             while (arr[left] < mid) left;   // 檢測基準點左側是否符合要求
  33.             while (arr[right] > mid) --right; // 檢測基準點右側是否符合要求
  34.             if (left <= right) {
  35.                 swap(&arr[left], &arr[right]);
  36.                 left;
  37.                 right--;               // 移動指針以繼續
  38.             }
  39.         } while (left <= right);
  40.         if (range.start < right) r[p++] = new_Range(range.start, right);
  41.         if (range.end > left) r[p++] = new_Range(left, range.end);
  42.     }
  43. }

递归法

  1. void swap(int x, int y) {
  2.     int t = *x;
  3.     x = y;
  4.     *y = t;
  5. }
  7. void quick_sort_recursive(int arr[], int start, int end) {
  8.     if (start >= end)
  9.         return;
  10.     int mid = arr[end];
  11.     int left = start, right = end - 1;
  12.     while (left < right) {
  13.         while (arr[left] < mid && left < right)
  14.             left++;
  15.         while (arr[right] >= mid && left < right)
  16.             right--;
  17.         swap(&arr[left], &arr[right]);
  18.     }
  19.     if (arr[left] >= arr[end])
  20.         swap(&arr[left], &arr[end]);
  21.     else
  22.         left++;
  23.     if (left)
  24.         quick_sort_recursive(arr, start, left - 1);
  25.     quick_sort_recursive(arr, left + 1, end);
  26. }
  28. void quick_sort(int arr[], int len) {
  29.     quick_sort_recursive(arr, 0, len - 1);
  30. }

C++

函数法

  1. sort(a,a + n);// 排序a[0]-a[n-1]的所有数.

迭代法

  1. // 参考：http://www.dutor.net/index.php/2011/04/recursive-iterative-quick-sort/
  2. struct Range {
  3.     int start, end;
  4.     Range(int s = 0, int e = 0) {
  5.         start = s, end = e;
  6.     }
  7. };
  8. template  // 整數或浮點數皆可使用, 若要使用物件 (class) 時必須設定 "小於"(<)、"大於"(>)、"不小於"(>=)的運算子功能
  9. void quick_sort(T arr[], const int len) {
  10.     if (len <= 0)
  11.         return; // 避免 len 等於負值時宣告堆疊陣列當機
  12.     // r[] 模擬堆疊, p 為數量, r[p++] 為 push,r[--p] 為 pop 且取得元素
  13.     Range r[len];
  14.     int p = 0;
  15.     r[p++] = Range(0, len - 1);
  16.     while (p) {
  17.         Range range = r[--p];
  18.         if (range.start >= range.end)
  19.             continue;
  20.         T mid = arr[range.end];
  21.         int left = range.start, right = range.end - 1;
  22.         while (left < right) {
  23.             while (arr[left] < mid && left < right) left++;
  24.             while (arr[right] >= mid && left < right) right--;
  25.             std::swap(arr[left], arr[right]);
  26.         }
  27.         if (arr[left] >= arr[range.end])
  28.             std::swap(arr[left], arr[range.end]);
  29.         else
  30.             left++;
  31.         r[p++] = Range(range.start, left - 1);
  32.         r[p++] = Range(left + 1, range.end);
  33.     }
  34. }

递归法

  1. template 
  2. void quick_sort_recursive(T arr[], int start, int end) {
  3.     if (start >= end)
  4.         return;
  5.     T mid = arr[end];
  6.     int left = start, right = end - 1;
  7.     while (left < right) { // 在整个范围内搜寻比枢纽元值小或大的元素，然后将左侧元素与右侧元素交换
  8.         while (arr[left] < mid && left < right) // 试图在左侧找到一个比枢纽元更大的元素
  9.             left++;
  10.         while (arr[right] >= mid && left < right) // 试图在右侧找到一个比枢纽元更小的元素
  11.             right--;
  12.         std::swap(arr[left], arr[right]); // 交换元素
  13.     }
  14.     if (arr[left] >= arr[end])
  15.         std::swap(arr[left], arr[end]);
  16.     else
  17.         left++;
  18.     quick_sort_recursive(arr, start, left - 1);
  19.     quick_sort_recursive(arr, left + 1, end);
  20. }
  21. template  // 整數或浮點數皆可使用, 若要使用物件 (class) 時必須設定 "小於"(<)、"大於"(>)、"不小於"(>=)的運算子功能
  22. void quick_sort(T arr[], int len) {
  23.     quick_sort_recursive(arr, 0, len - 1);
  24. }

参考地址:

https://github.com/hustcc/JS-Sorting-Algorithm/blob/master/6.quickSort.md

https://zh.wikipedia.org/wiki/快速排序