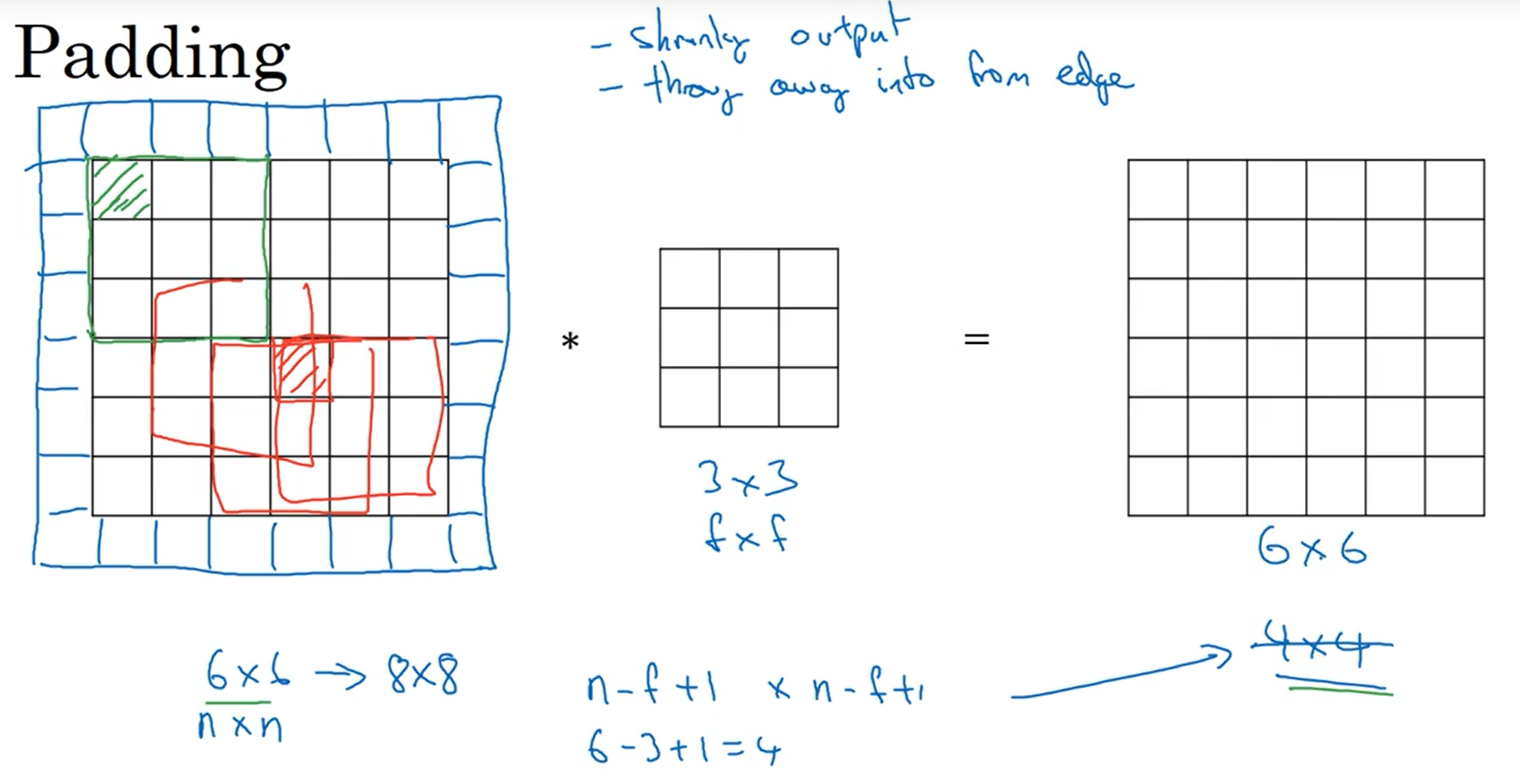
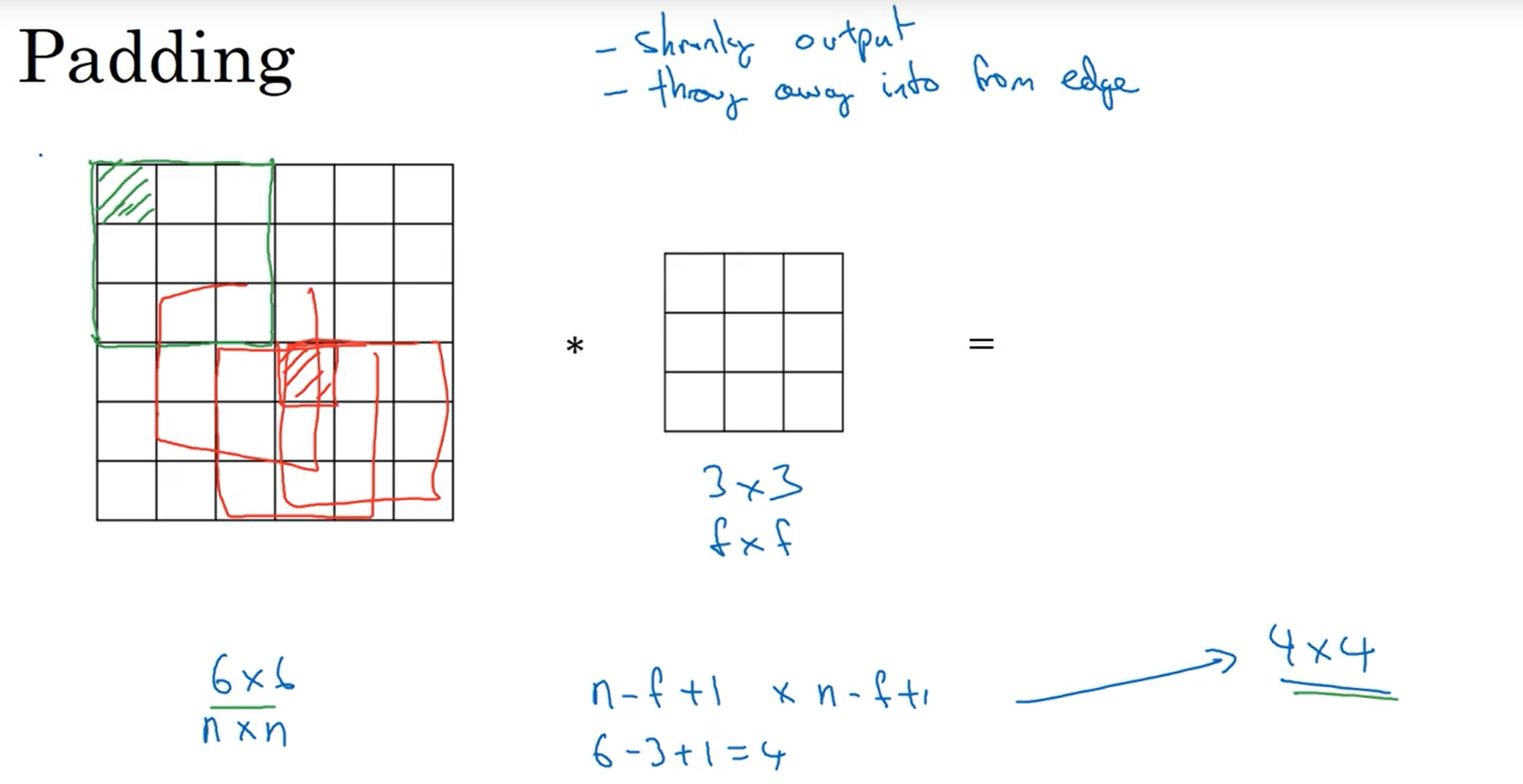
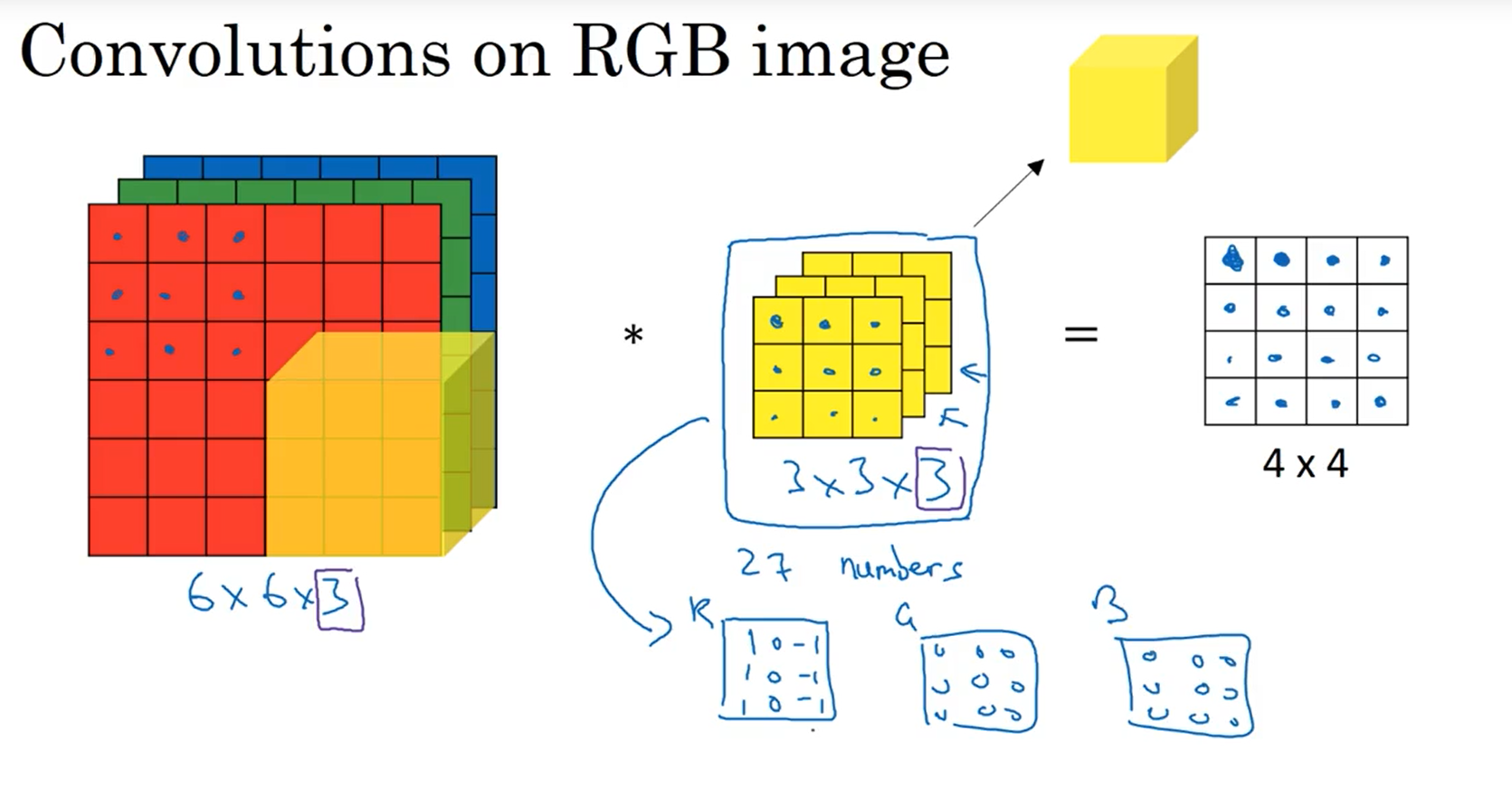
paddingimage.pngimage.pngimage.png

conv on RGB(三维卷积)

image.pngimage.png
note：
输入nnnc(通道数rgb)的图片，用ffnc的卷积核，输出[(n-f+1)][(n-f+1)]Nc(新的通道数，相当于卷积核的数量，也称为神经网络的深度，这里的卷积核是三维卷积)

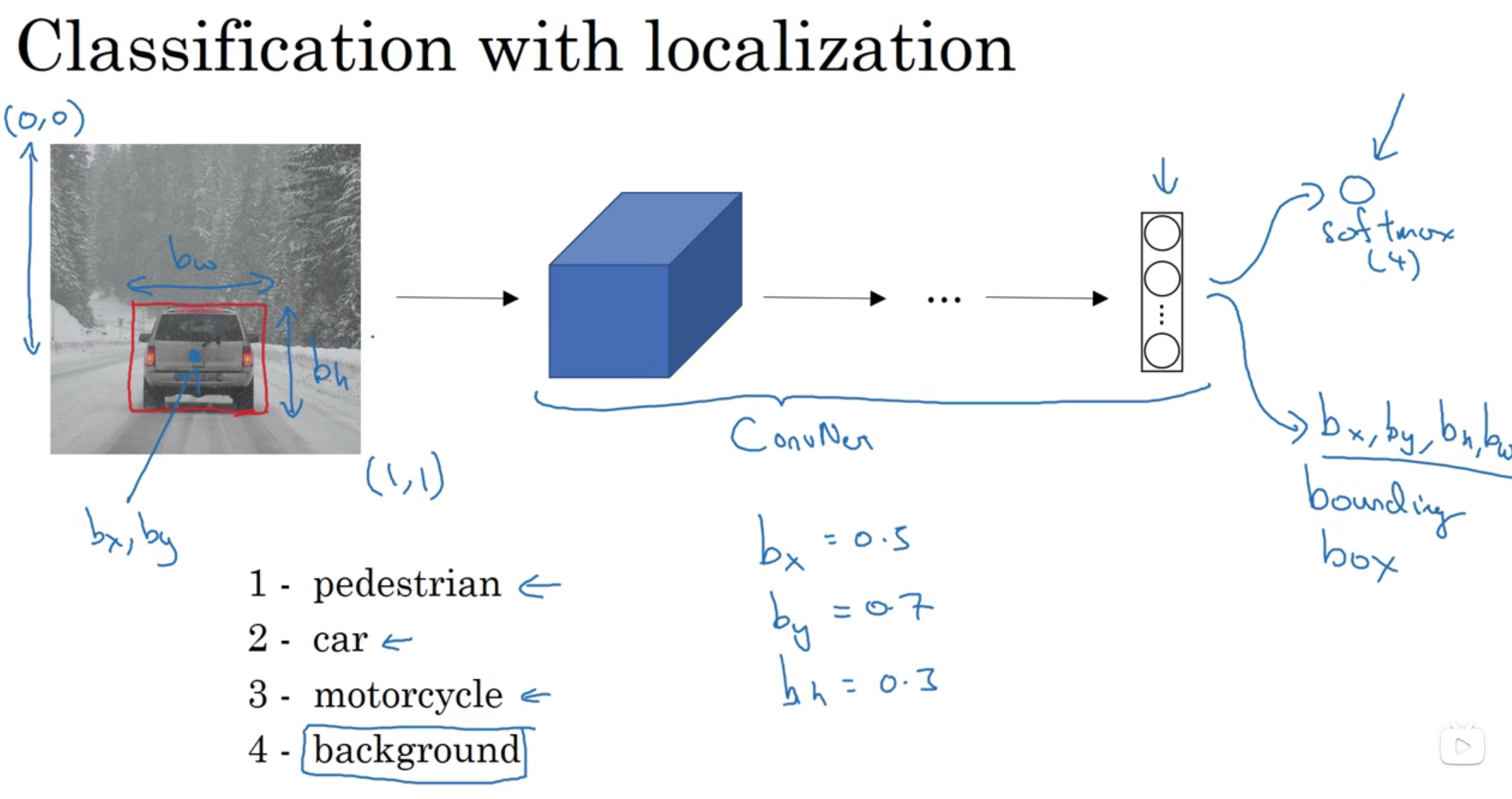
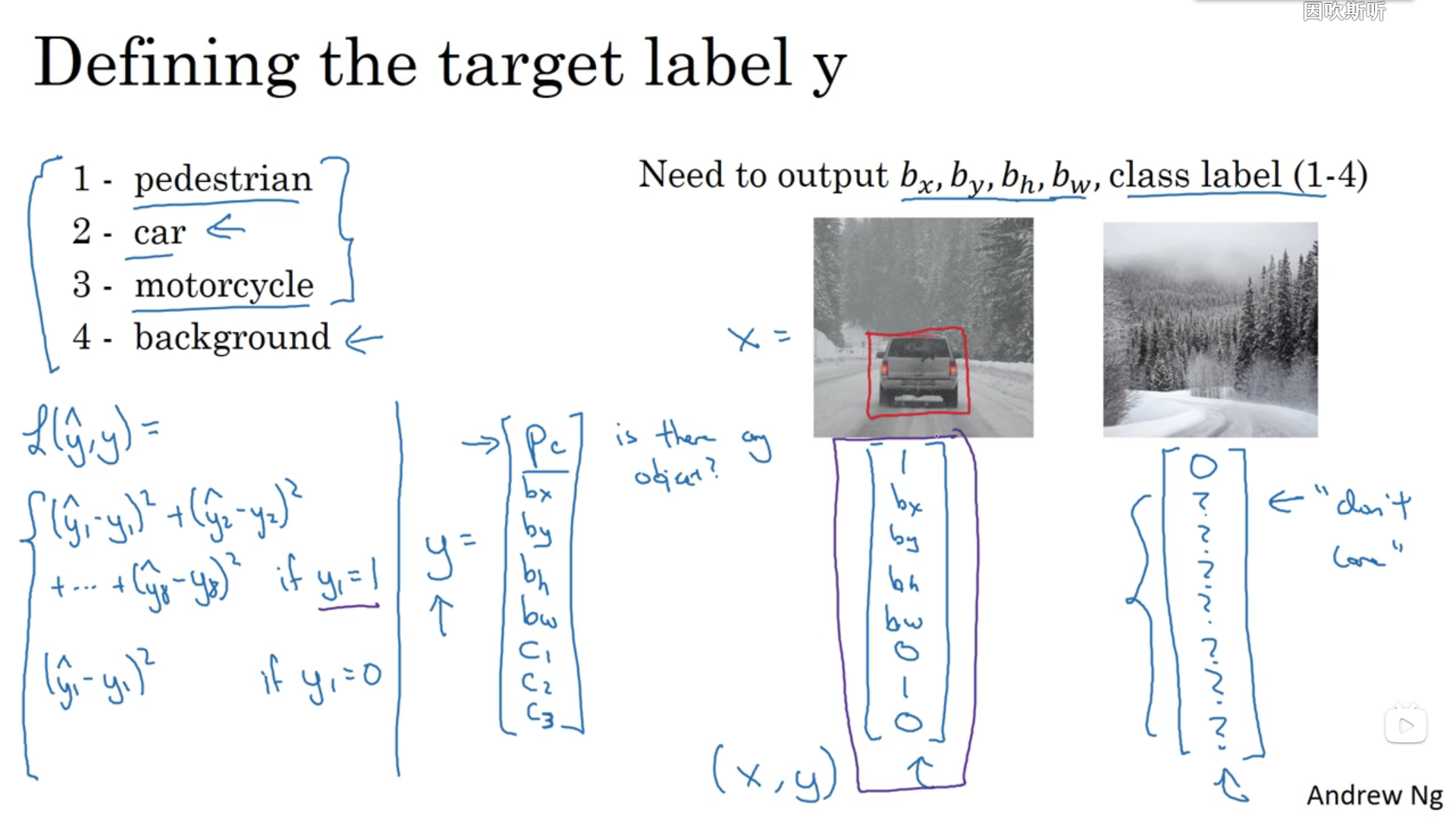
单层卷积网络

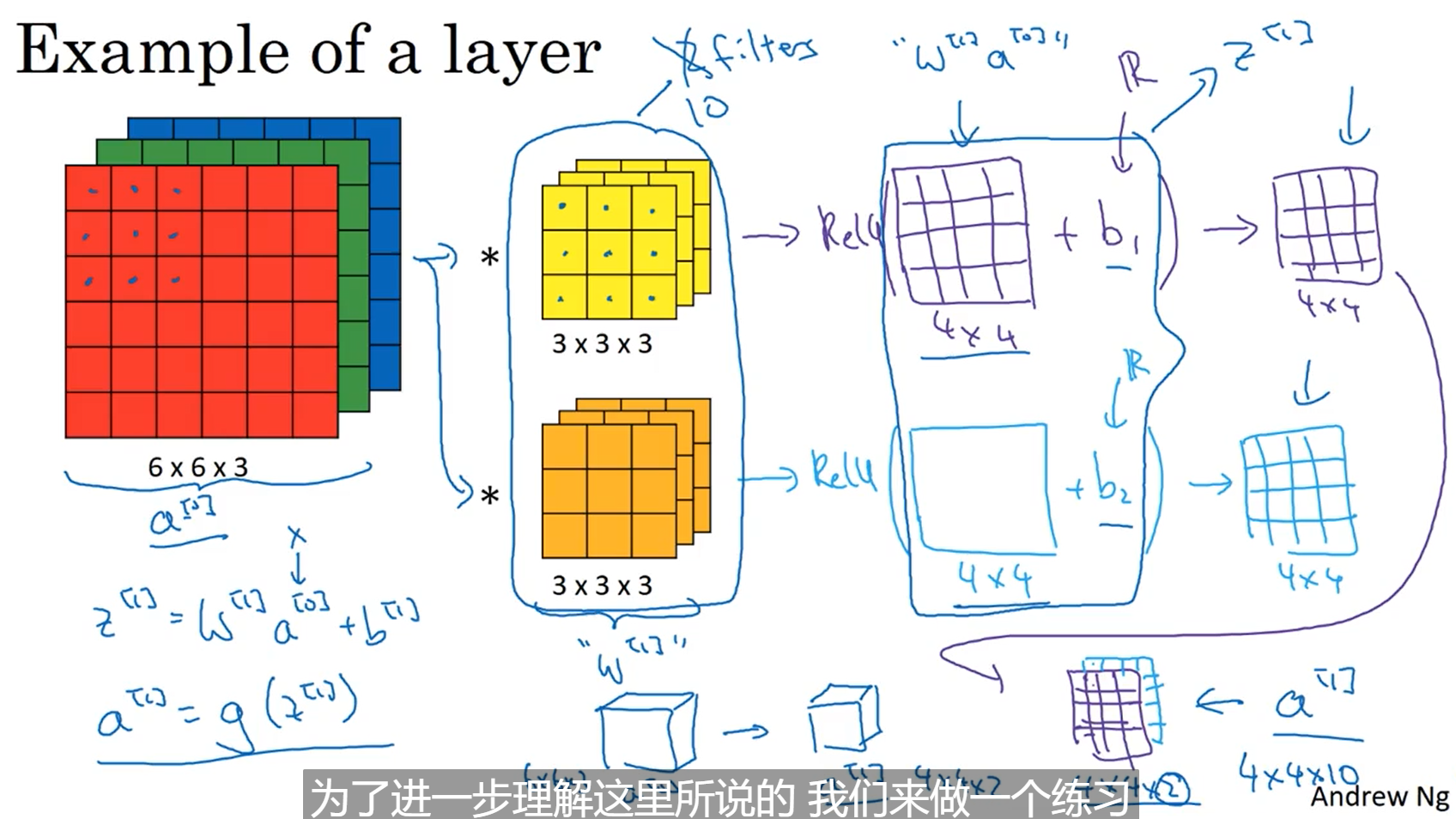
image.png
每个卷积核相当于权重w，而输入的图片为x或者是图中的a，relu(wx+b)是一个通道的计算，最终生成[(n-f+1)/2][(n-f)/s+1]Nc的特征图成为下一层网络的输入也就是下一级的a，这里输入的时候是rgb三个通道，但是经过第一层卷积网之后通道数就变为卷积核的数量，即神经网络的通道数

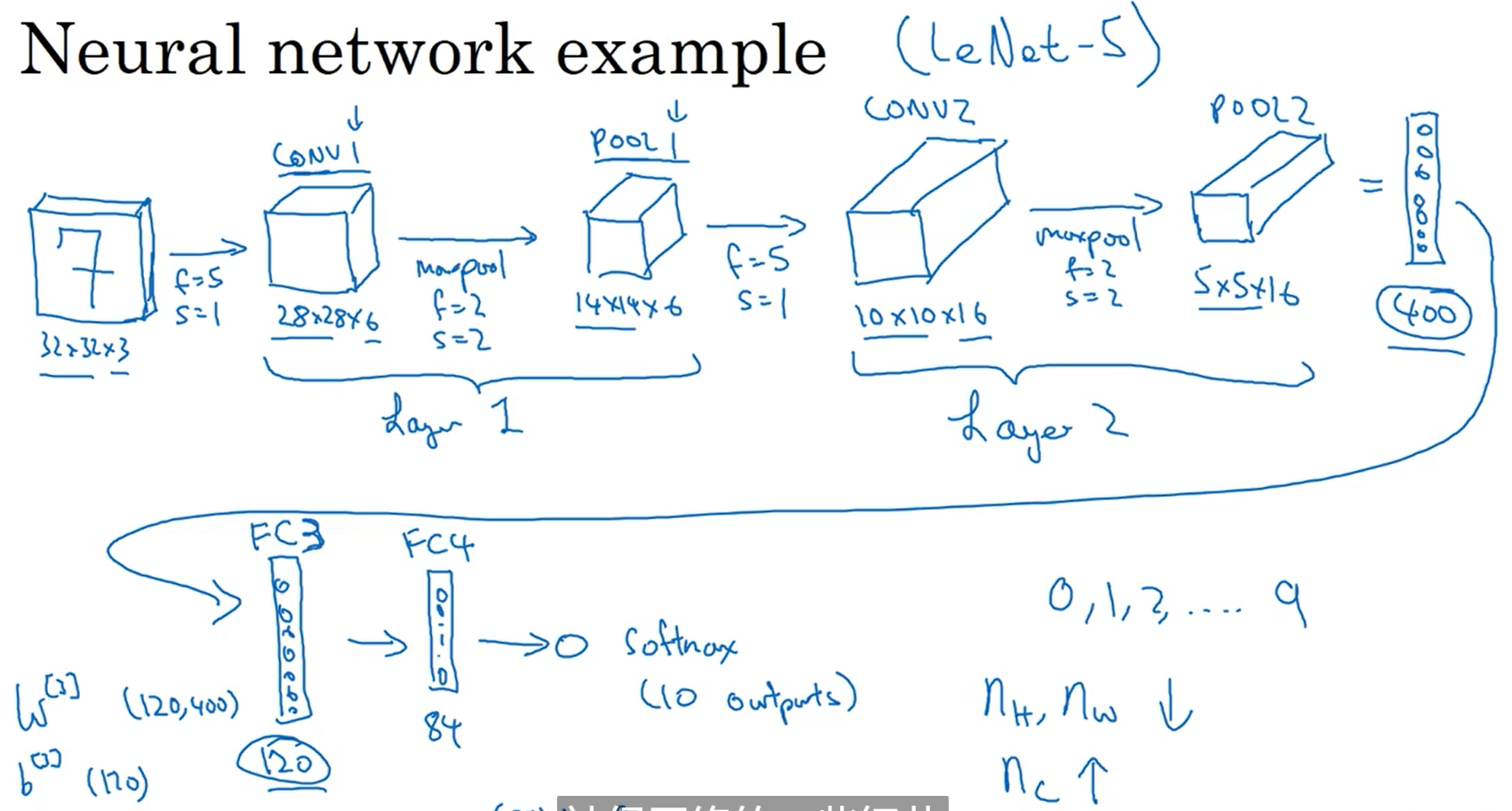
一个简单的卷积网络例子

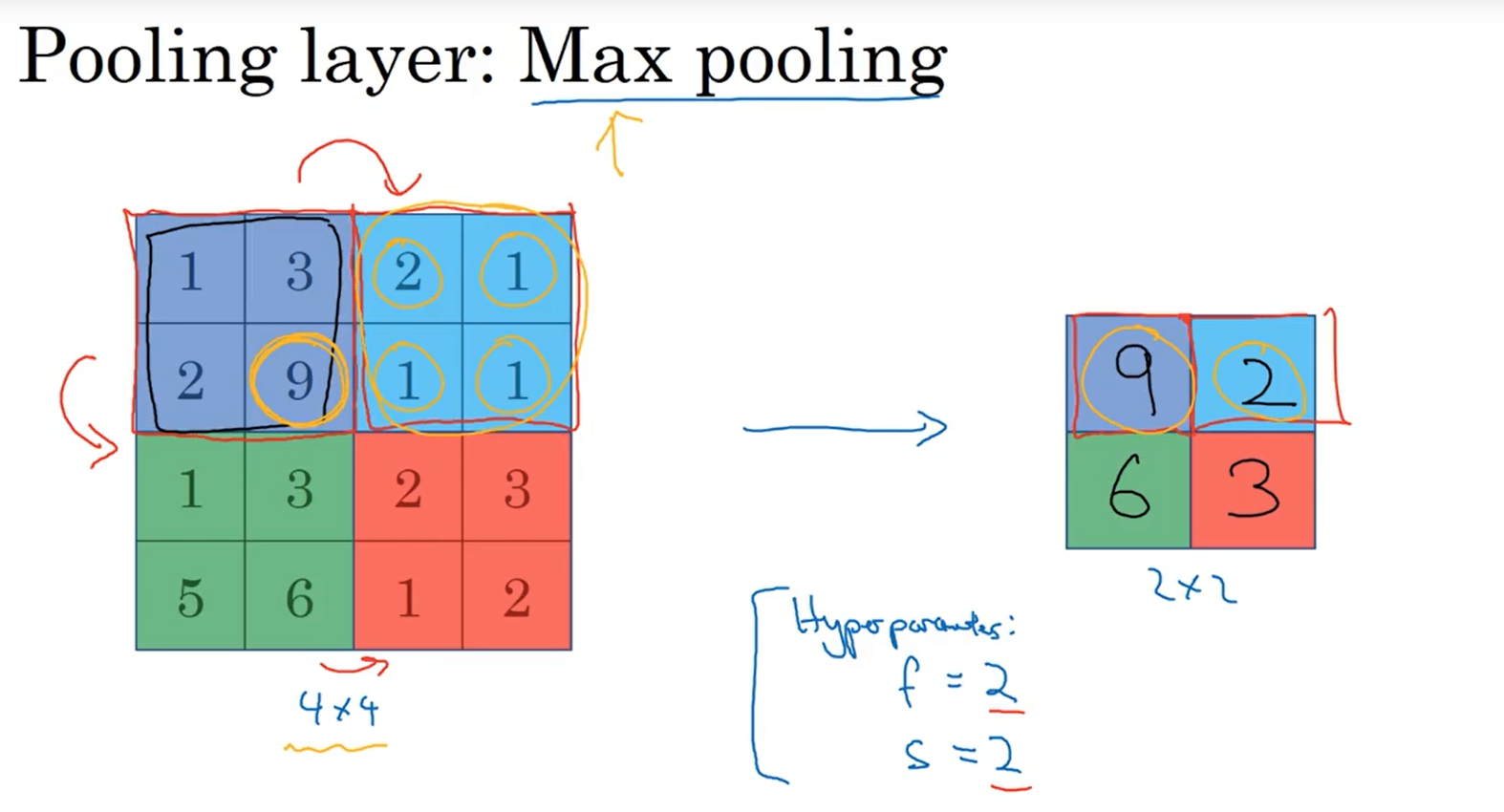
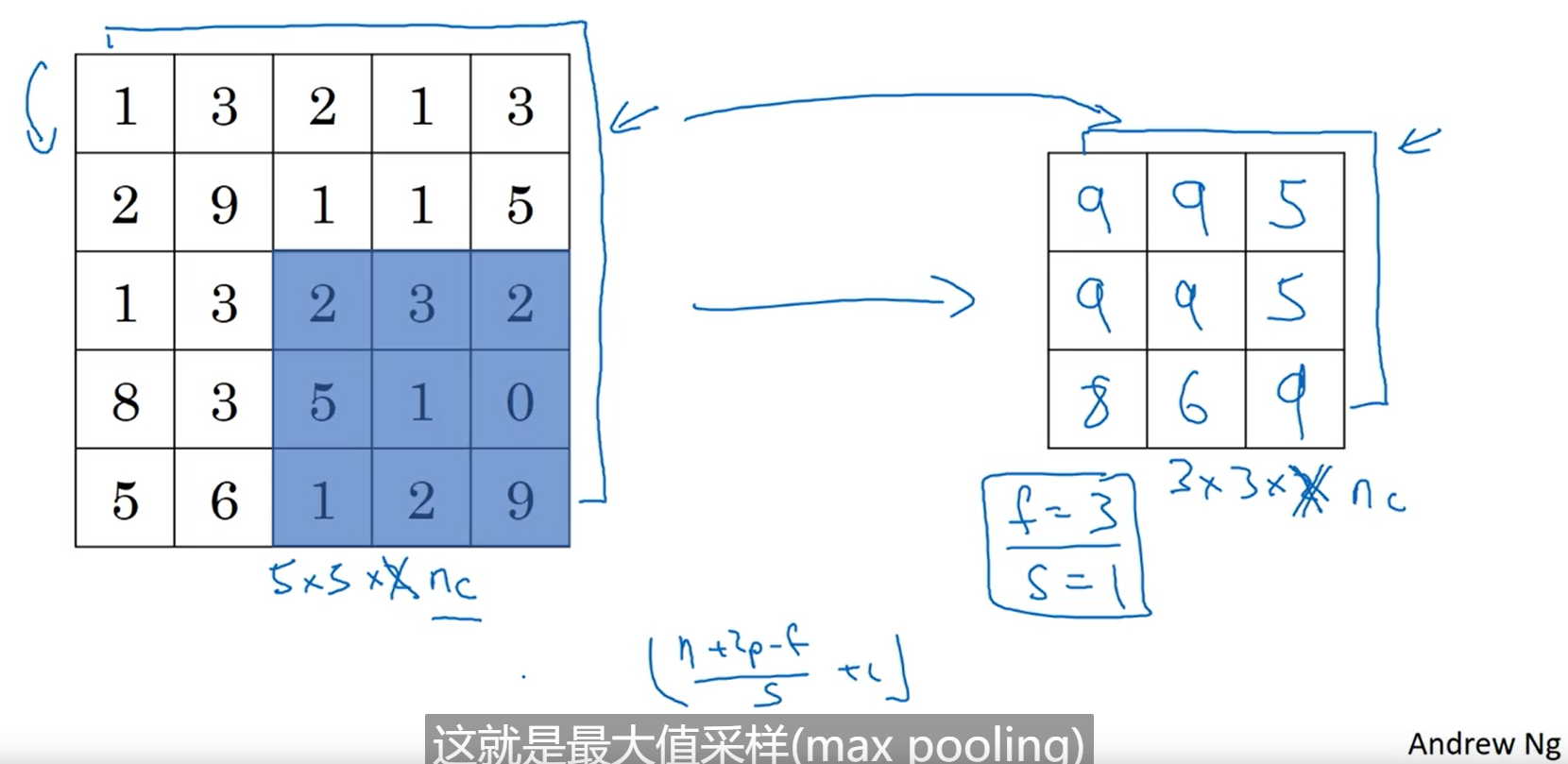
image.png

pooling layer:max pooling

image.pngimage.png

一个复杂的例子

image.png
image.png

经典的网络结构

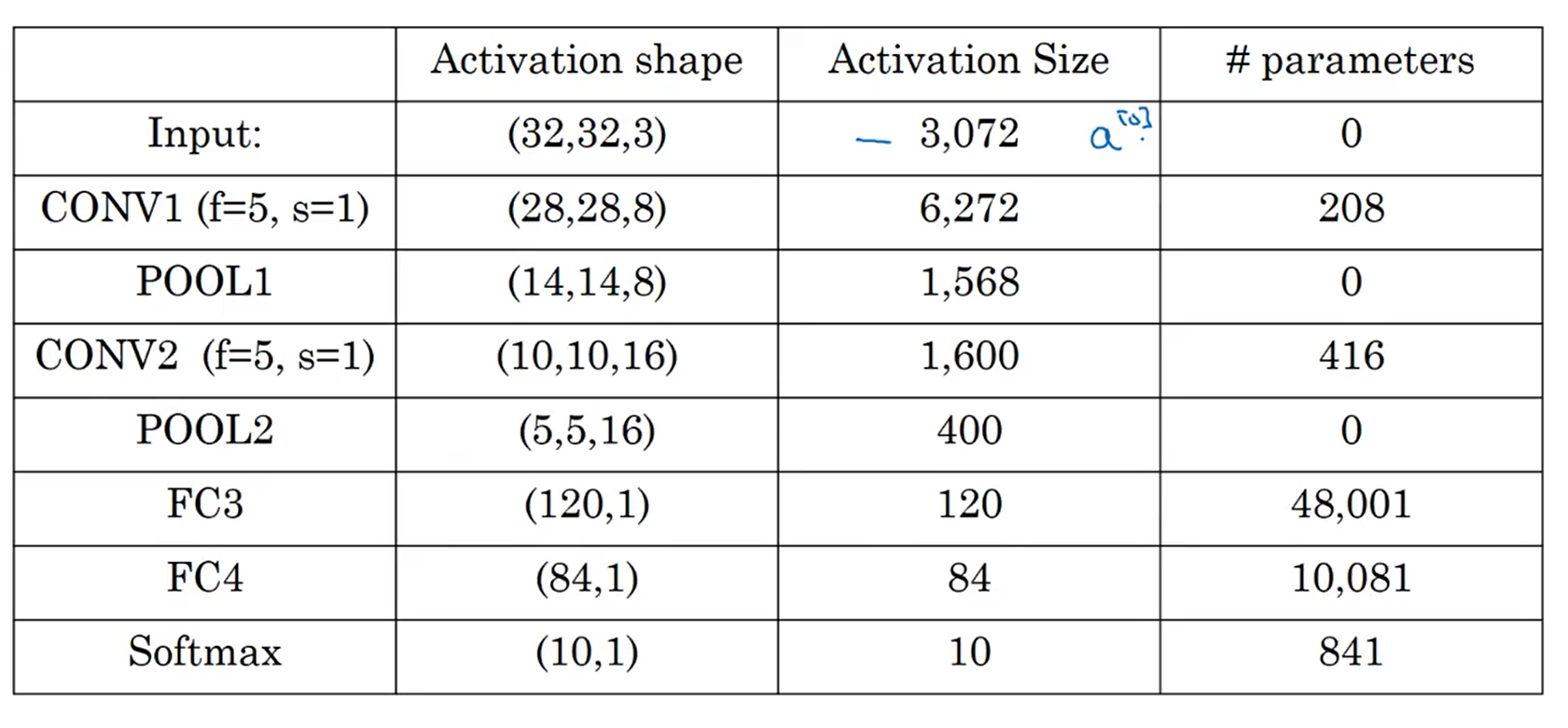
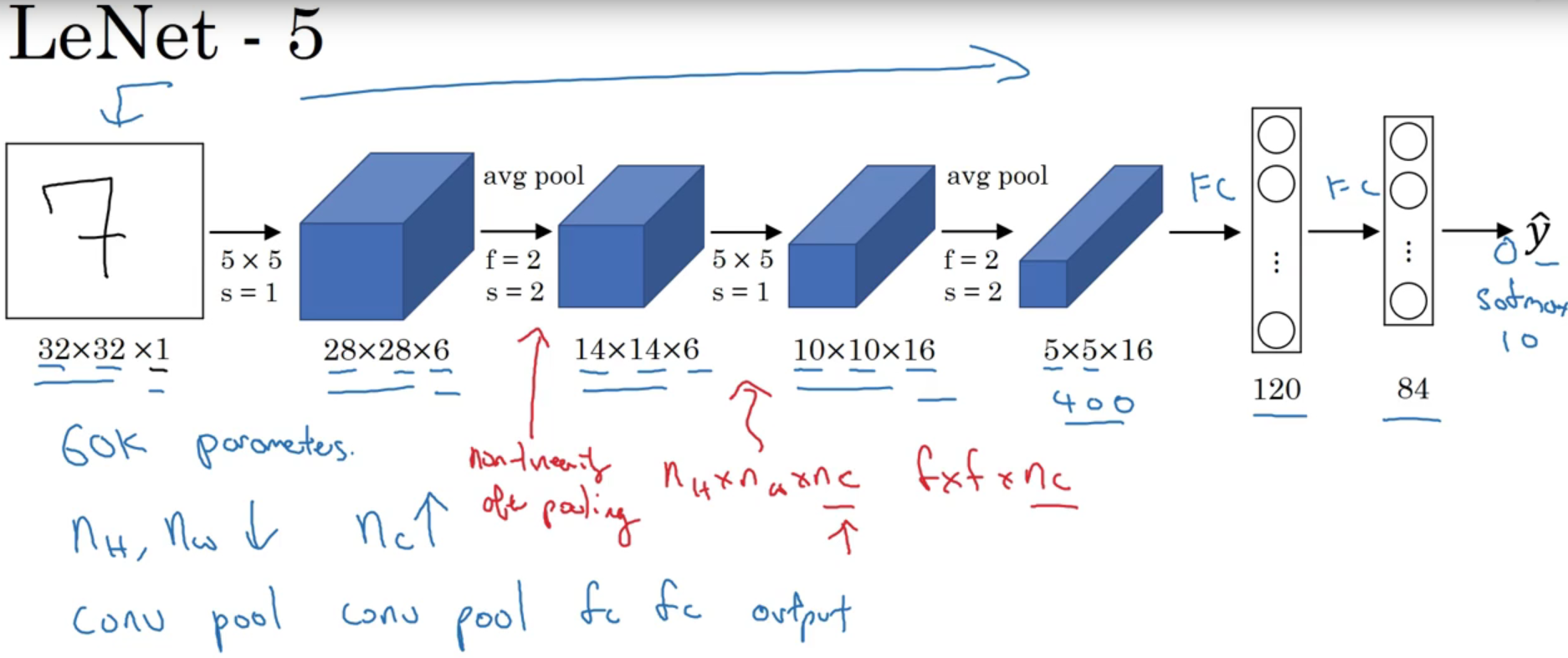
LeNet-5

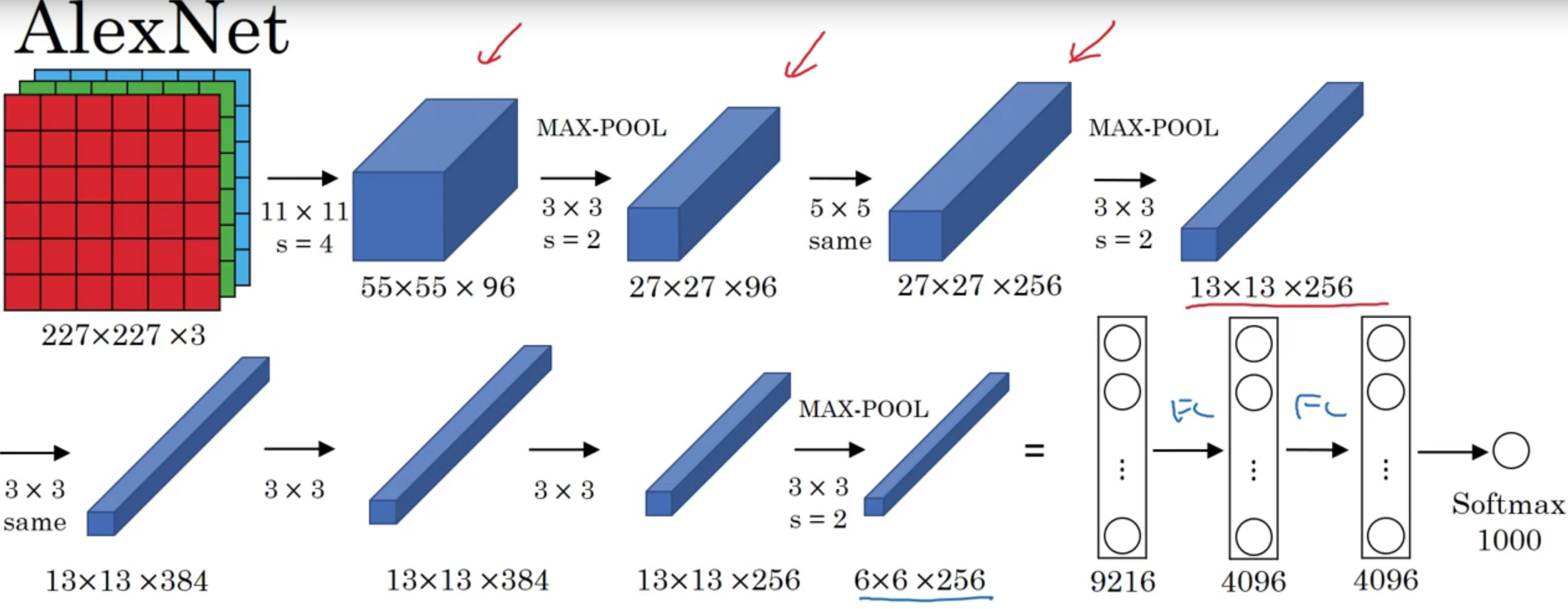
image.png

AlexNet

image.png

VGG-16

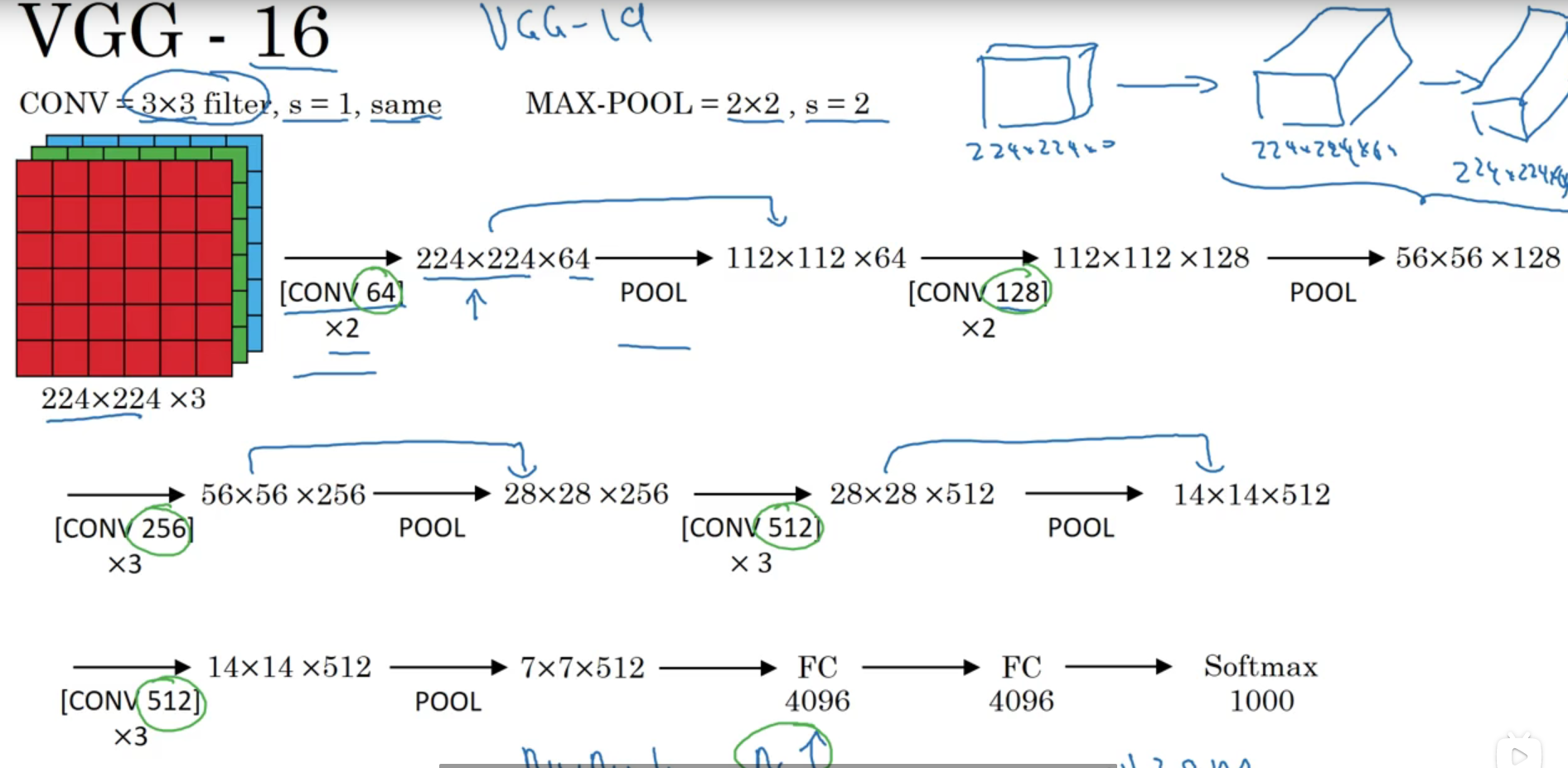
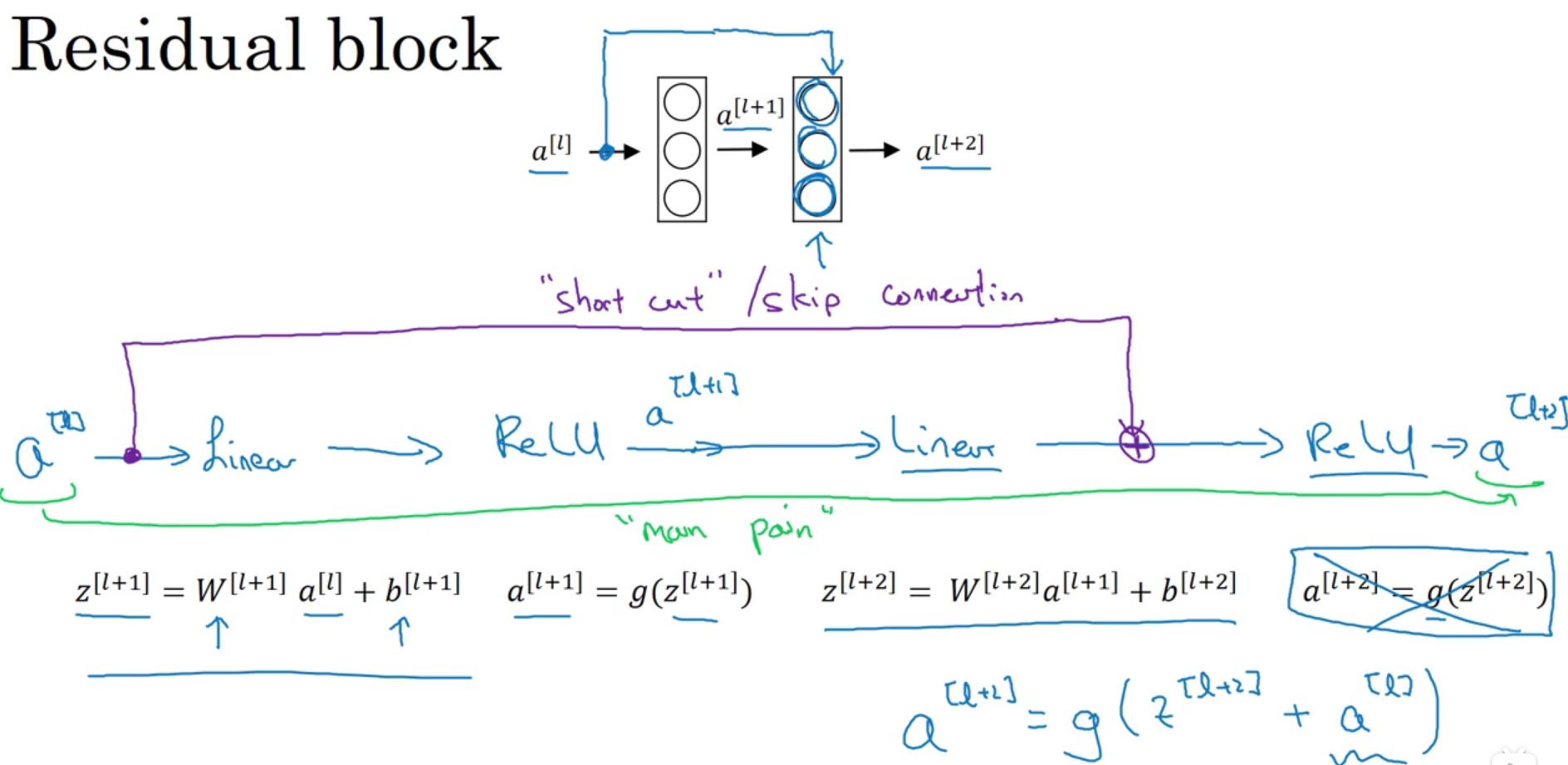
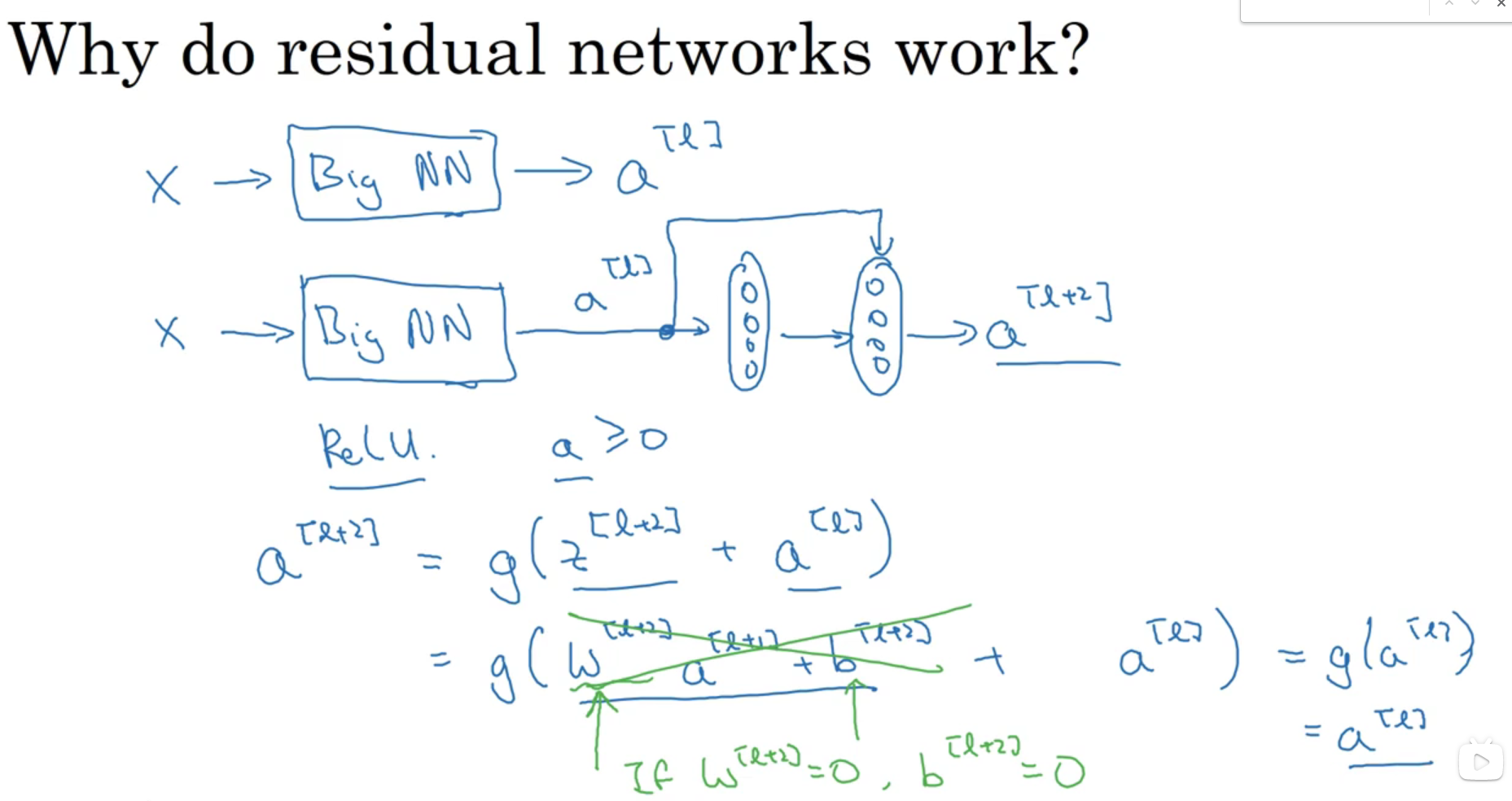
该模型真正的简化了神经网络结构，所有的卷积核都是33，步长为一，并且有padding操作，即same卷积，所有的池化都是22的步长为2image.pngimage.png

ResNet（残差网络）激活以后加前面的特征图

在构建深层网络的时候，理论上网络越深效果越好，但实际上网络越深，出现的错误会越多，这时候训练就很困难，残差网络出现以后使得构建深层网络甚至大于100层的网络成为可能，有人在1000层的网络做了实验，证明了可行性

为什么残差网络有用？

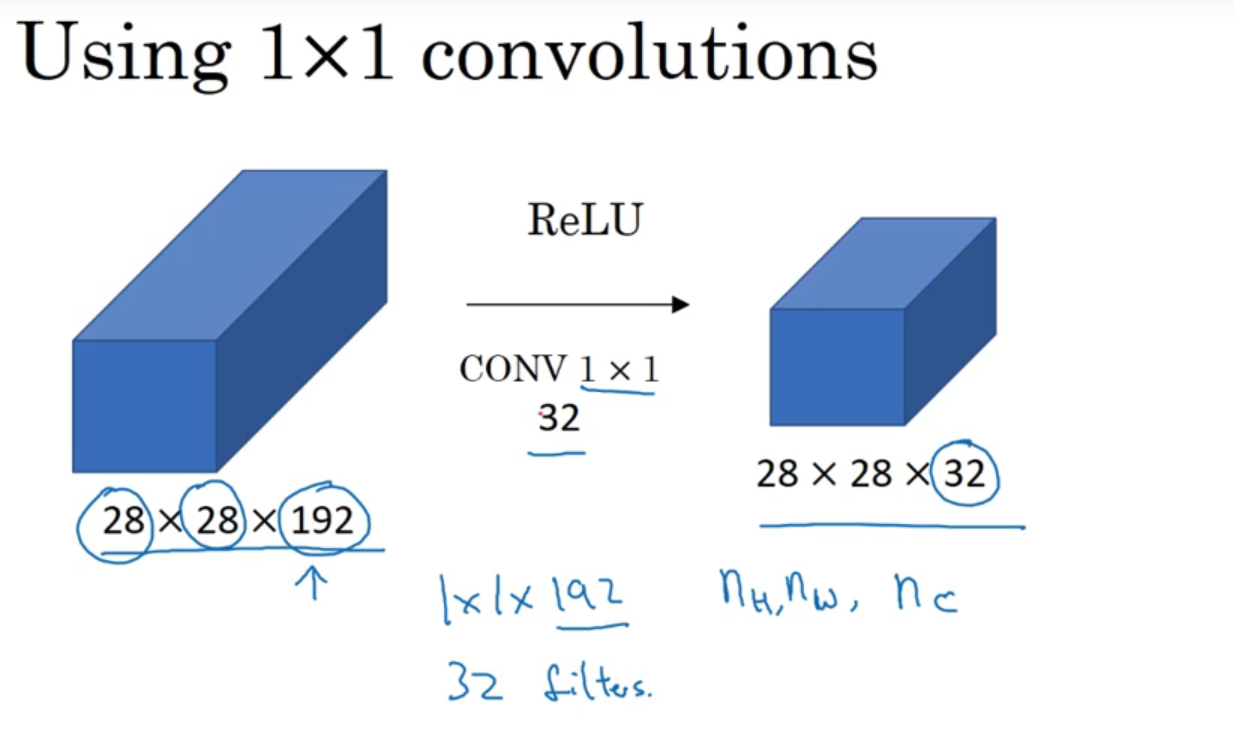
image.png

image.png

网络中的1*1卷积

压缩信道，减小计算量
image.png

Google Inception网络

inception层代替人工来确定卷积核的类型或者确定是否需要创建卷积层或者池化层
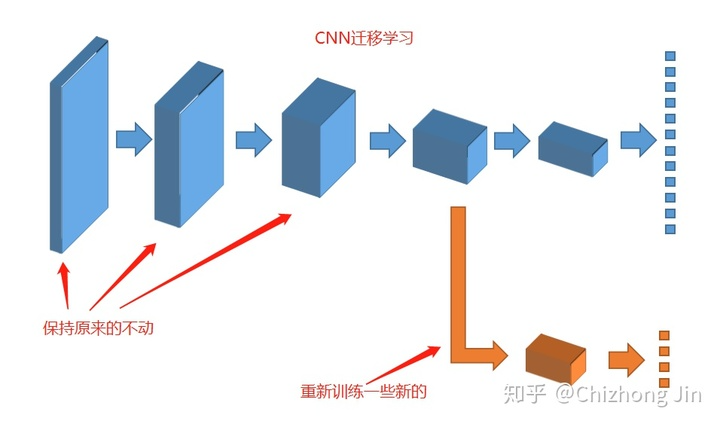
image.png

迁移学习

image.png
Matthew D. Zeiler和Rob Fergus发表了一篇非常著名的论文，阐述卷积神经网络到底“看”到了什么：
image.png
Matthew D. Zeiler和Rob Fergus采用了一种与众不同的思路来解读卷积层的内容。
和对卷积层进行简单的成像不同，他们尝试把不同的内容输入到训练好的神经网络，并观察记录卷积核的激活值。并把造成相同卷积核较大激活的内容分组比较。上面的图片中每个九宫格为同一个卷积核对不同图片的聚类。
在上面图片中可以看出，较浅层的卷积层将较为几何抽象的内容归纳到了一起。例如第一层的卷积中，基本就是边缘检测。而第二层的卷积中，聚类了相似的几何形状，尽管这些几何形状的内容相差甚远。
随着卷积层越来越深，所聚类的内容也越来越具体。例如在第五层里，几乎每个9宫格里都是相同类型的东西。当我们了解了这些“基础知识”后，那么我们有些什么办法可以实现迁移学习？
其实有个最简单易行的方式已经摆在我们面前了：如果我们把卷积神经网络的前n层保留下来，剩下不想要的砍掉怎么样？就像是我们可以不需要ct能识别狗，识别猫，但是轮廓的对我们还是很有帮助的。
image.png

目标定位
image.png

image.png