2-14 update情人节我唯唯诺诺,力扣题我重拳出击
765.情侣牵手 - 困难
题目描述
N 对情侣坐在连续排列的 2N 个座位上,想要牵到对方的手。 计算最少交换座位的次数,以便每对情侣可以并肩坐在一起。 一次交换可选择任意两人,让他们站起来交换座位。
人和座位用 0 到 2N-1 的整数表示,情侣们按顺序编号,第一对是 (0, 1),第二对是 (2, 3),以此类推,最后一对是 (2N-2, 2N-1)。
这些情侣的初始座位 row[i] 是由最初始坐在第 i 个座位上的人决定的。
说明
len(row)是偶数且数值在[4, 60]范围内。- 可以保证
row是序列0...len(row)-1的一个全排列。
题解
很经典的一道并查集的题,理论上把浑坐的组合组成一个并查集,每个并查集的组合数减一之和就是所需要换的最少次数。题解中的时间复杂度是O(NlogN)。
class Solution {public:int getf(vector<int>& f, int x) {if (f[x] == x) {return x;}int newf = getf(f, f[x]);f[x] = newf;return newf;}void add(vector<int>& f, int x, int y) {int fx = getf(f, x);int fy = getf(f, y);f[fx] = fy;}int minSwapsCouples(vector<int>& row) {int n = row.size();int tot = n / 2;vector<int> f(tot, 0);for (int i = 0; i < tot; i++) {f[i] = i;}for (int i = 0; i < n; i += 2) {int l = row[i] / 2;int r = row[i + 1] / 2;add(f, l, r);}unordered_map<int, int> m;for (int i = 0; i < tot; i++) {int fx = getf(f, i);m[fx]++;}int ret = 0;for (const auto& [f, sz]: m) {ret += sz - 1;}return ret;}};
另外,题解中还提供了一种广度优先搜索的方法,复杂度被控制到了O(N):
class Solution {
public:
int minSwapsCouples(vector<int>& row) {
int n = row.size();
int tot = n / 2;
vector<vector<int>> graph(tot);
for (int i = 0; i < n; i += 2) {
int l = row[i] / 2;
int r = row[i + 1] / 2;
if (l != r) {
graph[l].push_back(r);
graph[r].push_back(l);
}
}
vector<int> visited(tot, 0);
int ret = 0;
for (int i = 0; i < tot; i++) {
if (visited[i] == 0) {
queue<int> q;
visited[i] = 1;
q.push(i);
int cnt = 0;
while (!q.empty()) {
int x = q.front();
q.pop();
cnt += 1;
for (int y: graph[x]) {
if (visited[y] == 0) {
visited[y] = 1;
q.push(y);
}
}
}
ret += cnt - 1;
}
}
return ret;
}
};
这种方法的思路其实和上面的并查集类似,就是先检测每个节点,看与之相邻的是否为正确的组合,如果不是,就保存他的跳跃之后的组合位置,之后的visit就计算组合跳跃次数减一。
其实核心思想都是不管怎么交换,最少次数的交换都是混乱链接的组合数减一。
题有点意思,记录一下。
今天的每日一题:传送门
TODO: 此外,这道题还有一种算法叫佛洛伊德算法,我还没有仔细研究,等到什么时候复盘这篇题解,再回来研究这个
题目描述
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0替代这个答案。
提示
1 <= equations.length <= 20equations[i].length == 21 <= Ai.length, Bi.length <= 5values.length == equations.length0.0 < values[i] <= 20.01 <= queries.length <= 20queries[i].length == 21 <= Cj.length, Dj.length <= 5Ai, Bi, Cj, Dj由小写英文字母与数字组成
输入输出样例
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果
我的思路
初看起来没什么好的思路,是打算用笨方法做模拟,给第一个数字设置初值1,之后都是他的倍数,但是马上想到,万一有两条单独的链,最后两个节点合并时,是很麻烦的(得有一条链递归的改回去)
这就想到了并查集,但是具体思路就不会了(我tm算法和数据结构到底学了啥……
~~
于是就是查看题解:
题解
由于 变量之间的倍数关系具有传递性,处理有传递性关系的问题,可以使用「并查集」,我们需要在并查集的「合并」与「查询」操作中 维护这些变量之间的倍数关系。
说明:请大家注意看一下题目中的「注意」和「数据范围」,例如:每个 Ai 或 Bi 是一个表示单个变量的字符串。所以用例 equation = [“ab”, “cd”] ,这里的 ab 视为一个变量,不表示 a * b。如果面试中遇到这样的问题,一定要和面试官确认清楚题目的条件。还有 1 <= equations.length <= 20 和 values[i] > 0.0 可以避免一些特殊情况的讨论。
方法:并查集
分析示例 :
- a / b = 2.0 说明 a = 2ba=2b, a 和 b 在同一个集合中;
- b / c = 3.0 说明 b = 3cb=3c ,b 和 c 在同一个集合中。

我们计算了两个结果,不难知道:可以将题目给出的 equation 中的两个变量所在的集合进行「合并」,同在一个集合中的两个变量就可以通过某种方式计算出它们的比值。具体来说,可以把不同的变量的比值转换成为相同的变量的比值,这样在做除法的时候就可以消去相同的变量,然后再计算转换成相同变量以后的系数的比值,就是题目要求的结果。统一了比较的标准,可以以 O(1) 的时间复杂度完成计算。
如果两个变量不在同一个集合中, 返回 -1.0。并且根据题目的意思,如果两个变量中至少有一个 变量没有出现在所有 equations 出现的字符集合中,也返回 -1.0−1.0。
构建有向图
通过例子的分析,我们就知道了,题目给出的 equations 和 values 可以表示成一个图,equations 中出现的变量就是图的顶点,「分子」于「分母」的比值可以表示成一个有向关系(因为「分子」和「分母」是有序的,不可以对换),并且这个图是一个带权图,values 就是对应的有向边的权值。
统一变量和路径压缩关系
刚刚在分析例子的过程中,提到了:可以把一个一个 query 中的不同变量转换成同一个变量,这样在计算 query 的时候就可以以 O(1) 的时间复杂度计算出结果,在「并查集」的一个优化技巧中,「路径压缩」就恰好符合了这样的应用场景。
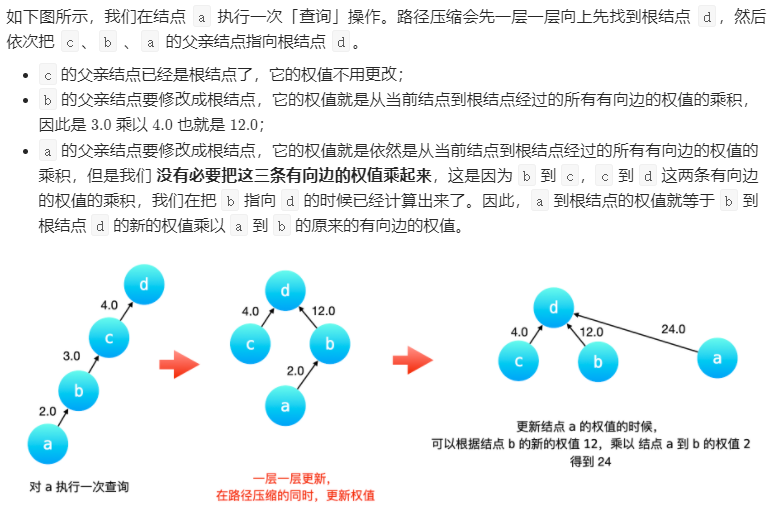
为了避免并查集所表示的树形结构高度过高,影响查询性能。「路径压缩」就是针对树的高度的优化。「路径压缩」的效果是:在查询一个结点 a 的根结点同时,把结点 a 到根结点的沿途所有结点的父亲结点都指向根结点。特别地,也可以认为根结点的父亲结点就是根结点自己。
由于有「路径压缩」的优化,两个同在一个连通分量中的不同的变量,它们分别到根结点(父亲结点)的权值的比值,就是题目的要求的结果。
在路径压缩中维护权值变化
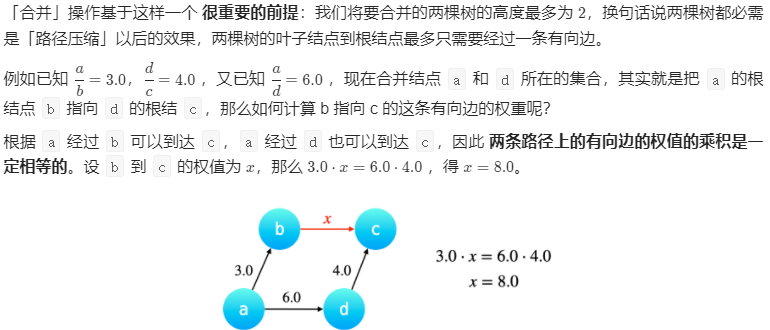
在合并中维护权值变化
复杂度分析

代码:
class Solution {
public:
int findf(vector<int>& f, vector<double>& w, int x) {
if (f[x] != x) {
int father = findf(f, w, f[x]);
w[x] = w[x] * w[f[x]];
f[x] = father;
}
return f[x];
}
void merge(vector<int>& f, vector<double>& w, int x, int y, double val) {
int fx = findf(f, w, x);
int fy = findf(f, w, y);
f[fx] = fy;
w[fx] = val * w[y] / w[x];
}
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
int nvars = 0;
unordered_map<string, int> variables;
int n = equations.size();
for (int i = 0; i < n; i++) {
if (variables.find(equations[i][0]) == variables.end()) {
variables[equations[i][0]] = nvars++;
}
if (variables.find(equations[i][1]) == variables.end()) {
variables[equations[i][1]] = nvars++;
}
}
vector<int> f(nvars);
vector<double> w(nvars, 1.0);
for (int i = 0; i < nvars; i++) {
f[i] = i;
}
for (int i = 0; i < n; i++) {
int va = variables[equations[i][0]], vb = variables[equations[i][1]];
merge(f, w, va, vb, values[i]);
}
vector<double> ret;
for (const auto& q: queries) {
double result = -1.0;
if (variables.find(q[0]) != variables.end() && variables.find(q[1]) != variables.end()) {
int ia = variables[q[0]], ib = variables[q[1]];
int fa = findf(f, w, ia), fb = findf(f, w, ib);
if (fa == fb) {
result = w[ia] / w[ib];
}
}
ret.push_back(result);
}
return ret;
}
};
相似练习
「力扣」第 547 题:省份数量(中等);
「力扣」第 684 题:冗余连接(中等);
「力扣」第 1319 题:连通网络的操作次数(中等);
「力扣」第 1631 题:最小体力消耗路径(中等);
「力扣」第 959 题:由斜杠划分区域(中等);
get
「力扣」第 947 题:移除最多的同行或同列石头(中等);
「力扣」第 721 题:账户合并(中等);
「力扣」第 803 题:打砖块(困难);
「力扣」第 1579 题:保证图可完全遍历(困难);
「力扣」第 778 题:水位上升的泳池中游泳(困难)。
1-11 update
今天的题目:「力扣」第 1202 题:交换字符串中的元素(中等);
本来是用c++的stl的一道题,评论区看到大佬的c版本,感觉思路很巧妙,贴上我稍微修改之后的版本:
int find(int* list, int i){
if(list[i] == i) return i;
else{
list[i] = find(list, list[i]);
return list[i];
}
}
inline void Union(int* list, int i, int j){
if(find(list, i) != find(list, j)){
list[find(list, i)] = find(list, j);
}
else return;
}
char take(int* list){
for(int i = 0; i < 26; i++){
if(list[i]){
list[i]--;
return i + 'a';
}
}
return 0;
}
char * smallestStringWithSwaps(char * s, int** pairs, int pairsSize, int* pairsColSize){
int len = strlen(s);
int list[len];
for(int i = 0; i < len; i++){
list[i] = i;
}
for(int i = 0; i < pairsSize; i++){
int a = pairs[i][0], b = pairs[i][1];
Union(list, a, b);
}
int rebuild[len][26];
memset(rebuild, 0, sizeof(rebuild));
for(int i = 0; i < len; i++){
rebuild[find(list,i)][s[i] - 'a']++;
}
for(int i = 0; i < len; i++){
s[i] = take(rebuild[find(list,i)]);
}
return s;
}
(主要是修改了大佬奇怪的Union部分,感觉他写的很罗嗦,不过改完之后时间多了几十ms,QAQ)

