校验与纠错

码距

码距：两个码字中不同的二进制位数
例如： 这两个码字，0011 和 0101 的码距是 2

编码系统的码距：整个编码系统中任意两个字符的最小码距

检测与纠错需要的码距

为什么是这样？

要检测 D 位的错误，编码系统的码距至少为 D + 1
要纠错 D 位的错误，编码系统的码距至少位 2D + 1

例如：使用 3 个二进制位来编码 4 个码字：
001 010 100 111
可以计算出这个编码的码距为 2，可以检测 1 位错误，无法进行纠错

奇偶校验码这种编码方式，码距为 2，可以检测 1 为错误，无法纠错
海明码这种编码方式，码距为 3，可以发现 2 位错误，或者纠正 1 位错误

奇偶校验码

奇偶校验包含奇校验和偶校验两种校验方式，收发双方需要商定使用哪一种。

校验原理
以奇校验为例。在附加一位校验码后，比特流中 1 的个数一定是奇数。

检测能力
只有当奇数个 bit 同时发生了翻转时，奇偶校验才能检测到错误；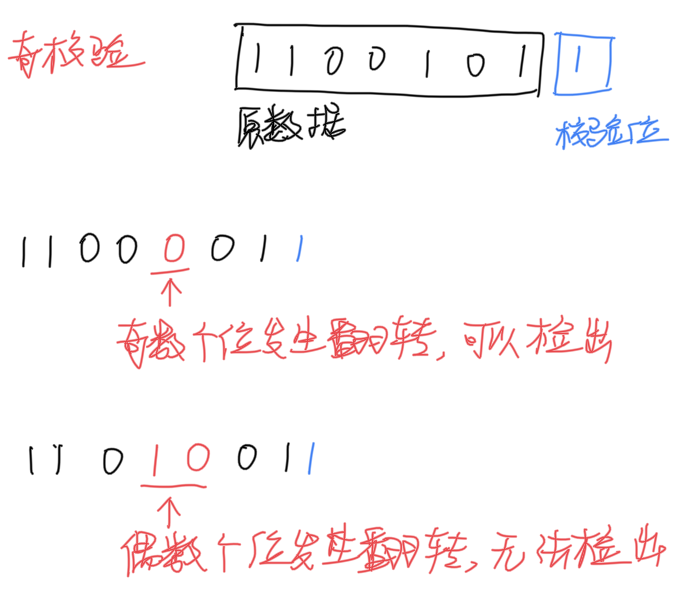

CRC 校验码

二进制数表示多项式：将二进制数的每一位视为多项式的系数，则一个二进制数可以表示一个多项式。 例如： 1101 表示的多项式为： 注意，多项式有常数项，其与二进制数的最低位相对应。

校验原理
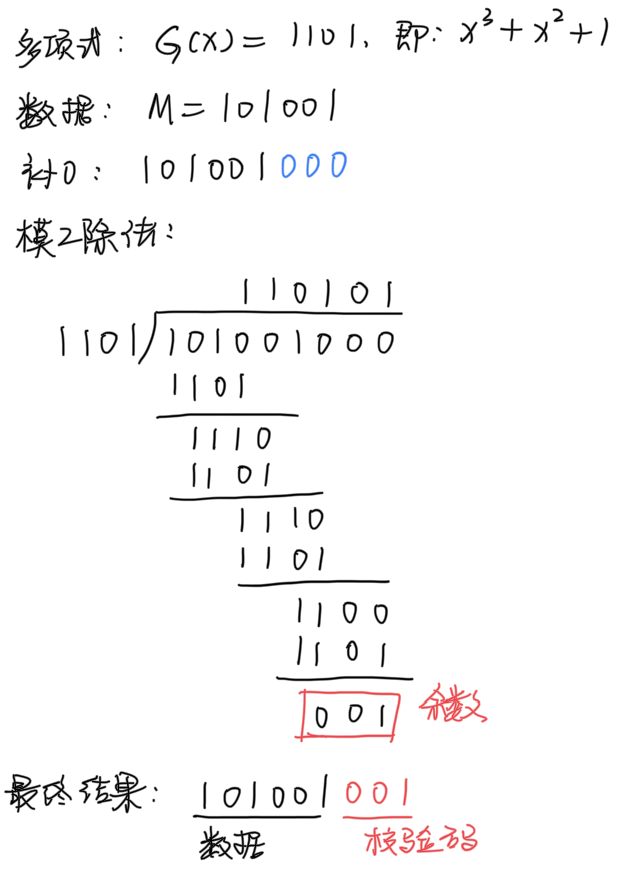
收发双方首先确定一个多项式 G(x) 。
发送方计算出校验码，将校验码附加在信息后面发送给接收方。
接收方用收到的比特流除以表示多项式的二进制串 ，如果能够整除，说明没有错误。

多项式的选择
多项式的最高位和最低位必须是 1。（即，多项式一定有常数项。）

生成校验码
为了确保附加了校验码的二进制数能够被多项式对应的二进制数整除，需要通过如下的步骤来生成校验码：

1. 在原始数据后面补 0，0 的个数和多项式的最高次数相同
2. 补 0 后的二进制数与多项式的二进制数进行模 2 除法，得到余数，余数即为校验码。（余数的位数和多项式的最高次数相同）

   模 2 运算：加法不进位，减法不借位，也就是异或运算

海明纠错码

整体过程
在数据位中划分出多个奇偶校验组，每组使用一位校验位来校验；
一个数据位同时存在于多个校验组中，接受多个校验位的校验；
发送方根据奇偶校验组计算出校验位，插入到发送的信息中。
接收方收到后，对每个奇偶校验组做校验，根据得到的结果来判断是否出错，以及哪一位出错了。

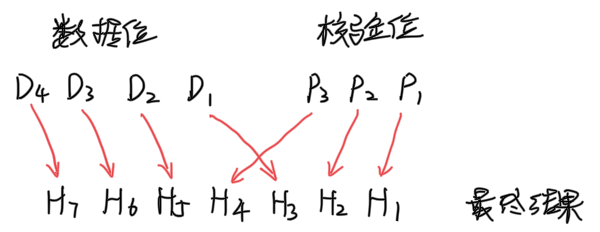
校验位的位置
校验位被插入到数据位中，第 位校验位应该位于最终结果的第 位，数据位按照顺序插入到剩下的位置：

划分奇偶校验组
每个数据位同时存在于多个校验组中，接受多个校验位的校验，这些校验位的海明位号之和等于这个数据位的海明位号。由同一个校验位来校验的数据位组成了一个奇偶校验组。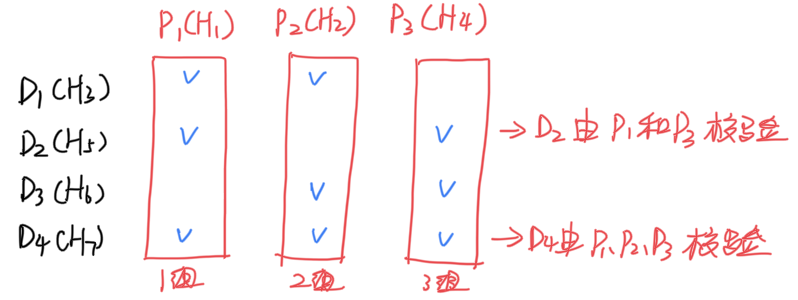

计算校验位
一个奇偶校验组对应一个校验位，校验组中的所有数据位进行异或运算，得到校验位：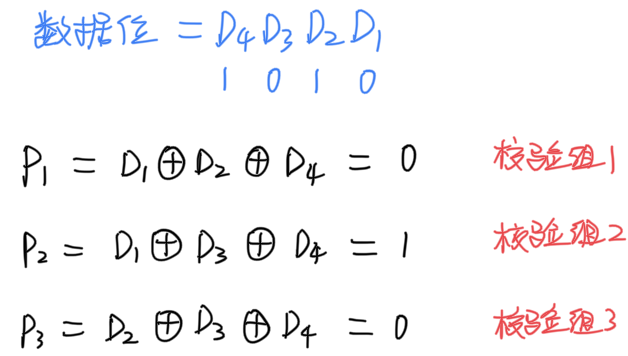

进行纠错
接收方收到后，分别对每个校验组以及校验位进行异或运算，得到的结果组成二进制数。如果结果为 0，表示没有出错；否则，结果就表示出错的数据位数

海明码的纠错能力
如果要对一位数据位进行纠错，则数据位和校验位的位数需要满足以下关系：
设数据位的位数为 ，校验位的位数为 ，则有：