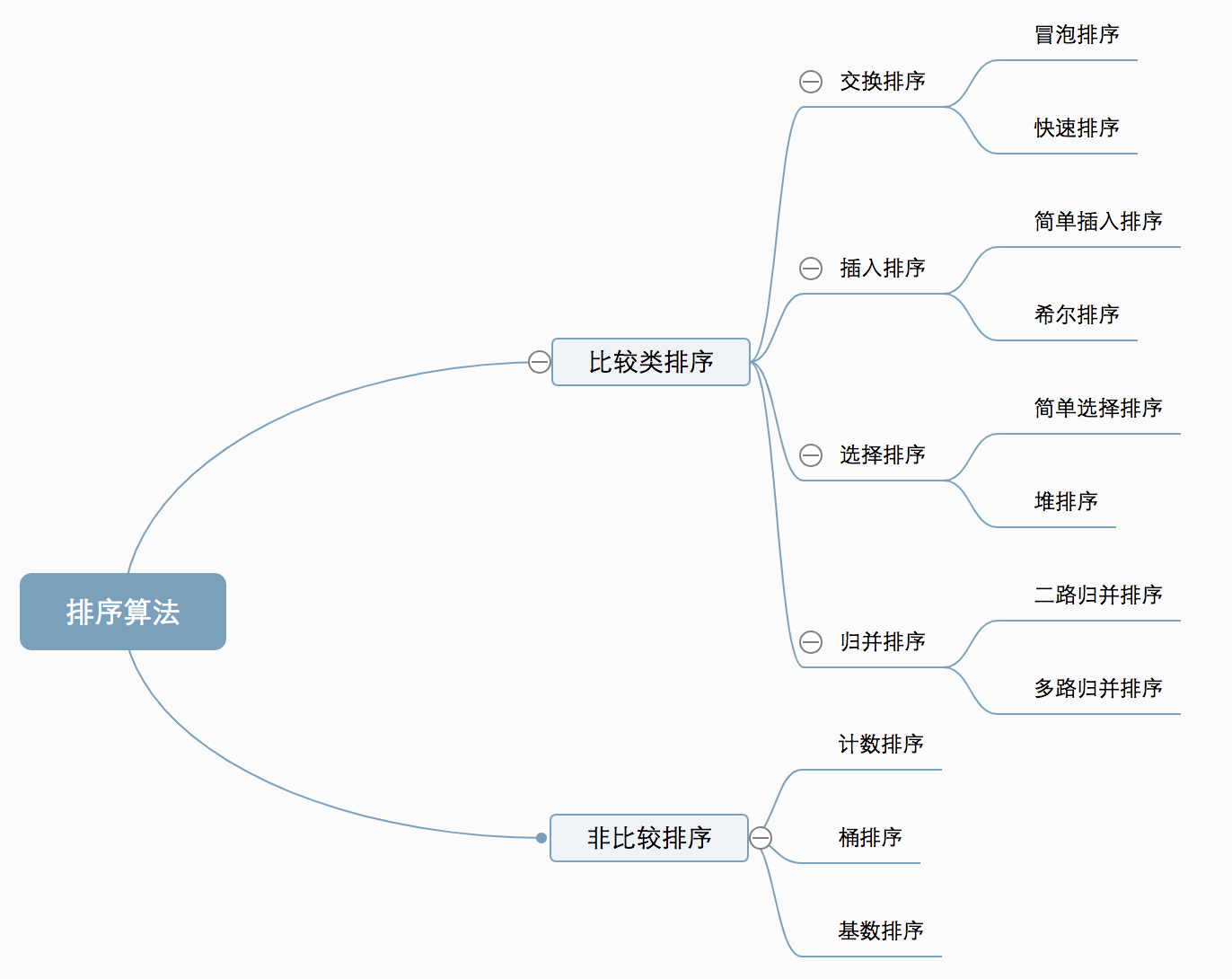
排序算法1.png
排序算法.png

冒泡排序

  1. for(int i = 0 ;i<arr.length-1;i++){
  2.         //第i趟比较
  3.         for(int j = 0 ;j<arr.length-i-1;j++){
  4.             //开始进行比较，如果arr[j]比arr[j+1]的值大，那就交换位置
  5.             if(arr[j]>arr[j+1]){
  6.                 int temp=arr[j];
  7.                 arr[j]=arr[j+1];
  8.                 arr[j+1]=temp;
  9.             }
  10.         }
  11.     }

选择排序

  1. for(int i=0;i<nums.length-1;i++){
  2.     for(int j=i+1;j<nums.length;j++){
  3.         if(nums[i]>nums[j]){
  4.             int temp = nums[j];
  5.             nums[j] = nums[i];
  6.             nums[i]=temp;
  7.         }
  8.     }
  9. }

快速排序

选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分；其中一部分的所有数据都比另外一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

  1. public static void quickSort(int[] nums ,int low,int high){
  2.     if(low<high){
  3.         int getIndex = getIndex(nums,low,high);
  4.         quickSort(nums,low,getIndex-1);
  5.         quickSort(nums,getIndex+1,high);
  6.     }
  7. }
  8. public static int getIndex(int[] nums, int low, int high){
  9.     int temp = nums[low];
  10.     while(low<high){
  11.         if(low<high && nums[high]>=temp){
  12.             high --;
  13.         }
  14.         nums[low] = nums[high];
  15.         if(low<high && nums[low]<=temp){
  16.             low ++;
  17.         }
  18.         nums[high] = nums[low];
  19.     }
  20.     nums[low] = temp;
  21.     return low;
  22. }

二分查找（O（ log2n ））

int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) { // 注意
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
        }
    return -1;
}

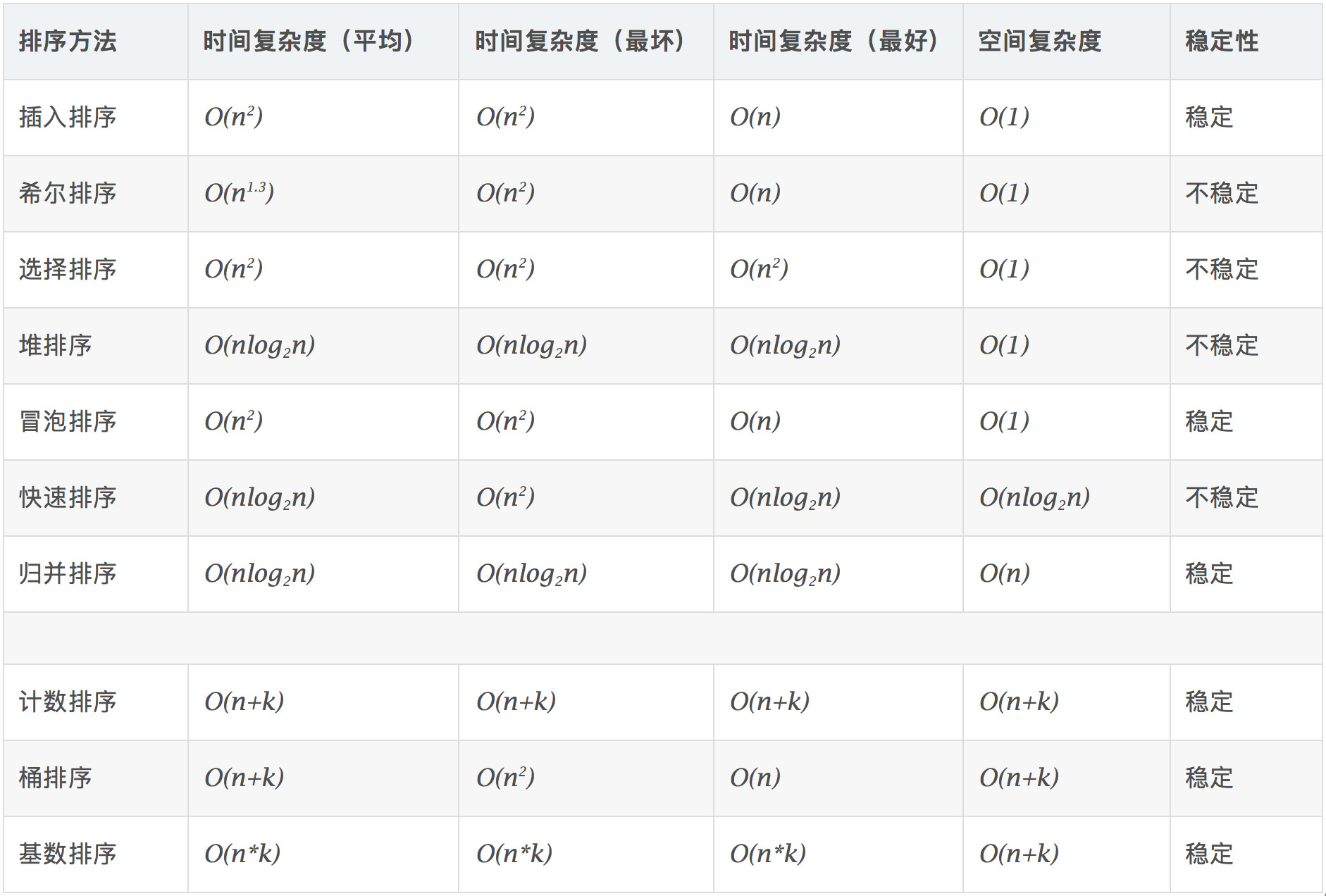
时间复杂度与空间复杂度

衡量代码的好坏包括两个非常重要的指标：
1.运行时间
2.占用空间

  • 时间维度：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述。

  • 空间维度：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述。

    时间复杂度

    时间频度 一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。
    并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
    时间复杂度 在刚才提到的时间频度中，n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此，我们引入时间复杂度概念。 一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

    参考资料

  • 漫画:什么是时间复杂度?

  • 十大经典排序算法（动图演示）
  • 归并排序