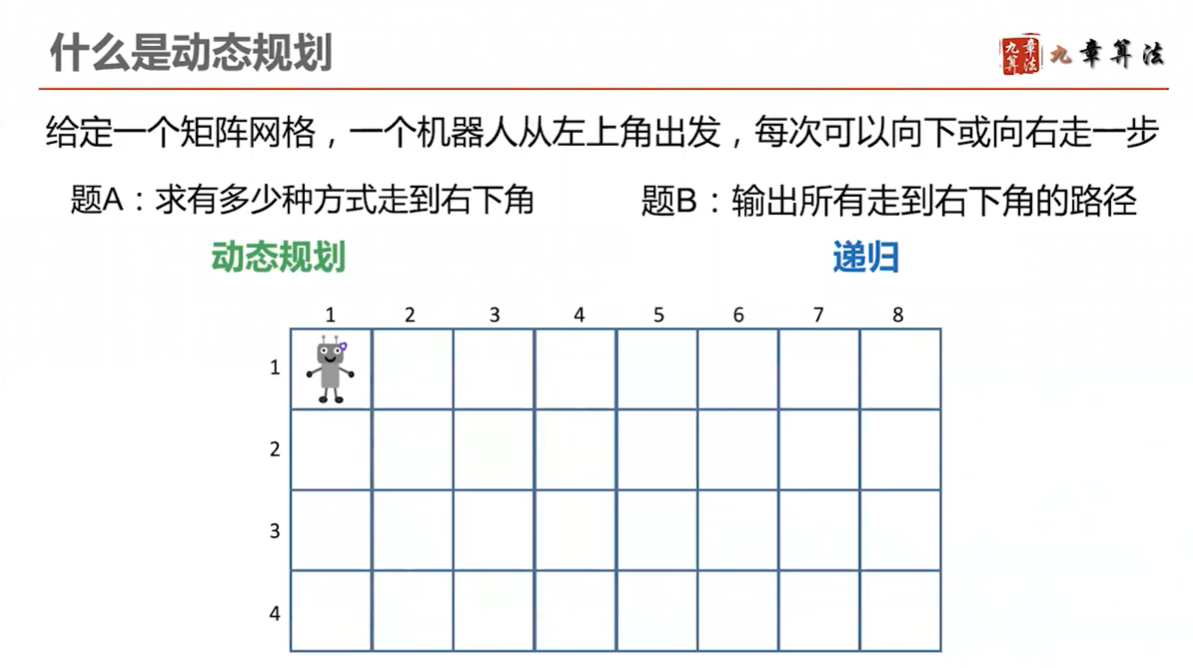
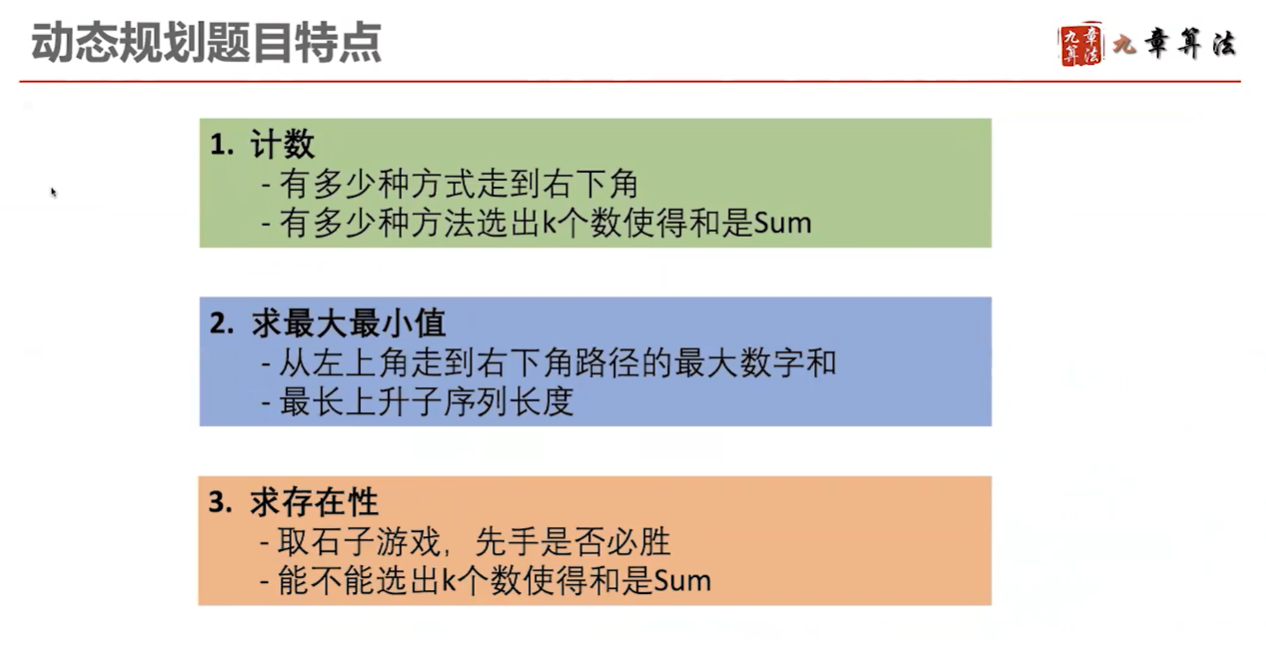
image.png
image.png

  • 问题可以采用递归的方法进行解决
  • 递归方法存在着重复计算的问题
  • 采用动态规划的方式解决，将重复的计算记录下来

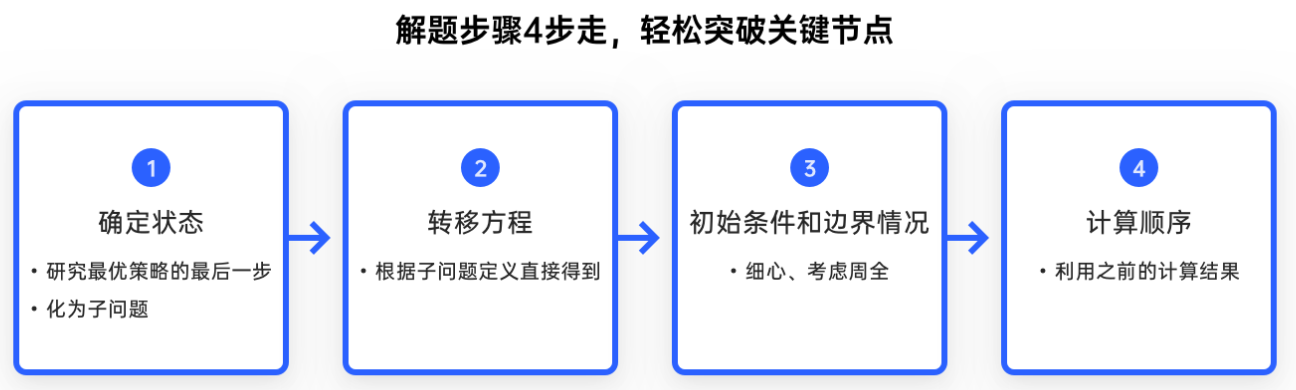
image.png

1.dp数组的定义和下标。
2.递推公式。
3.dp数组如何初始化，初始化也需要注意。
4.遍历顺序，比较考究，01 先遍历背包，后遍历物品。
4.1排列和组合的遍历顺序是不相同的。
4.1.1 排列：背包在外 物品在内。（322）
4.1.2 组合：物品在外，背包在内。（518）
5.（出现问题）打印dp数组。（打印dp数组，检查是否有问题，检验1 2 3 4 步骤）

举个栗子

Leetcode.70.爬楼梯

  1.     // 70. 爬楼梯
  2.     /**
  3.      * f(10) = f(9)+f(8)
  4.      * f(9) = f(8) + f(7)
  5.      * ......
  6.      * f(3) = f(2) + f(1)
  7.      * f(2) = f(1)+1
  8.      * f(1) = 1
  9.      */
  12.     // 递归解法  能运行到45
  13.     public static int climbStairs1(int n) {
  14.         if(n == 2){
  15.             return 2;
  16.         }
  17.         if(n == 1){
  18.             return 1;
  19.         }
  20.         return climbStairs1(n-1)+climbStairs1(n-2);
  21.     }
  24.     //动态规划解法
  25.     // 使用累加的方式，将上一个值记住
  26.     // 重复的值不需要重复的相加
  27.     public static int climbStairs2(int n) {
  28.         if(n == 2){
  29.             return 2;
  30.         }
  31.         if(n == 1){
  32.             return 1;
  33.         }
  35.         int count = 0;
  36.         int a = 1;
  37.         int b = 2;
  38.         for(int i = 3;i<=n;i++){
  39.             count = a+b;  //累加结果  契合总结的公式  下一个总数是前两个相加
  40.             //向下迭代
  41.             a = b;  //a成为上上个台阶 下次迭代的第n-2个台阶的走法等于上次迭代n-1个台阶的走法
  42.             b = count; //b成为上一个台阶 下次迭代的第n-1个台阶的走法等于上次迭代的第n个台阶走法
  43.         }
  44.         return count;
  46.     }

示例

题：509. 斐波那契数(注意边界问题)

  1. public int fib(int n) {
  2.         if(n == 0){return 0; }
  3.         if(n == 1){ return 1; }
  4.         int[] dp = new int[n+1];
  5.         dp[0] = 0;
  6.         dp[1] = 1;
  8.         // 注意边界问题，是 i<=n 还是 i<n
  9.         for(int i=2;i<=n;i++){
  10.             dp[i] = dp[i-1] + dp[i-2];
  11.         }
  13.         return dp[n];
  14.     }

题：5. 最长回文子串

  1. //双层循环
  2. public String longestPalindrome(String s) {
  3.         String res = s.substring(0,1);
  4.         int n = s.length();
  5.         boolean[][] dp = new boolean[n][n];
  7.         for(int i=n-1;i>=0;i--){
  8.             for(int j=i;j<n;j++){
  9.                 // 开头等于末尾并且（三个字符或者开头与结尾之间的字符串（正下方）是回文）
  10.                 if(s.charAt(i) == s.charAt(j) &&(j-i<=2 || dp[i+1][j-1])){
  11.                     dp[i][j] = true;
  12.                     res = s.substring(i,j+1).length()>res.length()?s.substring(i,j+1):res;
  13.                 }
  14.             }
  15.         }
  17.         return res;
  18.     }

f5801ed7716d857d85029a059bce6f5.jpg

循序渐进

  • 爬楼梯
  • 背包问题
  • 打家劫舍
  • 股票问题
  • 子序列问题
  • 边距距离问题

    01背包问题

    01背包问题的模版 ```java //01背包 for (int i = 0; i < n; i++) { for (int j = m; j >= V[i]; j—) {
    1.   f[j] = max(f[j], f[j-V[i]] + W[i]);
    } } //完全背包 for (int i = 0; i < n; i++) { for (int j = V[i]; j <= m; j++) {
      f[j] = max(f[j], f[j-V[i]] + W[i]);
    } }

/ f[j]代表当前背包容量为j的时候，可以获取的最大价值。 完全背包是从左向右遍历，f[j-V[i]]取到的是拿第i个物品时的值，是新值， 可以重复无限的拿，f[j]的值也会随之增加。 V：商品的体积 W：商品的价值 /

<a name="Civ7M"></a>
### No经典01背包问题
```java
public class No经典01背包问题 {
    /**
     * 问题描述：
     * 现有4个物品，小偷背包的容量为8，怎么样能偷到价值最多的东西？
     * 如：
     * 物品表号： 1  2  3  4
     * 物品重量： 2  3  4  5
     * 物品价值： 3  4  5  8
     */
    public static void main(String[] args) {
        int[] nums1 = {2,3,4,5};
        int[] nums2 = {3,4,5,8};
        System.out.println(rob(nums1,nums2,8));
    }

    /**
     * 1. 动态规划  01背包问题
     * 画表格可以辅助理解
     * @param nums1
     * @param nums2
     * @param sum
     * @return
     */
    public static int rob(int[] nums1, int[] nums2, int sum){
        int len1 = nums1.length;
        int[][] dp = new int[len1][sum+1];  //价值
        for(int i=0;i<len1;i++){
            for(int j=0;j<=sum;j++){
                if(nums1[i] > j){
                    if(i==0){  //初始化边界
                        dp[i][j] = 0;
                    }else{
                        dp[i][j] = dp[i-1][j];
                    }
                }else {
                    if(i==0){  //初始化边界
                        dp[i][j] = nums2[i];
                    }else {
                        dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-nums1[i]]+nums2[i]);
                    }

                }
            }
        }
        return dp[len1-1][sum];
    }

    /**
     * 2. 暴力解法  使用回溯遍历  时间复杂度为 2的n次方
     */
}

416. 分割等和子集

public static boolean canPartition(int[] nums) {
        int sum = 0;
        for (int n : nums) {
            sum += n;
        }
        if(sum % 2 != 0) return false;//整数相加不可能得小数
        int W = sum / 2;//相当于背包总承重
        int [] dp = new int[W+1];  //dp[i]  表示实现i 的情况有几种，w+1 是为了与w和数组下标对应
        dp[0] = 1;  //实现0 的情况有一种
        for (int num : nums) {
            for (int i = W; i >= num; i--) {
                dp[i] += dp[i-num];
            }
        }
        return dp[W] != 0;
    }

参考资料