机器学习模型

机器学习，从其名称上来看，是期望机器能够像人一样学习，甚至于超过人类.
理想是丰满的，现实是骨感的, 现阶段的机器学习依旧是按照预定义的程序的进行执行. 那么机器学习算法和传统的算法有什么区别呢。 假设一个控制交通灯的程序, 它能根据新的输入来改变其行为去适应新的情况. 这种貌似没有认为干预而产生的适应性, 便让人以为机器学会自己学习了. 然而，在机器学习模型的表象之下, 这种适应行为其实是在人类的设计下严格执行的机器指令。

那么什么是机器学习模型?

机器学习算法是揭示数据中潜在关系的过程。 机器学习模型（machine learning model）是机器学习算法产出的结果，可以将其看作是在给定输入情况下、输出一定结果的函数（function） \mathtt{F}F。 机器学习模型不是预先定义好的固定函数，而是从历史数据中推导出来的。因此，当输入不同的数据时，机器学习算法的输出会发生变化，即机器学习模型发生改变。

例如，在图像识别的场景中，可以训练机器学习模型来识别照片中的对象。在某种情况下，人们可能会将数千张有猫和没有猫的图像输入到机器学习算法中，以获得一个能够判断照片中是否有猫的模型。因此，生成的模型对应的输入将是一张数字照片，而输出是一个表示照片上是否存在猫的布尔值。

在上述情况下，机器学习模型是一个将多维像素值映射到二进制值的函数。假设我们有一张 3 维像素的照片，每个像素的值范围从 0 到 255。那么输入和输出之间的映射空间将是 (256 \times 256 \times 256) \times 2(256×256×256)×2，大约是 3300 万。我们可以说服自己，在现实世界的案例中学习这种映射（机器学习模型）一定是一项艰巨的任务，因为在这种情况下，一张普通照片占到数百万像素，并且每个像素由三种颜色（RGB）组成，而不是单一的灰色。

机器学习的任务，就是从广阔的映射空间中学习函数。

在这种情况下，找出数百万像素和 “是/否” 答案之间的潜在映射关系的过程，就是我们所说的机器学习。大多数时候，我们学习的最后结果是对这种潜在关系的一种近似。由于机器学习模型的近似性质，人们不应该因发现机器学习模型的结果往往无法达到 100 \%100% 精确而感到失望。在 2012 年深度学习被广泛应用之前，最好的机器学习模型只能在 ImageNet 视觉识别挑战 中达到 75 \%75% 精度。到目前为止，还没有一种机器学习模型能够保证 100 \%100% 精确，尽管在这项任务中，有一些模型的误差要比人类少 \lt 5 \%<5%。

有监督和无监督

给出一个机器学习问题，首先可以确定它是有监督（supervised） 问题还是无监督（unsupervised） 问题。
对于任何机器学习问题，我们都从一组样本（samples）组成的数据集开始。每个样本可以表示为一个属性（attributes）元组。
例如，有一个名为 Iris 的著名经典数据集，首次发表于 Ronald. A. Fisher 在 1936 年的论文 “The use of multiple measurements in taxonomic problems（可译作：多重测量在分类学问题中的使用）”。Iris 数据集包括对 150 个鸢尾花样本的测量。每个样本都包含其花瓣和萼片的长度和宽度的测量值，以及指示鸢尾花类别的属性，即山鸢尾、变色鸢尾和维吉尼亚鸢尾。以下是 Iris 数据集的一些示例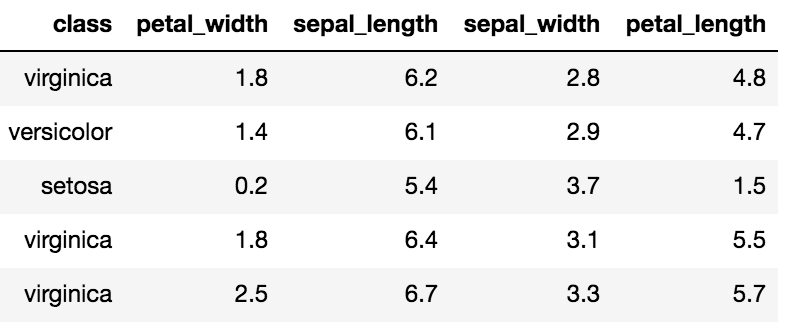

有监督学习

在一个有监督的学习任务中，数据样本将包含一个目标属性 yy，也就是所谓的真值（ground truth）。我们的任务是通过学习得到一个函数 F，它接受非目标属性 X，并输出一个接近目标属性的值，即 F(X) \approx yF(X)≈y。目标属性 yy 就像指导学习任务的教师，因为它提供了一个关于学习结果的基准。所以，这项任务被称为有监督学习。
在 Iris 数据集中，类别属性（鸢尾花的类别）可以作为目标属性。具有目标属性的数据通常称为 “标记” 数据（labeled data）。基于上述定义，，可以看出用标记数据预测鸢尾花的种类的任务是一个有监督的学习任务。

无监督学习

与有监督的学习任务相反，我们在无监督的学习任务中没有设置真值。人们期望从数据中学习潜在的模式或规则，而不以预先定义的真值作为基准。
人们可能会问，如果没有来自真值的监督，我们还能学到什么吗？答案是肯定的。以下是一些无监督学习任务的示例：

• 聚类（Clustering）：给定一个数据集，可以根据数据集中样本之间的相似性，将样本聚集成组。例如，样本可以是一个客户档案，具有诸如客户购买的商品数量、客户在购物网站上花费的时间等属性。根据这些属性的相似性，可以将客户档案分组。对于聚集的群体，可以针对每个群体设计特定的商业活动，这可能有助于吸引和留住客户。
• 关联（Association）：给定一个数据集，关联任务是发现样本属性之间隐藏的关联模式。例如，样本可以是客户的购物车，其中样本的每个属性都是商品。通过查看购物车，人们可能会发现，买啤酒的顾客通常也会买尿布，也就是说，购物车里的啤酒和尿布之间有很强的联系。有了这种学习而来的洞察力，超市可以将那些紧密相关的商品重新排列到相邻近的角落，以促进这一种或那一种商品的销售。

  半监督学习

  在数据集很大，但标记样本很少的情况下，可以找到同时具备有监督和无监督学习的应用。我们可以将这样的任务称为半监督学习（semi-supervised learning**）**。
  在许多情况下，收集大量标记的数据是非常耗时和昂贵的，这通常需要人工进行操作。斯坦福大学的一个研究团队花了两年半的时间来策划著名的 “ImageNet”，它包含了数以百万计的图像带有成千上万个手动标记的类别。因此，更普遍的情况是，我们有大量的数据，但只有很少一部分被准确地 “标记”，例如视频可能没有类别甚至标题。

  通过将有监督和无监督的学习结合在一个只有少量标记的数据集中，人们可以更好地利用数据集，并获得比单独应用它们更好的结果。

例如，人们想要预测图像的分类，但只对图像的 10 \%10% 进行了标记。通过有监督的学习，我们用有标记的数据训练一个模型，然后用该模型来预测未标记的数据，但是我们很难相信这个模型是足够普遍的，毕竟我们只用少量的数据就完成了学习。一种更好的策略是首先将图像聚类成组（无监督学习），然后对每个组分别应用有监督的学习算法。第一阶段的无监督学习可以帮助我们缩小学习的范围，第二阶段的有监督学习可以获得更好的精度。

分类和回归

在前一节中，我们将机器学习模型定义为一个函数 FF，它接受一定的输入并生成一个输出。通常我们会根据输出值的类型将机器学习模型进一步划分为分类（classification）和回归（regression）。

如果机器学习模型的输出是离散值（discrete values），例如布尔值，那么我们将其称为分类模型。如果输出是连续值（continuous values），那么我们将其称为回归模型。

分类模型

例如，说明照片中是否包含猫的模型可以被视为分类模型，因为我们可以用布尔值表示输出。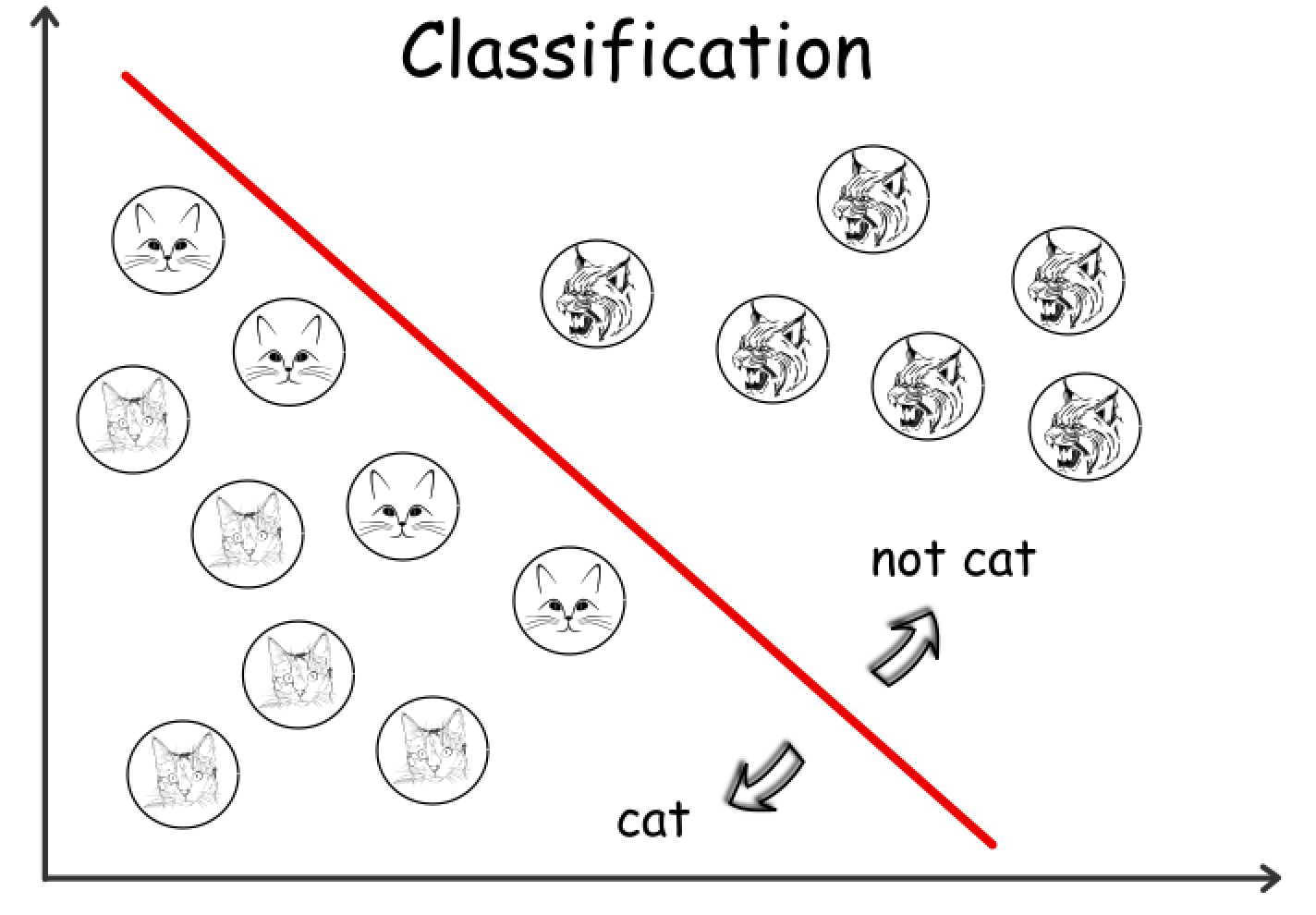

更具体地说，输入可以表示为矩阵 MM，尺寸为 H \times WH×W，其中 HH 是照片的高度（像素），WW 是照片的宽度。矩阵中的每个元素都是照片中每个像素的灰度值，即一个介于 [0, 255][0,255] 之间的整数，表示颜色的强度。模型的预期输出为二进制值 [1|0][1∣0]，用于指示照片是否显示猫。综上所述，我们的猫照片识别模型 FF 可表述如下：
F(M[H][W]) = 1 | 0, \text{where} \space M[i][j] \in [0, 255], 0 \lt i \lt H, 0 \lt j \lt WF(M[H][W])=1∣0,where M[i][j]∈[0,255],0<_i_<_H_,0<_j_<_W_
机器学习的目标是找出一个尽可能通用的函数，这个函数要尽可能对不可见数据给出正确的答案。

回归模型

对于回归模型，我们给出这样一个例子，考虑一个用于估算房产价格的模型，其特征包括诸如面积、房产类型（例如住宅、公寓），当然还有地理位置。在这种情况下，我们可以将预期输出看作是一个实数 p \in {\mathbb R}p∈R，因此它是一个回归模型。注意，在本例中，我们所拥有的原始数据并非全部是数字，其中某些数据是用于分类的，例如房地产类型。在现实世界中，情况往往就是这样的。
对于每个正在考虑的房产，我们可以将其特征用元组 TT 来表示，其中元组中的每个元素要么是数值，要么是表示其属性之一的分类值。在许多情况下，这些元素也被称为 “特征（features）”。综上所述，我们可以建立如下的房产价格估算模型：
F(T) = p, \text{where} \space p \in \mathbb{R}F(T)=p,where p∈R
再具体一些，让我们考虑一个具有以下特征的房产：
surface = 120 \space m^2120 m_2, type = ‘ apartment’, location = ‘ NY downtown’, year_of_construction = 2000
现在考虑到上述特征，如果我们的模型 F_F 给出了一个像 {10,000\$}10,000$ 这样的值，那么很可能我们的模型并不适合这个问题。
在下面的图表中，我们展示了一个以地产面积为唯一变量，以地产价格为输出的回归模型样例。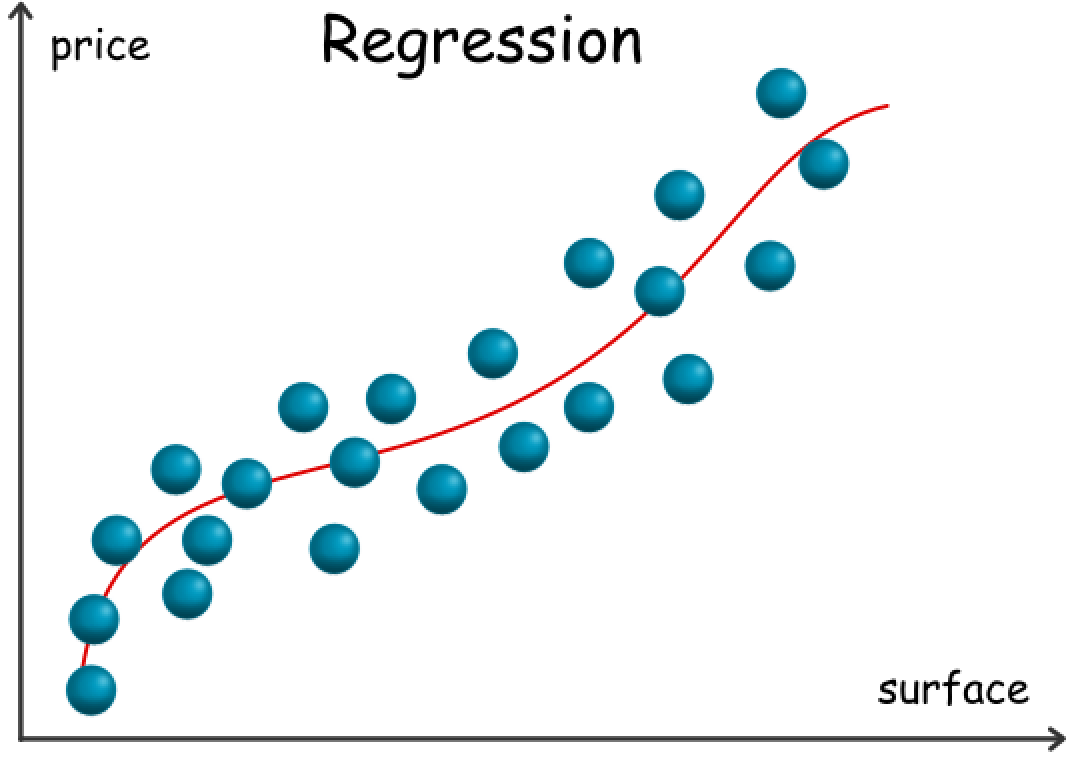

说起特征，还要提到的一点是，一些机器学习模型（例如决策树）可以直接处理非数字特征，而更多时候人们必须以某种方式将这些非数字特征转换（transform）为数字特征。

问题转化

对于一个现实世界的问题，有时人们可以很容易地将其表述出来，并快速地将其归结为一个分类问题或回归问题。然而，有时这两个模型之间的边界并不清晰，人们可以将分类问题转化为回归问题，反之亦然。
在上述房产价格估算的例子中，似乎很难预测房产的确切价格。然而，如果我们将问题重新表述为预测房产的价格范围，而不是单一的价格标签，那么我们可以期望获得一个更健壮的模型。因此，我们应该将问题转化为分类问题，而不是回归问题。
对于我们的猫照片识别模型，我们也可以将其从分类问题转换为回归问题。我们可以定义一个模型来给出一个介于 [0, 100\%][0,100%] 之间概率值来判断照片中是否有猫，而不是给出一个二进制值作为输出。这样，就可以比较两个模型之间的细微差别，并进一步调整模型。例如，对于有猫的照片，模型 A 给出概率为 1 \%1%，而模型 B 对相同照片给出了 49 \%49% 的概率。虽然这两种模型都没有给出正确的答案，但我们可以看出，模型 B 更接近于事实。在这种情况下，人们经常应用一种称为逻辑回归（Logistic Regression）的机器学习模型，这种模型将连续概率值作为输出，但用于解决分类问题。

参考资料:
https://leetcode-cn.com/explore/featured/card/machine-learning-101/253/machine-learning-what/1093/