笔者今天在做力扣每日一题时，遇到一道经典的BFS题目：

面试题13. 机器人的运动范围

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1： 输入：m = 2, n = 3, k = 1

输出：3

示例 1：

输入：m = 3, n = 1, k = 0

输出：1

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

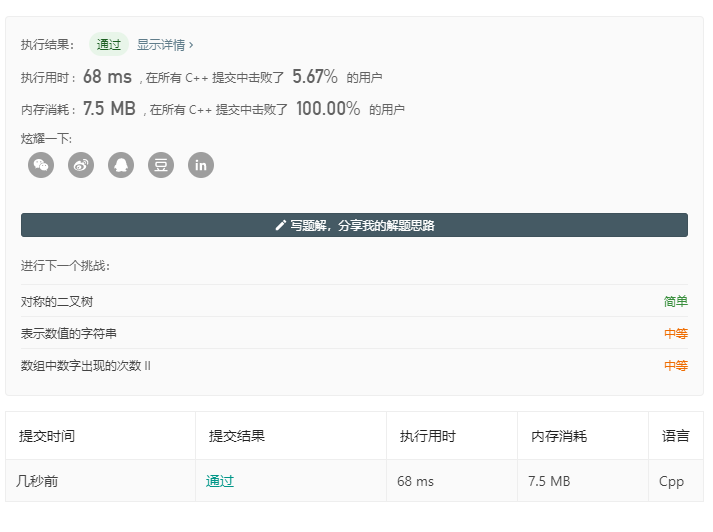
采用BFS的方法可以很轻松的解决这道题。这里我采用的C++来实现的BFS，在用C++实现BFS时，需要注意的是两个关键的数据结构，一个是队列，用以实现广度搜索，一个是map，用以判断已经“走”过的节点。同时这道题中，还应用了一个map用以计算已经计算过的值，是典型的空间换时间的思路（不过比较搞笑的是，最终结果显示的是空间击败了100%，但时间只击败了5.67%）。

image.png
以下是我的代码，还有优化的空间，但这个代码却是可以很好的反映出BFS的思路

  1. class Solution {
  2. public:
  3.     map<int, int>valuestore;
  5.     int getvalue(int x)
  6.     {
  7.         if (x >= 0 && x <= 9)
  8.             return x;
  10.         if (valuestore.find(x) != valuestore.end())
  11.             return valuestore[x];
  13.         int ret = 0;
  15.         while (x)
  16.         {
  17.             ret += x % 10;
  18.             x = x / 10;
  19.         }
  21.         valuestore[x] = ret;
  23.         return ret;
  24.     }
  27.     int movingCount(int m, int n, int k) {
  28.         if (k == 0)
  29.         return 1;
  31.         queue<pair<int, int>>bfs;
  32.         map<pair<int, int>, int>store;
  34.         bfs.push(pair<int, int>{0, 0});
  36.         int step = 0;
  38.         while (!bfs.empty())
  39.         {
  40.             pair<int, int>tmp = bfs.front();
  41.             bfs.pop();
  42.             store[tmp] = 1;
  44.             step++;
  46.             int x = getvalue(tmp.first);
  47.             int y = getvalue(tmp.second);
  49.             if (tmp.first + 1 < m && (getvalue(tmp.first + 1) + y <= k))
  50.             {
  51.                 pair<int, int>move{ tmp.first + 1, tmp.second };
  52.                 if (store[move] != 1)
  53.                 {
  54.                     bfs.push(move);
  55.                     store[move] = 1;
  56.                 }
  57.             }
  59.             if (tmp.first - 1 >= 0 && (getvalue(tmp.first - 1) + y <= k))
  60.             {
  61.                 pair<int, int>move{ tmp.first - 1, tmp.second };
  62.                 if (store[move] != 1)
  63.                 {
  64.                     bfs.push(move);
  65.                     store[move] = 1;
  66.                 }
  67.             }
  69.             if (tmp.second + 1 < n && (x + getvalue(tmp.second + 1) <= k))
  70.             {
  71.                 pair<int, int>move{ tmp.first, tmp.second + 1 };
  72.                 if (store[move] != 1)
  73.                 {
  74.                     bfs.push(move);
  75.                     store[move] = 1;
  76.                 }
  77.             }
  79.             if (tmp.second - 1 >= 0 && (x + getvalue(tmp.second - 1) <= k))
  80.             {
  81.                 pair<int, int>move{ tmp.first, tmp.second - 1 };
  82.                 if (store[move] != 1)
  83.                 {
  84.                     bfs.push(move);
  85.                     store[move] = 1;
  86.                 }
  87.             }
  88.         }
  90.         return step;
  91.     }
  92. };