8.1 基本思想
动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，由于分治法采用自上而下的方式求值，有些子问题被重复计算了很多次；在动态规划中采用自下向上求值，并把中间结果存储起来，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。
斐波那契数列： f(n)=f(n-1)+f(n-2)
=[f(n-2)+f(n-3)]+[f(n-3)+f(n-4)]
={[f(n-3)+f(n-4)]+[f(n-4)+f(n-5)]} +{[f(n-4)+f(n-5)]+[f(n-5)+f(n-6)]}
8.2 剪绳子
8.2.1 题目
给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。
输入：10 输出：36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
8.2.2 递推过程
在长度为 n 的绳子上任意剪一段 i ，那么乘积就是前开后两段绳子最大乘积（与原问题一致）的乘积，为保存乘积最大，则最大乘积 f(n) = max(f(i) * f(n-i)) 1 < i < n 。
直接采用递归进行自上向下求值会遇到大量重复子问题。
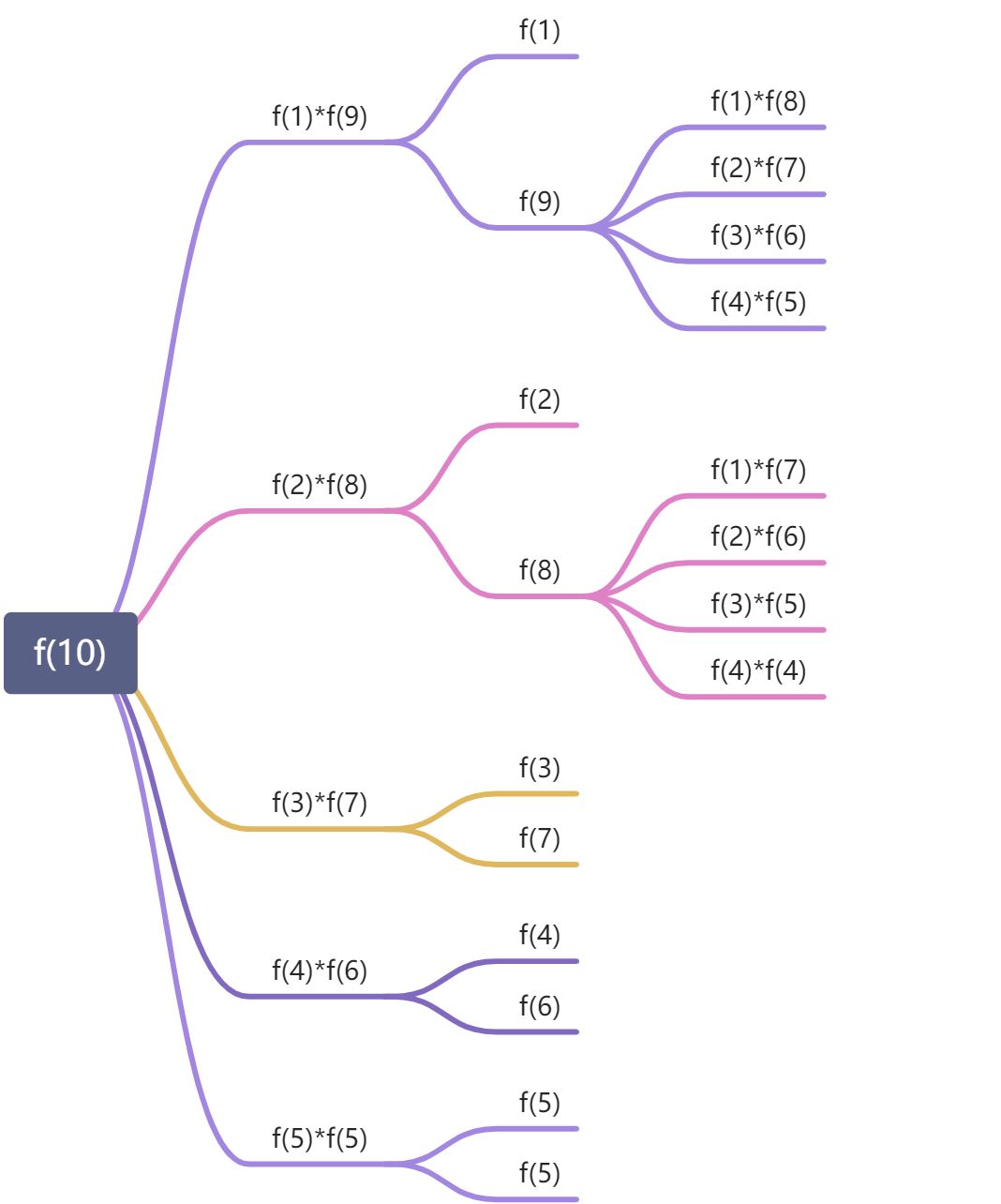采用动态规划自下向上求值，将已计算的值记录到表中，避免重复求值。
| 循环 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | f(1) | f(2) | f(3) | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 1 | f(1) | f(2) | f(3) | f(4) | -1 | -1 | -1 | -1 | -1 | -1 |
| 2 | f(1) | f(2) | f(3) | f(4) | f(5) | -1 | -1 | -1 | -1 | -1 |
| 3 | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | -1 | -1 | -1 | -1 |
| 4 | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | -1 | -1 | -1 |
| 5 | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | -1 | -1 |
| 6 | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | f(9) | -1 |
| 7 | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | f(9) | f(10) |
8.3 把数字翻译成字符串
8.3.1 题目
给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。
输入：12258 输出：5 解释: 12258有5种不同的翻译，分别是”bccfi”, “bwfi”, “bczi”, “mcfi”和”mzi”
8.3.2 递推过程
对于长度为n的字符串，从尾部开始看：
- 把最后个一个数字单独翻译成字符，相当于在长度为n-1的字符串的翻译结果后添加一个字符，所以产生的翻译方法数就是长度为n-1的字符串翻译方法总数（与原问题一致）；
- 把最后两个数字一起翻译成字符（最后两个数字可以一起翻译），相当于在长度为n-2的字符串的翻译结果后添加一个字符，所以产生翻译方法数就是长度为n-2的字符串翻译方法总数（与原问题一致）；
所以，翻译方法总数为这两种情况之和，即dp(n) = dp(n-1) + dp(n-2)。完整的递推公式如下：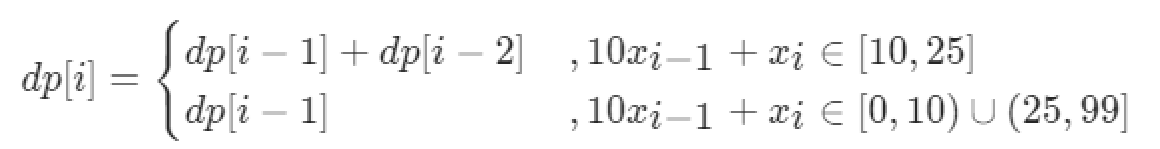
采用递归计算的过程如下：
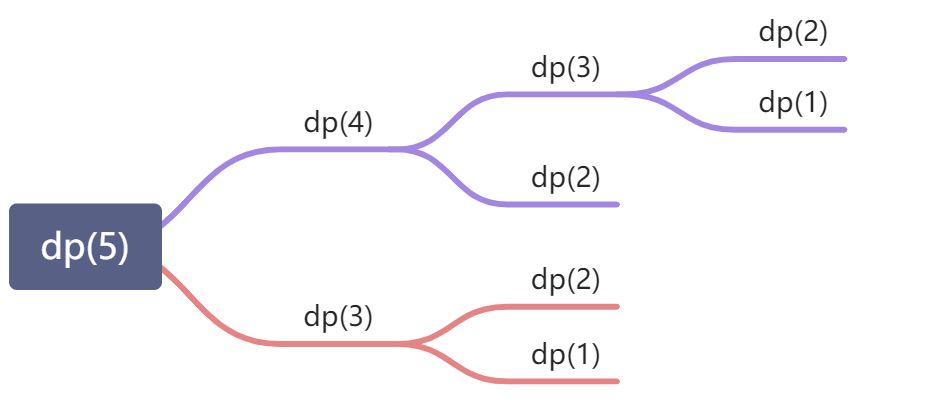采用动态规划，自下而上求值：12258
| 循环 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0 | 1(b) | 2(bc / m) | -1 | -1 | -1 |
| 1 | 1 | 2 | 3(bcc, mc / bw) | -1 | -1 |
| 2 | 1 | 2 | 3 | 5(bccf, mcf, bwf / bcz, mz) | -1 |
| 3 | 1 | 2 | 3 | 5 | 5(bccfi, mcfi, bwfi, bczi, mzi) |
8.4 最长不含重复字符的字符串
8.4.1 题目
请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。
输入: “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是”abc”，所以其长度为 3。
输入: “bbbbb” 输出: 1 解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
输入: “pwwkew” 输出: 3 解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。 请注意，你的答案必须是 子串 的长度，”pwke” 是一个子序列，不是子串。
8.4.2 递推过程
对于长度为n的字符串，从尾部开始看，计算该最长子字符串的长度可以先计算长度n-1字符串的字符串长度，然后与以第n个字符中结尾的最长子字符串相比。那么本题就变为从尾部开始，查找最早出现重复字符位置的问题了。
对于abcabcbb而言，abcabcb的子串应是abc，以最后一个字符结尾的子串是b，所以最终长度为3
此时可以建立递推公式：· f(n) = max(f(n-1), x) 。
但是对于abcdefjhijklmnopqrstuvwxyzabcdefjhijklmnopqrstuvwxyz 这种字符串来说，查找结尾子串会反复遍历同一块区域。为了减少重复遍历，需要采取以下两个措施：
- 记录以
n-1结尾的最长子串长度dp(n-1)。在以n-1结尾的子串长度内没有出现第n个字符，那么dp(n) = dp(n-1)+1，如果出现了，那么dp(n) = n - x，显然此时依然要重复遍历，只是不需要查重的额外空间了； - 记录字符最新的位置。在自下向上的递推过程中，不断更新字符出现的位置，需要时可以直接读取到第n个字符出现的下标，以此来判断第n个字符是否在以n-1字符结尾的子串中。
改进后的动态规划递推公式为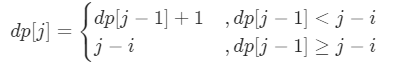
对于abcabcbb而言
| 0 | 1 | 2 | 3 | 4 | 5 | …… | 8 | |
|---|---|---|---|---|---|---|---|---|
| dp | [] | [1] | [1, 2] | [1, 2, 3] | [1, 2, 3, 3] | [1, 2, 3, 3, 3] | …… | [1, 2, 3, 3, 3, 2, 1] |
| dic | {} | {a:0} | {a:0, b:1} | {a:0, b:1, c:2} | {a:3, b:1, c:2} | {a:3, b:4, c:2} | …… | {a:3, b:7, c:5} |
| tmp | 0 | 1 | 1+1 | 2+1 | 3-0 | 4-1 | …… | 7-6 |
| max | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 3 |
8.5 礼物的最大价值
8.5.1 题目
在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？
输入: [ [1,3,1], [1,5,1], [4,2,1] ] 输出: 12 解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
8.5.2 递推过程
起点为左上角，终点为右下角，从终点反向看，设到达终点所获得的值为 f(m, n) ，由于每次只有向右或者向下移动，所以一个点只能由它的上面和左边进入，那么终点的值可表达为 f(m, n) = max(f(m-1, n), f(m, n-1))+value(m, n)，为此需要求解 f(m-1, n) 和 f(m, n-1) ，也就是当棋盘为 m-1*n 和 m*n-1 大小时礼物最大价值。
采用递归的思想依然会遇到重复子问题。
采用动态规划的过程如下：
| 1 | 3 | 1 |
|---|---|---|
| 1 | 5 | 1 |
| 4 | 2 | 1 |
| 1 | 4 | 1 |
|---|---|---|
| 1 | 5 | 1 |
| 4 | 2 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 1 | 5 | 1 |
| 4 | 2 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 2 | 5 | 1 |
| 4 | 2 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 2 | 9 | 1 |
| 4 | 2 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 2 | 9 | 10 |
| 4 | 2 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 2 | 9 | 10 |
| 6 | 2 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 2 | 9 | 10 |
| 6 | 11 | 1 |
| 1 | 4 | 5 |
|---|---|---|
| 2 | 9 | 10 |
| 6 | 11 | 12 |
8.6 正则表达式匹配
8.6.1 题目
请实现一个函数用来匹配包含’. ‘和’‘的正则表达式。模式中的字符’.’表示任意一个字符，而’‘表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串”aaa”与模式”a.a”和”abaca”匹配，但与”aa.a”和”ab*a”均不匹配。
输入: s = “aa” p = “a” 输出: false 解释: “a” 无法匹配 “aa” 整个字符串。
输入: s = “aa” p = “a“ 输出: true 解释: 因为 ‘‘ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。
8.6.2 递推过程
虽然字符串的所有字符匹配整个模式，但是由于 * 的存在，接下来的匹配可能需要反复匹配，例如： s=a*a*bcdefg, p=aaaaaaabcdefg 。
从尾部开始看，设字符串长度为n，模式长度为m：
- 如果模式中第m个字符不是
*：- 模式的第m个字符与字符串第n个字符匹配，即最后的字符匹配，那么字符串是否匹配就取决于n-1的字符串与m-1的字符串是否匹配，例如
s=abc, p=abdc； - 如果最后的字符不匹配，那么最终的结果就是不匹配，例如
s=abc, p=abd。
- 模式的第m个字符与字符串第n个字符匹配，即最后的字符匹配，那么字符串是否匹配就取决于n-1的字符串与m-1的字符串是否匹配，例如
- 如果模型的第m个字符是*：
- 模式的第m-1个字符与字符串第n个字符匹配：
- 代表0，那么结果取决于n的字符串与m-2的模式匹配结果，例如： `s=abcc, p=abccc` ；
- 代表1，那么结果取决于n-1的字符串与m-2的模式匹配结果，但是由于应该代表的数字并不确认，可能取1、2、3……，所以此时应该保留，即最后的结果取决于n-1的字符串与m的模式匹配的结果，这样即使之后的匹配中不匹配也可以取0，而不会影响结果，例如： `s = abccc, p=abc` 。
- 两者不匹配，那么代表0才有可能出现匹配成功的结果，所以结果取决于n的字符串与m-2的模式匹配结果。例如： `s=abcd, p=abcde` 。
- 模式的第m-1个字符与字符串第n个字符匹配：
8.7 丑数
8.7.1 题目
我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。
输入: n = 10 输出: 12 解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
8.7.2 递推过程
一个丑数乘以2，3，5依然是丑数，即新添加了一个质因子。
设已知长度为 n 的丑数序列 x, x, …… , x，求第 n+1个丑数x。根根据递推性质，丑数x，只可能是以下三种情况其中之一（索引 a, b, c为未知数）：
由于 x__n+1 是 最接近 x__n 的丑数，因此索引 a, b, c 需满足以下条件：
若索引 a,b,c满足以上条件，则可使用递推公式计算下个丑数x__n+1 ，其为三种情况中的最小值，即：
x__n+1=min(x__a×2,x__b×3,x__c×5)
因此，可设置指针 a,b,c 指向首个丑数（即 1 ），循环根据递推公式得到下个丑数，并每轮将对应指针执行 +1 即可。因此，可设置指针 a,b,c指向首个丑数（即 11 ），循环根据递推公式得到下个丑数，并每轮将对应指针执行 +1即可。
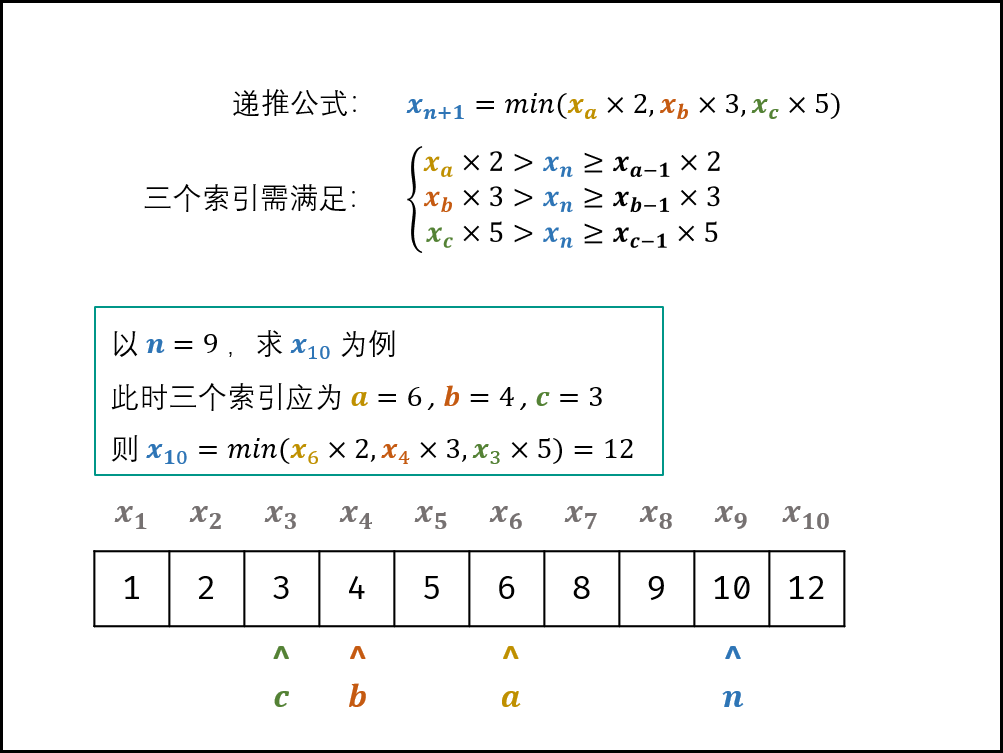
8.8 总结
动态规划基本步骤
- 找出最优解的性质，并刻划其结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息，构造最优解。
动态规划适用条件：
若有收获，就点个赞吧
0 人点赞
