线性代数是处理矩阵和向量空间的数学分支,在现代科学的各个领域都有应用。从某种意义上说,线性代数是一门语言,像对待外语一样,每天都学。David C.Lay的《线性代数及其应用》是非常棒的,内容既有深度,又有广度,讲得清晰易懂,又能联系实际应用,有大量的应用实例,内容结构安排的很好,前几章就引入子空间,向量,线性变换的概念,还介绍了一下线性代数的核心思想和研究内容,而后面几章的内容都紧扣这些概念。
《线性代数及其应用第5版》中文PDF,567页,带目录,文字可以复制,戴维C雷著,刘深泉译;第5版英文PDF,579页,带目录,文字可复制;第4版习题指导,485页。含有(第9章优化,56页,彩色配图,文字可复制;第10章有限状态马尔科夫链,78页,彩色配图,文字可复制)。
下载: https://pan.baidu.com/s/11vUHJ00BlQR9vWoMIB1aXg
提取码: 367z
线性代数的应用范围覆盖自然科学和社会科学的各个方面, 在处理高维问题时, 向量空间和矩阵运算更是这些学科的理论基础和基本工具.在计算机和经济管理等学科, 线性代数的重要性远远超过微积分.在学习传统线性代数课程时,大学生经常遇到学习抽象理论和应用矩阵万法的矛盾.在今天深化改革开放的环境下,大学生更应该了解线性代数课程的世界发展趋势和新的教学进展.
一个向量空间是由一些被称为向量的对象构成的非空集合V , 在这个集合上定义了两个运算,称为加法和标量来法(标量取实数),服从以下公理(或法则) θ , 这些公理必须对y 中所有向量u, v , W 及所有标量(或称数) c 和d 均成立.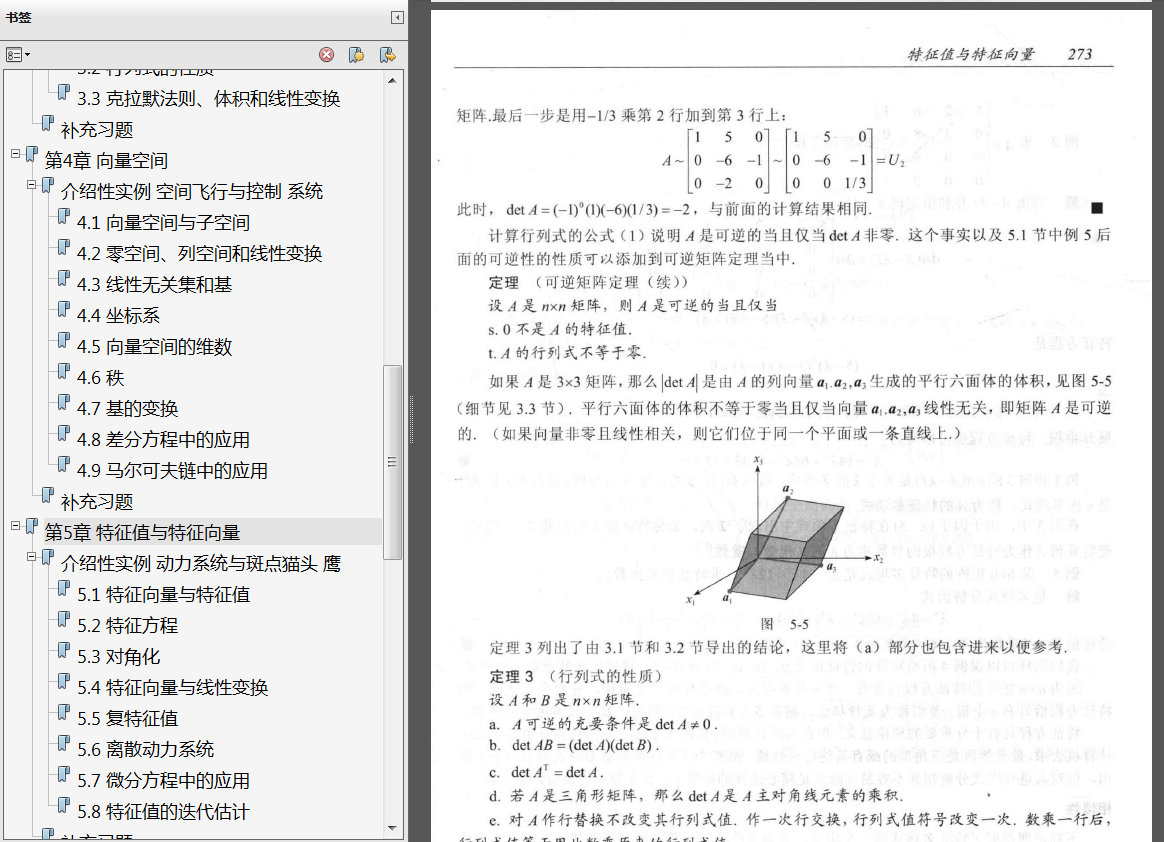
《线性代数及其应用第5版》是一本的现代教材,给出新的线性代数基本介绍和一些有趣应用,目的是帮助掌握线性代数的基本概念及应用技巧,为后续课程的学习和工作实践奠定基础。主要内容包括线性方程组、矩阵代数、行列式、向量空间、特征值与特征向量、正交性和小二乘法、对称矩阵和二次型、向量空间的几何学等,包含大量的练习题、习题、例题等,便于参考。
给我的感受就是完胜国内的线代教材。一些知识点,可以深入浅出,从多个维度进行解释,彼此之间相互关联。现在是二刷,内容既有深度,又有广度。讲得清晰易懂,又能联系实际应用。很好的入门和复习书,图片形象展示了数学工具也有物理意义。数形结合妙哉,而且还与计算机巧妙的结合起来。
一本让我觉得“哇,数学这么神奇”的书,粗浅地过了一遍。很适合入门,很适合工科。翻译也OK。一步一步,循序渐进。 由基础理论,到后面的正交分解,凸包,贝塞尔曲线,数学和研究的美感,淋漓尽致。
我的感受是从事数据处理和数据分析、优化的朋友,一定要学好数学,尤其是线性代数。一些知识点,可以深入浅出,从多个维度进行解释,彼此之间相互关联。一步一步,循序渐进。 由基础理论向量空间,到后面的正交分解,凸包,贝塞尔曲线,数学和研究的美感,淋漓尽致。
掌握线性代数的基本概念及应用技巧,为后续课程的学习和工作实践奠定基础。
线性代数是一种语言,必须用学习外语的方法每天学习这种语言,理解每一节的内容并不容易,讲得清晰易懂,又能联系实际应用,有大量的应用实例,内容结构安排的很好,前几章就引入子空间,向量,线性变换的概念,还介绍了一下线性代数的核心思想和研究内容。
《线性代数及其应用》给出新的线性代数基本介绍和一些有趣应用,目的是帮助掌握线性代数的基本概念及应用技巧,为后续课程的学习和工作实践奠定基础。主要内容包括线性方程组、矩阵代数、行列式、向量空间、特征值与特征向量、正交性和最小二乘法、对称矩阵和二次型、向量空间的几何学等。

