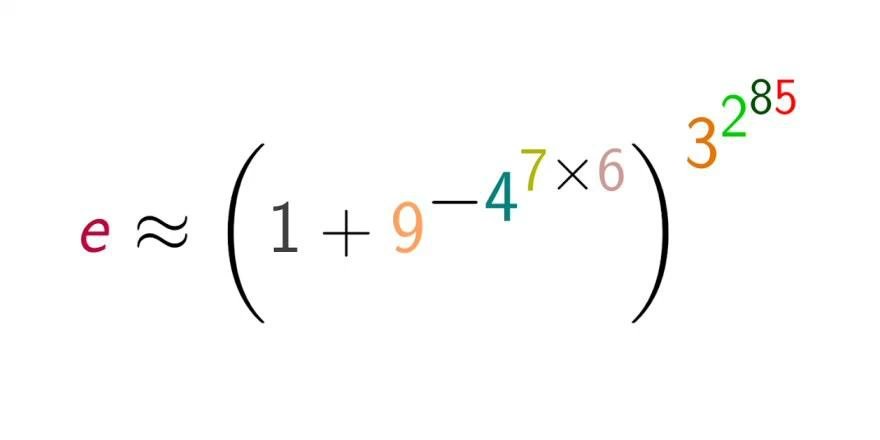2014-11-04 16:49:08 <br /> <br /> 用数字1到9,每个只能用一次,我们需要得到一个e的近似值。知道为什么它会特别近似吗?
Approximating e using the digits 1─9
The number e (approximately 2.718281828459045) is one of the most important irrational numbers in mathematics, being the base of the natural logarithm. Remarkably, it is possible to get a stunningly accurate approximation to e using the digits 1 up to 9, exactly once each, together with the standard operations of addition, negation, multiplication and exponentiation. According to the formula in the picture, e is close to
(1 + 9^{─4^{7x6}})^{3^{2^{85}}}.
So why does this work? The key to understanding what is going on is the number N=3^{2^{85}}, an astronomically huge number. The number N appears more subtly in another place in the formula, because 4^{7x6}, or 4^{42}, is equal to 2^{84}. Since 9 is 3^2, it follows that 9^{4^{7x6}} is equal to {3^2}^{2^{84}}, which is equal to 3^{2x(2^{84})}, or 3^{2^{85}}. This means that 9^{─4^{7x6}} is equal to 1/N.
In summary, the formula in the picture is equal to (1+1/N)^N for a really large value of N. The limit of this formula, as N tends to infinity, is well known to be exactly equal to e.
I’d be interested to know where this formula originally came from. I found it on twitter via Colin Beveridge and Chris Smith. Chris Smith says that the approximation is accurate to over 1.8x10^{25} decimal places. I haven’t checked this, but it is certainly a very accurate approximation.
这个公式利用(1+1/n)^n 的极限是 e 这个特性。漂亮。最重要的是这个近似不是一般的近似,已经到了不可思议的地步。准确位数是1.8X10^25。注意,不是25位数,是10^25位数。全世界的纸用光也印不出这么多位数。
我说那式子精确度是1.8X10^25。有很多人问,既然全世界的纸用完都写不出那么多位数,你也不能算到那么多位,你是怎么知道的。有定理说用(1+1/n)^n逼近e,其误差与e/n同阶,这里n=3^(2^85),取对数即可。这就是数学的强大。运筹于帷幄之中,决胜于千里之外。