写在前面

JS中涉及到的对数值的操作：算数运算（加减乘除）+逻辑运算（比较）+转换类型
常见的坑有

  • 纯数值运算：值域的上下界，是否支持精确计算（0.1+0.2！=0.3）
  • 大小与相等比较：
  • 数字转字符串：较大数字的科学计数法问题
  • 类型转换中NAN问题

1.前置知识

参考此文章 http://jser.it/blog/2014/07/07/numbers-in-javascript/

  • 数据表示
    （1）使用什么进制（2，8，16？）
    （2）正负号的问题：原码，补码，反码
    （3）小数点在哪里：定点OR浮点
  • -123.456 === -1.23456 × 10^2
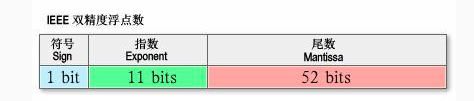
    提升JS质量—1. JS的Numbers - 图1

总结

JS中的数值 由一个符号位+11个指数为+52个尾数位组成

2.1JS值的范围

  • 整数最多有53位来表示
    [-9007199254740991,9007199254740991] === [-2^53 - 1,2^53 - 1] ===[Number.MIN_VALUE,Number.MAX_VALUE]
  • 有些数字操作（入位操作）只使用与32位
    只支持到约21亿大小的数字

2.2 数值检测

  1. Number.isSafeInteger( Number.MAX_SAFE_INTEGER );    // true 
  2. Number.isSafeInteger( Math.pow( 2, 53 ) );          // false 
  3. Number.isSafeInteger( Math.pow( 2, 53 ) - 1 );      // true

2.3 极大与极小数字采用科学计数法表示

  1. var a = 5E10; a;      // 50000000000 a.toExponential();  // "5e+10" 
  2. var b = a * a; b;         // 2.5e+21 
  3. var c = 1 / a; c;        // 2e-11

指数表示后转换为字符串

  1. b.toString() // "2.5e+21"

解决方案

2.4浮点数的坑

浮点数只能表示有限精度的数字，只有近似结果。有效的解决办法是尽量采用整数运算

  • 原因：采用了IEEE754 数值的浮点计算
    IEEE754是二进制的规则，所以可以看做用n*2m类型数字，所以很简单的0.1无法被准确的表
    示。
  • 解析：计算机世界只有01没有小数
    二进制，每位的维权是 2^(n-1),整数部分依次为1,2,4,8,16等，小数部分为0.5,0.25,0.125,0.0625等，所以你无法精确的表示某些小数

2.5 特殊值

3. JS动态类型语言

JS是弱类型，动态类型,不同类型数据运算有隐患，本来该抛出的错误你都不抛出了

A1.强类型：偏向于不容忍隐式类型转换。譬如说haskell的int就不能变成double A2.弱类型：偏向于容忍隐式类型转换。譬如说C语言的int可以变成double B1.静态类型：编译的时候就知道每一个变量的类型，因为类型错误而不能做的事情是语法错误。 B2.动态类型：编译的时候不知道每一个变量的类型，因为类型错误而不能做的事情是运行时错误。譬如说你不能对一个数字a写a[10]当数组用。 作者：vczh链接：https://www.zhihu.com/question/19918532/answer/21645395

  • null算数运算中被转为0；NAN会继续参与运算，调试噩梦
  • 判断NAN
    var x =NaN
    x === NaN false
    这样不可行。标准库也不靠谱。
    isNaN(“foo”) true
    var a = NaN
    a !==a true
    var b = “foo”
    b !==b //false