二叉树：
    每个节点最多有2个子节点

    二叉搜索树（BST）：二叉树的一种
    左子树中所有的节点都比跟节点小，右子树所有的节点都比跟节点大

    下图：展现了一棵二叉搜索树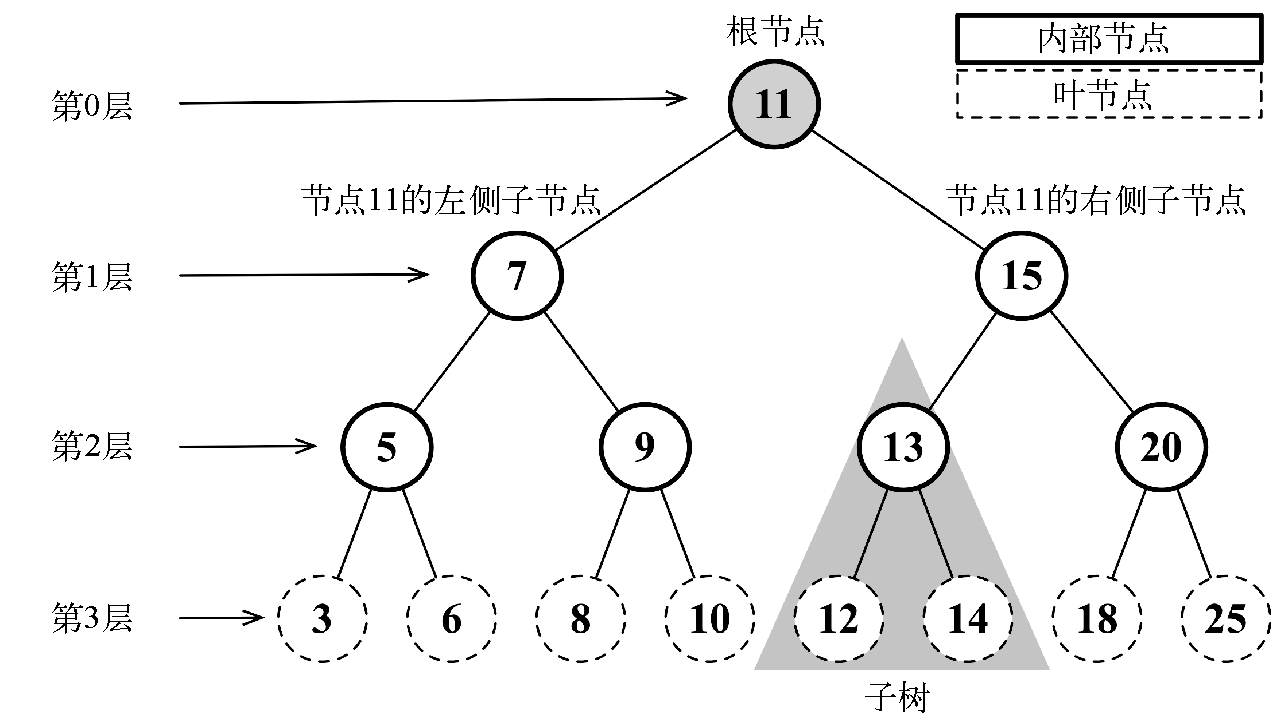
    image.png

    算法：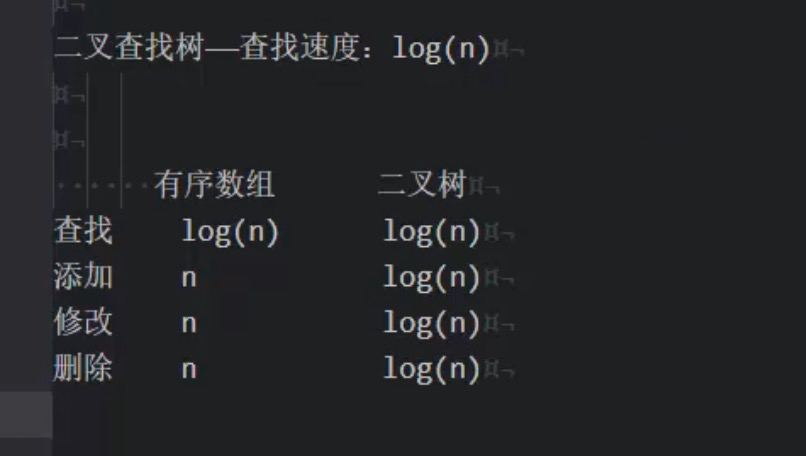
    image.png

    二叉树的实现

    3.     class BST{
    4.       constructor() {
    5.         this.root = null;
    6.       }
    8.       // 插入
    9.       insert(key, value) {
    10.         // 如果有根
    11.         if(!this.root) {
    12.           this.root = new BSTNode(key, value);
    13.         } else {
    14.           insert(this.root);
    15.         }
    17.         function insert(node){
    18.           if(node.key === key) {
    19.             throw new Error ('不能重复')
    20.           } else {
    21.             // 往右走
    22.             if(node.key < key) {
    23.               if(!node.right) {
    24.                 node.right = new BSTNode(key, value);
    25.               } else {
    26.                 // 继续比较
    27.                 insert(node.right);
    28.               }
    29.             } else {
    30.               // 往左走
    31.               if(!node.left) {
    32.                 node.left = new BSTNode(key, value);
    33.               } else {
    34.                  // 继续比较
    35.                 insert(node.left);
    36.               }
    37.             }
    38.           }
    39.         }
    40.       }
    42.       // 查询
    43.       search(key) {
    44.         if(!this.root) {
    45.           return undefined;
    46.         } else {
    47.           return search(this.root);
    48.         }
    50.         function search(node) {
    51.           // 如果node是空节点
    52.           if(!node) return undefined;
    54.           if(node.key === key) {
    55.             return node.value;
    56.           } else {
    57.             if(node.key < key) {
    58.               // 往右查询
    59.               return search(node.right);
    60.             } else {
    61.               // 往左查询
    62.               return search(node.left);
    63.             }
    64.           }
    65.           // 最终没找到返回 
    66.           return undefined;
    67.         }
    68.       }
    70.     }
    72.     class BSTNode {
    73.       constructor(key, value) {
    74.         this.key = key;
    75.         this.value = value;
    76.         this.left = null;
    77.         this.right = null;
    78.       }
    79.     }
    81.     const tree = new BST();
    82.     tree.insert(16, 'aa');
    83.     tree.insert(2, 'bb');
    84.     tree.insert(20, 'cc');
    85.     tree.insert(13, 'dd');
    86.     tree.insert(8, 'ee');
    87.     tree.insert(4, 'ff');
    88.     tree.insert(25, 'gg');
    90.     console.log(tree.search(20));
    91.     console.log(tree);

    二叉树 - 遍历

    树 - 遍历
    1.把所有数据都走一遍
    2.数据持久化

    1.   树遍历<br />      深度优先、广度优先
    3.   二叉树树遍历<br />      前序：当前节点 ，left, right<br />      中序：left, 当前节点， right<br />      后序： left , right , 当前节点
    5.   二叉排序<br />      1.把数据随机插入<br />      2.按照“中序遍历“的顺序，把数据重新遍历出来
    1. class BST{
    2.       constructor() {
    3.         this.root = null;
    4.       }
    6.       // 插入
    7.       insert(key, value) {
    8.         // 如果有根
    9.         if(!this.root) {
    10.           this.root = new BSTNode(key, value);
    11.         } else {
    12.           insert(this.root);
    13.         }
    15.         function insert(node){
    16.           if(node.key === key) {
    17.             throw new Error ('不能重复')
    18.           } else {
    19.             // 往右走
    20.             if(node.key < key) {
    21.               if(!node.right) {
    22.                 node.right = new BSTNode(key, value);
    23.               } else {
    24.                 // 继续比较
    25.                 insert(node.right);
    26.               }
    27.             } else {
    28.               // 往左走
    29.               if(!node.left) {
    30.                 node.left = new BSTNode(key, value);
    31.               } else {
    32.                  // 继续比较
    33.                 insert(node.left);
    34.               }
    35.             }
    36.           }
    37.         }
    38.       }
    40.       // 查询
    41.       search(key) {
    42.         if(!this.root) {
    43.           return undefined;
    44.         } else {
    45.           return search(this.root);
    46.         }
    48.         function search(node) {
    49.           // 如果node是空节点
    50.           if(!node) return undefined;
    52.           if(node.key === key) {
    53.             return node.value;
    54.           } else {
    55.             if(node.key < key) {
    56.               // 往右查询
    57.               return search(node.right);
    58.             } else {
    59.               // 往左查询
    60.               return search(node.left);
    61.             }
    62.           }
    63.           // 最终没找到返回 
    64.           return undefined;
    65.         }
    66.       }
    69.       // 中序遍历 left, 当前节点， right，遍历后数据
    70.       walk(fn){
    71.         if(!this.root) {
    72.           return;
    73.         } else {
    74.           return walk(this.root);
    75.         }
    77.         function walk(node) {
    78.           if(!node) return;
    79.           else {
    80.             walk(node.left);
    81.             fn(node);
    82.             walk(node.right)
    83.           }
    84.         }
    85.       }
    87.     }
    89.     class BSTNode {
    90.       constructor(key, value) {
    91.         this.key = key;
    92.         this.value = value;
    93.         this.left = null;
    94.         this.right = null;
    95.       }
    96.     }
    98.     const tree = new BST();
    99.     // 随机插入
    100.     tree.insert(16, 'aa');
    101.     tree.insert(2, 'bb');
    102.     tree.insert(20, 'cc');
    103.     tree.insert(13, 'dd');
    104.     tree.insert(8, 'ee');
    105.     tree.insert(4, 'ff');
    106.     tree.insert(25, 'gg');
    107.     tree.insert(3, 'hh');
    108.     tree.insert(45, 'hh');
    109.     tree.insert(23, 'hh');
    110.     tree.insert(18, 'hh');
    112.     console.log(tree);
    113.     // 遍历
    114.     tree.walk(node => console.log(node.key, node.value));