链表

参考博客：https://blog.csdn.net/a984500801/article/details/123019369

基本内容

数组开辟一片连续空间存储，通过索引直接访问元素。 静态数组在初始化得知道元素数量，我们可以用动态数组，但是未能充分利用全部空间。
链表是由多个结点构成。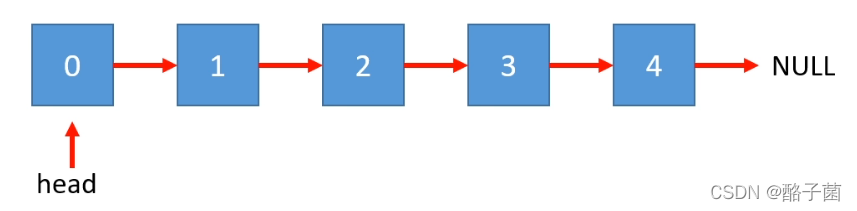

查找元素需要获得上一个结点引用。

private class Node
{
    public E e;         //结点存储的元素
    public Node next;   //下一个结点的引用(指针)
}
private Node head;      //链表中头结点的引用

相关操作

添加修改删除节点

参考上方博客

反转链表

即给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头，例如给定1，2，3返回3，2，1
双链表求解
把原链表的结点一个个摘掉，每次摘掉的链表都让他成为新的链表的头结点，然后更新新链表。下面以链表1→2→3→4为例画个图来看下。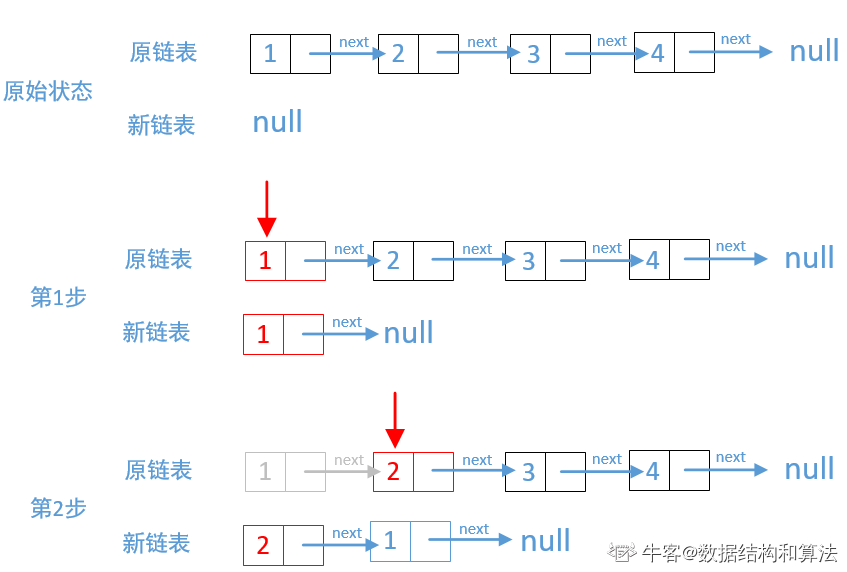

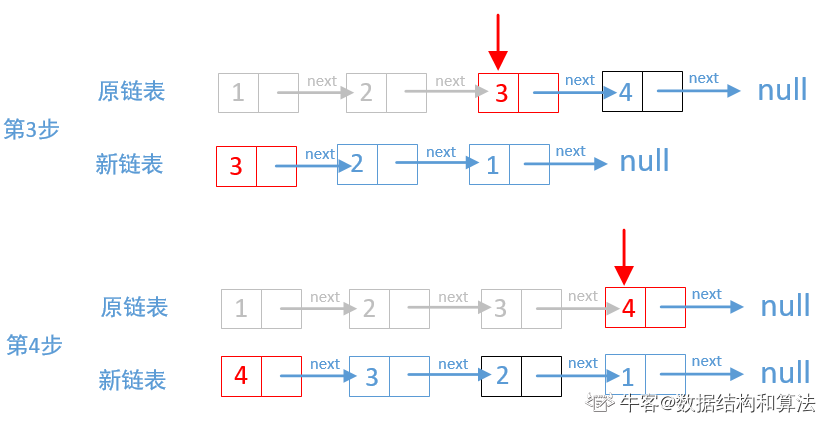
public class ListNode
{
    public int val;
    public ListNode next;
    public ListNode (int x)
    {
        val = x;
    }
}*/
class Solution
{
    public ListNode ReverseList(ListNode pHead)
    {
        ListNode dst = null;
        ListNode cur =null;
        while (pHead != null)
        {
            cur = pHead;
            pHead = pHead.next;
            cur.next = dst;
            dst = cur;
        }
        return dst;
    }
}

二叉树

参考：https://blog.csdn.net/qq_34035956/article/details/104036671

基本内容

二叉树(binary tree)是树的一种特殊形式。二叉，指的是这种树的每个节点最多有2个孩子节点。这里最多有2个，也可能只有1个，或者没有孩子节点。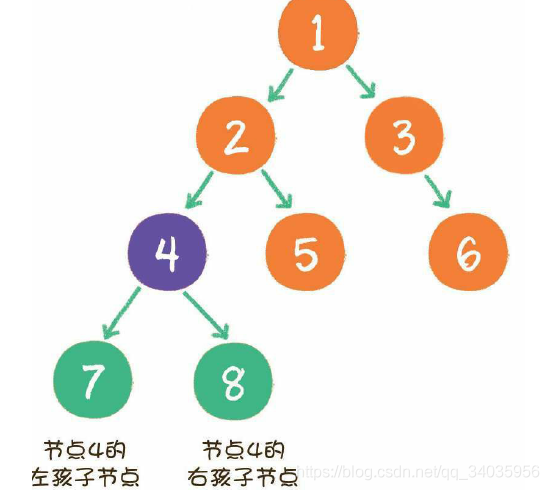

二叉树可以用链式存储和数组两种物理存储结构来表达。

• 链式存储

二叉树的一个节点最多指向左右两个孩子节点，所以二叉树一个节点包含3部分;
1.存储数据的data变量
2.指向左孩子的left指针
3.指向右孩子的right指针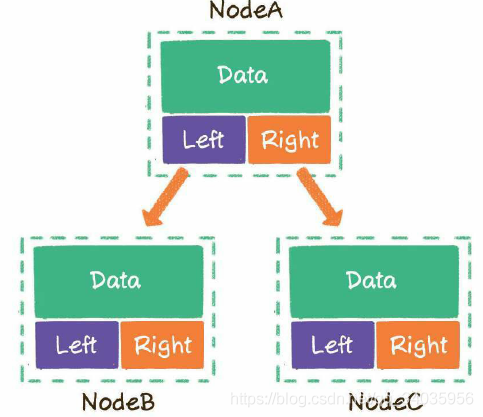

• 数组存储

使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子和右孩子空缺，则数组的相应位置也空出来。
假设一个父节点的下标是parent，那么它的左孩子节点下标就是2parent+1；右孩子节点下标是2parent+2。反过来，一个左孩子的节点下标是leftChild，那么父节点下标就是(leftChild-1)/2。

查找操作

查找：二叉查找树(binary search tree)
二叉查找树在二叉树的基础上增加了以下几个条件：
1、若左子树不为空，则左子树所有节点的值均小于根节点的值；
2、若右子树不为空，则右子树所有节点的值均大于根节点的值；
3、左、右子树也都是二叉查找树。
二叉查找树要求左子树小于父节点，右子树大于父节点，这样保证了二叉树的有序性，因此 二叉查找树也叫二叉排序树。
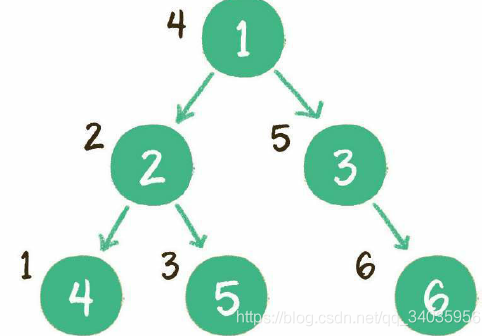
新插入的节点，遵循二叉排序树的原则：例如插入新元素5，由于5<6，5>3,5>4，所以5最终会插入到节点4的右孩子位置。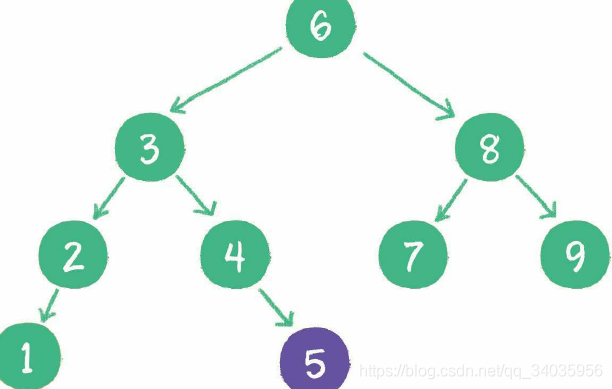

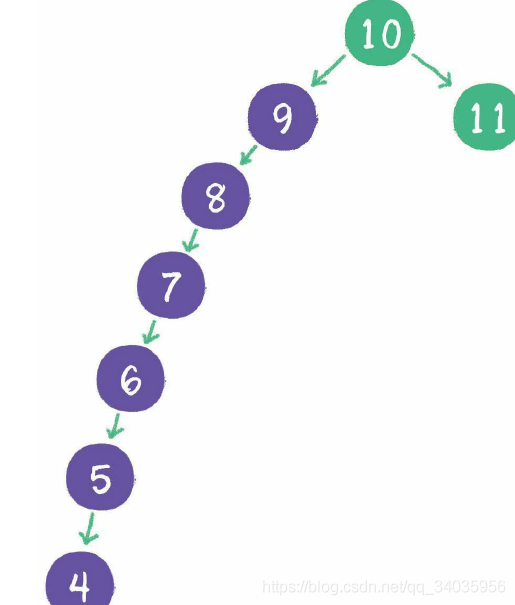
二叉堆：只要求父节点比它的左右孩子都大。

二叉树遍历

从节点之间位置关系的角度看，二叉树的遍历可分为4种：
1.前序遍历：根节点、左子树、右子树。
2.中序遍历：左子树、根节点、右子树
3.后序遍历：左子树、右子树、根节点
4.层序遍历：一层一层遍历
从更宏观的角度看，二叉树的遍历归结为两大类。
1.深度优先遍历（前序遍历、中序遍历、后序遍历）。偏向于纵深，一头扎下去。
2.广度优先遍历（层序遍历）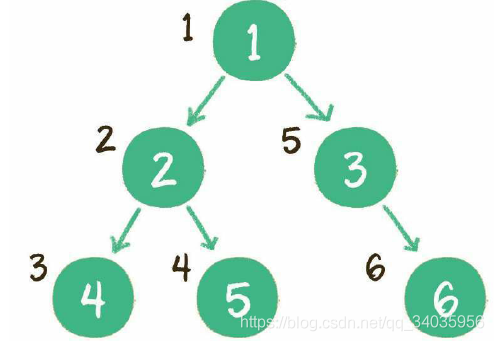

先序、中序、后序遍历

二维数组输出先序、中序、后序遍历

using System;
using System.Collections.Generic;
public class TreeNode
{
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode (int x)
    {
        val = x;
    }
}
class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * @param root TreeNode类 the root of binary tree
     * @return int整型二维数组
     */
    public List<List<int>> threeOrders (TreeNode root) {
        // write code here
        List<List<int>> quanbu = new List<List<int>>();
        List<int> xianxu = new List<int>();
        List<int> zhongxu = new List<int>();
        List<int> houxu = new List<int>();
        preOrder(root, xianxu);
        midOrder(root, zhongxu);
        posOrder(root, houxu);
        quanbu.Add(xianxu);
        quanbu.Add(zhongxu);
        quanbu.Add(houxu);
        return quanbu;
    }
    public void preOrder(TreeNode root,List<int> xianxu)
    {
            if(root == null)return;
            xianxu.Add(root.val);
            if(root.left != null)preOrder(root.left,xianxu);
            if(root.right != null)preOrder(root.right,xianxu);
    }
    public void midOrder(TreeNode root,List<int> zhongxu)
    {
            if(root == null)return;
            if(root.left != null)midOrder(root.left,zhongxu);
            zhongxu.Add(root.val);
            if(root.right != null)midOrder(root.right,zhongxu);
    }
    public void posOrder(TreeNode root,List<int> houxu)
    {
            if(root == null)return;
            if(root.left != null)posOrder(root.left,houxu);
            if(root.right != null)posOrder(root.right,houxu);
            houxu.Add(root.val);
    }
}

用递归实现前、中、后序是最自然的方式，3种遍历方式的区别仅仅是输出的执行位置不同：前序遍历的输出在前，中序遍历的输出在中间，后序遍历的输出在最后。
二叉树的构建方式很多，这里把一个线性的链表转化成非线性的二叉树。
可以用递归解决的方法，同样可以用栈解决，递归和栈都有回溯的特性。

层序遍历

using System;
using System.Collections.Generic;
public class TreeNode
{
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode (int x)
    {
        val = x;
    }
}
class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * @param root TreeNode类 
     * @return int整型二维数组
     */
    public List<List<int>> levelOrder (TreeNode root) {
        // write code here
        List<List<int>> resurt = new List<List<int>>();
        Queue<TreeNode> queue = new Queue<TreeNode>();
        queue.Enqueue(root);
        while(queue.Count > 0)
        {
            List<int> temp = new List<int>();
            int len = queue.Count;
            while(len > 0)
            {
                TreeNode node = queue.Dequeue();
                temp.Add(node.val);
                if(node.left != null)
                {
                    queue.Enqueue(node.left);
                }
                if(node.right != null){
                    queue.Enqueue(node.right);
                }
                len--;
            }
            resurt.Add(temp);
        }
        return resurt;
    }
}

栈Stack和队列Queue

栈是先进后出；队列是先进先出。
栈只有两种操作，push（入栈，插入数据）和pop（出栈，删除数据）。用数组实现的栈叫顺序栈，用链表实现的栈叫链式栈
队列：Enqueue（入队，插入数据）和Dequeue（出队，删除数据）。用数组实现的栈叫顺序队列，用链表实现的栈叫链式队列
案例
用两个栈来实现一个队列，使用n个元素来完成 n 次在队列尾部插入整数(push)和n次在队列头部删除整数(pop)的功能。 队列中的元素为int类型。保证操作合法，即保证pop操作时队列内已有元素。
输入：
[“PSH2”,”PSH3”,”POP”,”PSH1”,”POP”,”POP”]
返回值：
321

using System.Collections.Generic;
class Solution
{
    Stack<int> sk1 = new Stack<int>();
    Stack<int> sk2 = new Stack<int>();
    public void push(int node) 
    {
        while(sk2.Count>0)
        {
            sk1.Push(sk2.Pop());
        }
        sk1.Push(node);
    }
    public int pop() 
    {
        while(sk1.Count>0)
        {
            sk2.Push(sk1.Pop());
        }
        return sk2.Pop();
    }
}