负载均衡
负载均衡(load balance)是一种在多个计算机(网络、CPU、磁盘)之间均匀分配资源,以提高资源利用率的技术。在分布式项目中,为了提高系统的可用性,服务提供者一般都会做集群处理,当其中一个服务出现宕机的时候,集群的其他服务仍然能够提供服务,从而提高系统的可靠性。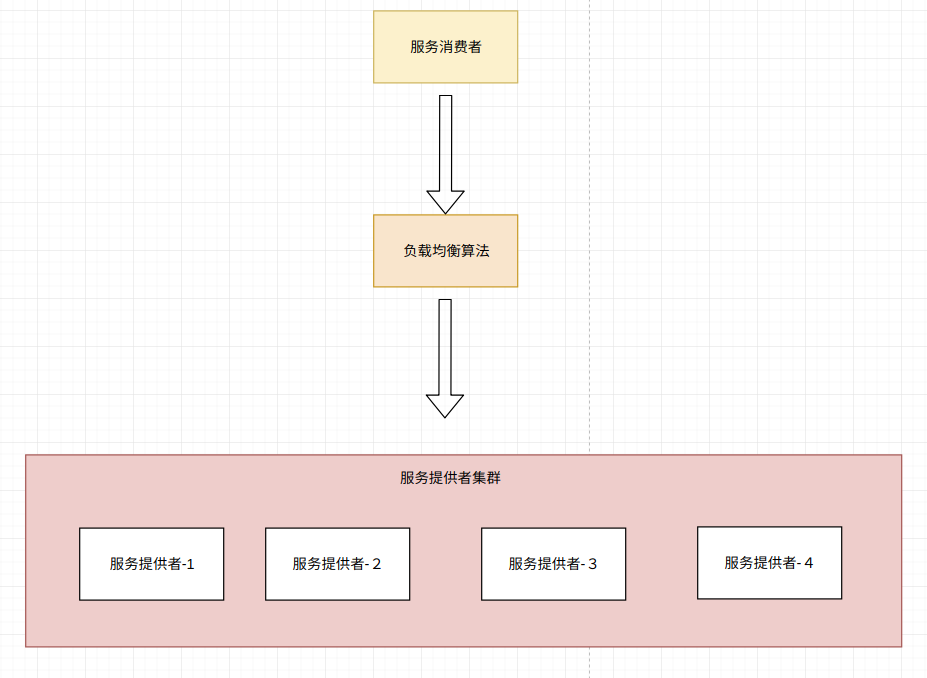
从负载均衡设备的角度来看,分为硬件负载均衡和软件负载均衡:
硬件负载均衡:比如最常见的F5,还有Array等,这些负载均衡是商业的负载均衡器,性能比较好,毕竟他们的就是为了负载均衡而生的,背后也有非常成熟的团队,可以提供各种解决方案,但是价格比较昂贵。
软件负载均衡:包括我们耳熟能详的Nginx,LVS,Tengine(阿里对Nginx进行的改造)等。优点就是成本比较低,但是也需要有比较专业的团队去维护,要自己去踩坑,去DIY。
从负载均衡的技术来看,分为服务端负载均衡和客户端负载均衡:
服务端负载均衡:当我们访问一个服务,请求会先到负载均衡服务器,然后这台服务器会把请求分发到后台服务器,当然如果只有一台服务器,那好说,直接把请求给那一台服务器就可以了,但是如果有多台服务器呢?这时候,就会根据一定的算法选择一台服务器。
客户端负载均衡:客户端服务均衡的概念貌似是有了服务治理才产生的,简单的来说,就是在一台服务器上维护着所有服务的ip,名称等信息,当我们在代码中访问一个服务,是通过一个组件访问的,这个组件会从那台服务器上取到所有提供这个服务的服务器的信息,然后通过一定的算法,选择一台服务器进行请求。
负载均衡算法主要有六种:轮询法、随机法、源地址哈希法、加权轮询法、加权随机法、最小连接数法。
轮询算法
将请求按顺序轮流地分配到后端服务器上,它均衡地对待后端的每一台服务器,而不关心服务器实际的连接数和当前的系统负载。在实现时,轮询算法通常是把所有可节点放到个数组,然后按照数组编号,挨个访问。
如服务有10个节点,放到数组就是个大小为10的数组,这样的话就可以从序号为0的节点开始访问,访问后序号动加1,下次就会访问序号为1的节点,以此类推。轮询算法能够保证所有节点被访问到的概率是相同的。
加权轮询算法
轮询算法能够保证所有节点被访问的概率相同,加权轮询算法是在此基础上,给每个节点赋予个权重,从而使每个节点被访问到的概率不同,权重越大的节点被访问的概率越大。在实现时,我们可以生成n+1个从0到n的数字,依次选择这n+1个数,假如A,B,C的权重分别为5,6,8,可以把这三个权重分为三个区间。
1———5———11————-19。
A B C
假如数字在第一个区间,则可以选择A,第二个区间,则可以选择B,第三个区间,可以选择C,依次类推,如果数组大于19,则可以将n%19。这样便可以实现AAAAABBBBBBCCCCCCCC。
但是该实现有一个问题,就是前几次的选择都是A,只有达到权重的个数之后,才能访问下一个,从而造成某一个时间段访问某一个节点的频率高。所以需要进行平滑。
平滑加权轮询算法
假如A服务器的权重是5,B服务器的权重是1,C服务器的权重是1。
这个权重,我们称之为“固定权重”,既然这个叫“固定权重”,那么肯定还有叫“非固定权重的”,没错,“非固定权重”每次都会根据一定的规则变动。
- 第一次访问,ABC的“非固定权重”分别是 5,1,1(初始),因为5是其中最大的,5对应的就是A服务器,所以这次选到的服务器就是A,然后我们用当前被选中的服务器的权重-各个服务器的权重之和,也就是A服务器的权重-各个服务器的权重之和。也就是5-7=-2,没被选中的服务器的“非固定权重”不做变化,现在三台服务器的“非固定权重”分别是-2,1,1。
- 第二次访问,把第一次访问最后得到的“非固定权重”+“固定权重”,现在三台服务器的“非固定权重”是3,2,2,因为3是其中最大的,3对应的就是A服务器,所以这次选到的服务器就是A,然后我们用当前被选中的服务器的权重-各个服务器的权重之和,也就是A服务器的权重-各个服务器的权重之和。也就是3-7=-4,没被选中的服务器的“非固定权重”不做变化,现在三台服务器的“非固定权重”分别是-4,1,。
- 第三次访问,把第二次访问最后得到的“非固定权重”+“固定权重”,现在三台服务器的“非固定权重”是1,3,3,这个时候3虽然是最大的,但是却出现了两个,我们选第一个,第一个3对应的就是B服务器,所以这次选到的服务器就是B,然后我们用当前被选中的服务器的权重-各个服务器的权重之和,也就是B服务器的权重-各个服务器的权重之和。也就是3-7=-4,没被选中的服务器的“非固定权重”不做变化,现在三台服务器的“非固定权重”分别是1,-4,3。
…
以此类推,最终得到这样的表格:
| 请求 | 获得服务器前的非固定权重 | 选中的服务器 | 获得服务器后的非固定权重 |
|---|---|---|---|
| 1 | {5, 1, 1} | A | {-2, 1, 1} |
| 2 | {3, 2, 2} | A | {-4, 2, 2} |
| 3 | {1, 3, 3} | B | {1, -4, 3} |
| 4 | {6, -3, 4} | A | {-1, -3, 4} |
| 5 | {4, -2, 5} | C | {4, -2, -2} |
| 6 | {9, -1, -1} | A | {2, -1, -1} |
| 7 | {7, 0, 0} | A | {0, 0, 0} |
| 8 | {5, 1, 1} | A | {-2, 1, 1} |
当第8次的时候,“非固定权重“又回到了初始的5,1,1,nginx采用的便是这种算法。
随机法
通过系统的随机算法,根据后端服务器的列表大小值来随机选取其中的一台服务器进行访问。由概率统计理论可以得知,随着客户端调用服务端的次数增多,其实际效果越来越接近于平均分配调用量到后端的每一台服务器,也就是轮询的结果。
加权随机法
与加权轮询法一样,加权随机法也根据后端机器的配置,系统的负载分配不同的权重。不同的是,它是按照权重随机请求后端服务器,而非顺序。
最小连接数法
最小连接数算法比较灵活和智能,由于后端服务器的配置不尽相同,对于请求的处理有快有慢,它是根据后端服务器当前的连接情况,动态地选取其中当前积压连接数最少的一台服务器来处理当前的请求,尽可能地提高后端服务的利用效率,将负责合理地分流到每一台服务器。
源地址哈希法
考虑到一种情况,假如用户userA在某个网站上进行购物,首先登陆,负载均衡服务器将userA的请求分配给服务器A,后续userA将商品加入购物车,然后进行支付请求,此次的请求由负载均衡服务器分配给了服务器B,但是服务器B中由于没有userA登陆信息的session,就判定userA没有登陆。当然,可以采用redis来session同步。一致性哈希算法也可以解决该问题。
一致性Hash算法也是使用取模的方法,不过,上述的取模方法是对服务器的数量进行取模,而一致性的Hash算法是对2的32方取模。即,一致性Hash算法将整个Hash空间组织成一个虚拟的圆环,Hash函数的值空间为0 ~ 2^32 - 1(一个32位无符号整型),整个哈希环如下:
Hash圆环
整个圆环以顺时针方向组织,圆环正上方的点代表0,0点右侧的第一个点代表1,以此类推。
第二步,我们将各个服务器使用Hash进行一个哈希,具体可以选择服务器的IP或主机名作为关键字进行哈希,这样每台服务器就确定在了哈希环的一个位置上,比如我们有三台机器,使用IP地址哈希后在环空间的位置如图1-4所示:
图1-4:服务器在哈希环上的位置
现在,我们使用以下算法定位数据访问到相应的服务器:
将数据Key使用相同的函数Hash计算出哈希值,并确定此数据在环上的位置,从此位置沿环顺时针查找,遇到的服务器就是其应该定位到的服务器。
例如,现在有ObjectA,ObjectB,ObjectC三个数据对象,经过哈希计算后,在环空间上的位置如下:

图1-5:数据对象在环上的位置
根据一致性算法,Object -> NodeA,ObjectB -> NodeB, ObjectC -> NodeC
一致性Hash算法的容错性和可扩展性
现在,假设我们的Node C宕机了,我们从图中可以看到,A、B不会受到影响,只有Object C对象被重新定位到Node A。所以我们发现,在一致性Hash算法中,如果一台服务器不可用,受影响的数据仅仅是此服务器到其环空间前一台服务器之间的数据(这里为Node C到Node B之间的数据),其他不会受到影响。如图1-6所示:

图1-6:C节点宕机情况,数据移到节点A上
另外一种情况,现在我们系统增加了一台服务器Node X,如图1-7所示:

图1-7:增加新的服务器节点X
此时对象ObjectA、ObjectB没有受到影响,只有Object C重新定位到了新的节点X上。
如上所述:
一致性Hash算法对于节点的增减都只需重定位环空间中的一小部分数据,有很好的容错性和可扩展性。
数据倾斜问题
在一致性Hash算法服务节点太少的情况下,容易因为节点分布不均匀面造成数据倾斜(被缓存的对象大部分缓存在某一台服务器上)问题,如图1-8特例:
图1-8:数据倾斜
这时我们发现有大量数据集中在节点A上,而节点B只有少量数据。为了解决数据倾斜问题,一致性Hash算法引入了虚拟节点机制,即对每一个服务器节点计算多个哈希,每个计算结果位置都放置一个此服务节点,称为虚拟节点。
具体操作可以为服务器IP或主机名后加入编号来实现,实现如图1-9所示:
图1-9:增加虚拟节点情况
数据定位算法不变,只需要增加一步:虚拟节点到实际点的映射。
所以加入虚拟节点之后,即使在服务节点很少的情况下,也能做到数据的均匀分布。

