1、排序算法说明

1.1 排序的定义

对一序列对象根据某个关键字进行排序。

1.2 术语说明

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
• 内排序：所有排序操作都在内存中完成；
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
• 时间复杂度： 一个算法执行所耗费的时间。
• 空间复杂度：运行完一个程序所需内存的大小。

1.3 算法总结

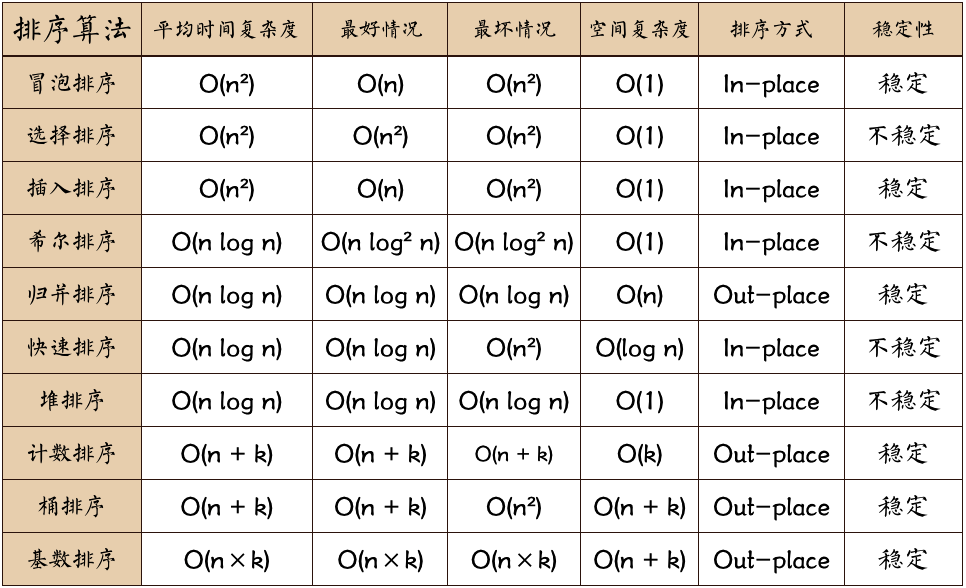
image.png

  • n: 数据规模
  • k: “桶”的个数
  • In-place: 占用常数内存，不占用额外内存
  • Out-place: 占用额外内存

    2、排序算法

    2.1 冒泡排序

  1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
  3. 针对所有的元素重复以上的步骤，除了最后一个；
  4. 重复步骤1~3，直到排序完成。

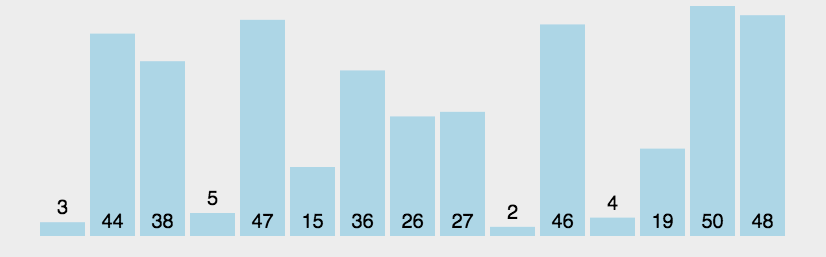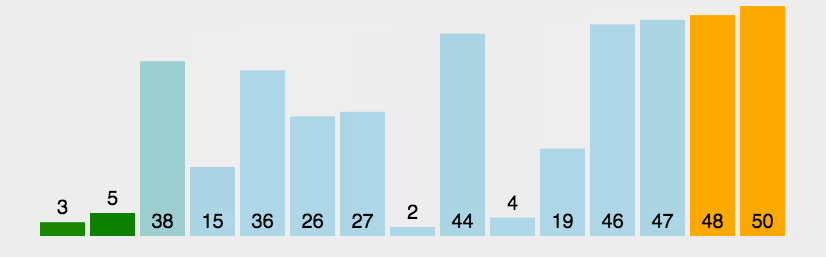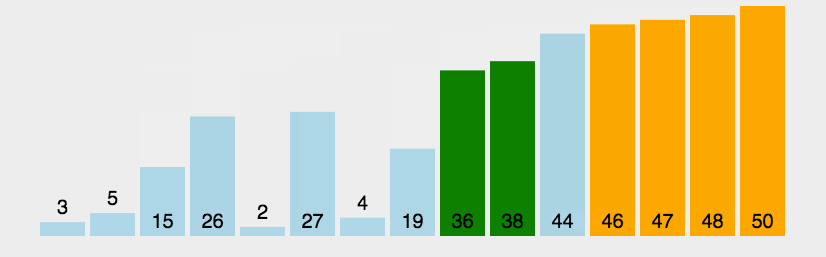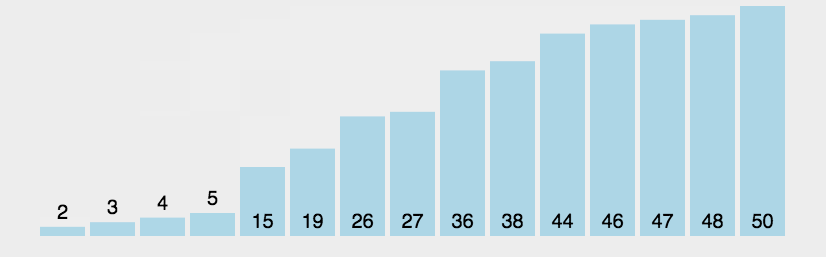
1595259433251-b914e77b-fcb2-4b40-8a12-262d3e142d74.gif

  1. #pragma once
  2. #include <iostream>
  3. using namespace std;
  4. void bubbleSort(int arr[], int n)
  5. {
  6.     for (int i = 0; i < n; i++)
  7.     {    
  8.         int swapFlag = 0;//是否进行了交换(该方式是为了避免有序数组还要进行遍历）
  10.         for (int j = 0; j < n - i - 1; j++)
  11.         {
  12.             if (arr[j] > arr[j + 1])
  13.             {
  14.                 swapFlag = 1;
  15.                 swap(arr[j], arr[j + 1]);
  16.             }
  17.         }
  18.         if (swapFlag == 0)
  19.         {
  20.             return;
  21.         }
  22.     }
  23. }

最佳情况：T(n) = O(n) 最差情况：T(n) = O(n2) 平均情况：T(n) = O(n2)

2.2 鸡尾酒排序（冒泡改进）

  1. /*
  2. 鸡尾酒排序算法，冒泡排序算法的改进版本，
  3. 从左至右，先将最大元素放到最后，然后从右至左，把最小的元素放到前面
  4. */
  5. void cockTailSort(int arr[], int n)
  6. {
  7.     int left = 0;
  8.     int right = n - 1;
  9.     while (left < right)
  10.     {
  11.         for (int i = left; i < right; i++)
  12.         {
  13.             if (arr[i] > arr[i + 1])
  14.             {
  15.                 swap(arr[i], arr[i + 1]);
  16.             }
  17.         }
  18.         right--;
  19.         for (int j = right; j > left; j--)
  20.         {
  21.             if (arr[j] < arr[j - 1])
  22.             {
  23.                 swap(arr[j], arr[j - 1]);
  24.             }
  25.         }
  26.         left++;
  27.     }
  28. }

2.3 计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

  1. 根据待排序集合中最大元素和最小元素的差值范围，申请额外空间；
  2. 遍历待排序集合，将每一个元素出现的次数记录到元素值对应的额外空间内（最小的数对应的下标为0的位置，语调一个数就给对应的下标处的值+1；
  3. 对额外空间内数据进行计算，得出每一个元素的正确位置；

  4. 将待排序集合每一个元素移动到计算得出的正确位置上。

    1. void countSort(int arr[], int n)
    2. {
    3.  int maxVal = arr[0];
    4.  int minVal = arr[0];
    5.  //找出最大的数跟最小的数，以确定辅助数组的长度
    6.  for (int i = 0; i < n; i++)
    7.  {
    8.      if (arr[i] > maxVal)
    9.      {
    10.          maxVal = arr[i];
    11.      }
    12.      if (arr[i] < minVal)
    13.      {
    14.          minVal = arr[i];
    15.      }
    16.  }
    18.  int arrSize = maxVal - minVal + 1;
    19.  int* countArr = new int[arrSize];
    20.  std::memset(countArr, 0, arrSize * sizeof(int));
    21.  for (int i = 0; i < n; i++)
    22.  {
    23.      countArr[arr[i] - minVal]++; //arr[i] - min 对应辅助数组空间的下标i,在此统计出了arr[i]出现的次数
    24.  }
    25.  int index = 0;
    26.  for (int i = 0; i < arrSize; i++) //countArr[i] 代表（i + minVal）出现的次数
    27.  {
    28.      while (countArr[i]--)
    29.      {
    30.          arr[index++] = i + minVal;//有多少个，就依次往后排
    31.      }
    32.  }
    33.  delete[] countArr;
    34. }

    2.4 堆排序

    堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

  5. 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；

  6. 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
  7. 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。 ```cpp void heapify(int arr[], int i, int n) { int lChild = 2 i + 1; int rChild = 2 i + 2; int maxIndex = i; if (lChild < n && arr[lChild] > arr[maxIndex]) {
    1.  maxIndex = lChild;
    } if (rChild < n && arr[rChild] > arr[maxIndex]) {
    1.  maxIndex = rChild;
    } if (maxIndex != i) {
    1.  std::swap(arr[i], arr[maxIndex]);
    2.  heapify(arr, maxIndex, n);
    } } void buildHeap(int arr[], int n) { for (int i = (n - 1) / 2; i >= 0; i—) {
    1.  heapify(arr, i, n);
    } } void heapSort(int arr[], int n) { buildHeap(arr, n); int heapSize = n; while (heapSize > 1) {
    1.  std::swap(arr[0], arr[heapSize - 1]);
    2.  heapSize--;
    3.  heapify(arr, 0, heapSize);
    }

}

  1. 最佳情况：T(n)  = O(nlogn) 最差情况：T(n) = O(nlogn) 平均情况：T(n) = O(nlogn)
  2. <a name="Ys3YG"></a>
  3. ## 2.5 插入排序
  4. 插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。<br />一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：
  6. 1. 从第一个元素开始，该元素可以认为已经被排序；
  7. 1. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
  8. 1. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
  9. 1. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
  10. 1. 将新元素插入到该位置后；
  11. 1. 重复步骤2~5。
  12. ```cpp
  13. void insertSort(int arr[], int n)
  14. {
  15.     if (n <= 0)
  16.         return;
  17.     int current;
  18.     for (int i = 0; i < n - 1; i++)
  19.     {
  20.         current = arr[i + 1];
  21.         int preIndex = i;
  22.         while (preIndex >= 0 && current < arr[preIndex])
  23.         {
  24.             //将元素逐个向后移动
  25.             arr[preIndex + 1] = arr[preIndex];
  26.             preIndex--;
  27.         }
  28.         //假如比arr[preIndex]大，则应该放preIndex后面，假如是preIndex = -1,此时应该放到0处
  29.         arr[preIndex + 1] = current;
  30.     }
  31.     return;
  32. }

最佳情况：当数组是有序的时候，T(n) = O(n) 最坏情况：当数组是逆序的时候T(n) = O(n2) 平均情况：T(n) = O(n2)

2.6 归并排序

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(nlogn）的时间复杂度。代价是需要额外的内存空间。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

  1. 把长度为n的输入序列分成两个长度为n/2的子序列；
  2. 对这两个子序列分别采用归并排序；

  3. 将两个排序好的子序列合并成一个最终的排序序列。 ```cpp void merge(int arr[], int left, int mid, int r) { //定义一个临时数组，保存排序后的数组 int arrTemp = new int[r - left + 1]; //memset(arrTemp, 0, (r - left + 1) 4);

    int i = left; int j = mid + 1; int index = 0; while (i <= mid && j <= r) {

    1.  if (arr[i] <= arr[j])
    2.  {
    3.      arrTemp[index++] = arr[i++];
    4.  }
    5.  else
    6.  {
    7.      arrTemp[index++] = arr[j++];
    8.  }

    } //左侧的没有比较完 while (i <= mid) {

    1.  arrTemp[index++] = arr[i++];

    } //右侧的没有比较完 while (j <= r) {

    1.  arrTemp[index++] = arr[j++];

    } index = 0; while (left <= r) {

    1.  arr[left++] = arrTemp[index++];

    } delete[] arrTemp; return; }

void split(int arr[], int left, int r) { if (left >= r) return; int mid = (r + left) / 2; split(arr, left, mid); split(arr, mid + 1, r); merge(arr, left, mid, r); } void mergeSort(int arr[], int n) { split(arr, 0, n - 1); return; }

  1. 最佳情况：T(n)  = O(n)  最差情况：T(n) = O(nlogn)  平均情况：T(n) = O(nlogn)
  2. <a name="T4Ilz"></a>
  3. ## 2.7 快速排序
  4. 快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。<br />快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：
  6. 1. 从数列中挑出一个元素，称为 “基准”（pivot）；
  7. 1. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  8. 1. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
  9. ```cpp
  10. void partitionSort(int arr[], int l, int r)
  11. {
  12.     if (l >= r)
  13.         return;
  14.     //为了避免有序数组退化为O(n2)的时间复杂度，首先随机选择一个数据作为基准数据
  15.     srand(time(NULL));
  16.     swap(arr[l], arr[rand() % (r - l + 1) + l]);//随机数在l...r之间
  17.     int i = l;
  18.     int j = r;
  19.     int baseValue = arr[l];//取出基准数据
  20.     while (i < j)
  21.     {
  22.         while (i < j && arr[j] >= baseValue)
  23.         {
  24.             j--;
  25.         }
  26.         if (i < j)
  27.         {
  28.             arr[i] = arr[j];
  29.             i++;
  30.         }
  32.         //从左到右遍历，找到第一个比基数大的数，放到arr[r]的位置
  33.         while (i < j && arr[i] <= baseValue)
  34.         {
  35.             i++;
  36.         }
  37.         if (i < j)
  38.         {
  39.             arr[j] = arr[i];
  40.             j--;
  41.         }
  42.     }
  43.     //此时i == j
  44.     arr[i] = baseValue;
  45.     partitionSort(arr, l, i - 1);
  46.     partitionSort(arr, j + 1, r);
  47. }
  48. void partitionSort3(int arr[], int l, int r)
  49. {
  50.     if (l >= r)
  51.         return;
  52.     //为了避免有序数组退化为O(n2)的时间复杂度，首先随机选择一个数据作为基准数据
  53.     srand(time(NULL));
  54.     swap(arr[l], arr[rand() % (r - l + 1) + l]);//随机数在l...r之间
  55.     int i = l;
  56.     int baseValue = arr[l];//取出基准数据
  57.     int lt = l;     // arr[l+1...lt] < v
  58.     int gt = r + 1; // arr[gt...r] > v
  60.     while (i < gt)
  61.     {
  62.         if (arr[i] < baseValue)
  63.         {
  64.             swap(arr[i], arr[lt + 1]);
  65.             lt++;
  66.             i++;
  67.         }
  68.         else if (arr[i] > baseValue)
  69.         {
  70.             swap(arr[gt - 1], arr[i]);
  71.             gt--;
  72.             //此时i不可++，因为后面的元素并没有保存下来，需要下一轮进行判定
  73.         }
  74.         else
  75.         {
  76.             i++;
  77.         }
  79.     }
  80.     swap(arr[l], arr[lt]);
  82.     partitionSort3(arr, l, lt - 1);
  83.     partitionSort3(arr, gt, r);
  85. }
  86. void quickSort(int arr[], int n)
  87. {
  88.     partitionSort(arr, 0, n - 1);
  89. }

2.8 选择排序

  1. void selectionSort(int arr[], int n)
  2. {
  3.     for (int i = 0; i < n; i++)
  4.     {
  5.         int minIndex = i;
  6.         for (int j = i + 1; j < n; j++)
  7.         {
  8.             if (arr[j] < arr[minIndex])
  9.             {
  10.                 minIndex = j;
  11.             }
  12.         }
  13.         if (minIndex != i)
  14.         {
  15.             swap(arr[i], arr[minIndex]);
  16.         }
  17.     }
  18. }

2.9 测试函数

  1. namespace SortTestHelper {
  3.     // 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR]
  4.     int* generateRandomArray(int n, int range_l, int range_r) {
  6.         int* arr = new int[n];
  8.         srand(time(NULL));
  9.         for (int i = 0; i < n; i++)
  10.             arr[i] = rand() % (range_r - range_l + 1) + range_l;
  11.         return arr;
  12.     }
  15.     // 生成一个近乎有序的数组
  16.     // 首先生成一个含有[0...n-1]的完全有序数组, 之后随机交换swapTimes对数据
  17.     // swapTimes定义了数组的无序程度:
  18.     // swapTimes == 0 时, 数组完全有序
  19.     // swapTimes 越大, 数组越趋向于无序
  20.     int* generateNearlyOrderedArray(int n, int swapTimes) {
  22.         int* arr = new int[n];
  23.         for (int i = 0; i < n; i++)
  24.             arr[i] = i;
  26.         srand(time(NULL));
  27.         for (int i = 0; i < swapTimes; i++) {
  28.             int posx = rand() % n;
  29.             int posy = rand() % n;
  30.             swap(arr[posx], arr[posy]);
  31.         }
  33.         return arr;
  34.     }
  35.     //// 拷贝整型数组a中的所有元素到一个新的数组, 并返回新的数组
  36.     //int* copyIntArray(int a[], int n)
  37.     //{
  38.     //    int* arr = new int[n];
  39.     //    //在VS中, copy函数被认为是不安全的, 请大家手动写一遍for循环
  40.     //    copy(a, a + n, arr);
  41.     //    return arr;
  42.     //}
  44.     // 打印arr数组的所有内容
  45.     template<typename T>
  46.     void printArray(T arr[], int n) {
  48.         for (int i = 0; i < n; i++)
  49.             cout << arr[i] << " ";
  50.         cout << endl;
  52.         return;
  53.     }
  55.     // 判断arr数组是否有序
  56.     template<typename T>
  57.     bool isSorted(T arr[], int n) {
  59.         for (int i = 0; i < n - 1; i++)
  60.             if (arr[i] > arr[i + 1])
  61.                 return false;
  63.         return true;
  64.     }
  66.     // 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间
  67.     template<typename T>
  68.     void testSort(const string& sortName, void (*sort)(T[], int), T arr[], int n) {
  70.         clock_t startTime = clock();
  71.         sort(arr, n);
  72.         clock_t endTime = clock();
  73.         cout << sortName << " : " << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
  75.         assert(isSorted(arr, n));
  77.         return;
  78.     }
  80. };