与树的遍历类似,图的遍历就是从图的某一点出发,按照某搜索方式对图中的所有节点都仅访问一次。图的遍历根据搜索方式不同,分为广度优先遍历和深度优先遍历。
广度优先遍历(Breadth First Search,BFS)
广度遍历也就是宽度优先遍历,指从某个点出发,一次性访问所有未被访问的邻接点,再依次从这些已经访问过的邻接点出发,一层一层的访问。他的特点就是先被访问的节点,其邻接点先被访问。
由他的特点可以想到,先来先搜索,显然可借助队列特性。又因为每个节点只访问一次,所以设置一个辅助数组visit【】,初值为FALSE,访问后该节点标为TRUE。
算法步骤
- 初始化所有节点均未被访问,并初始化一个空队列。
- 从图中某个节点v出发,访问v并标记为已被访问,将v入队。
- 若队列非空,则继续执行,否则算法结束。
- 将队头元素v出队,依次访问v的所有未被访问的邻接点,标记已被访问并入队,转向步骤3.
图解见视频。
广度优先遍历经过的节点和边,被称作广度优先生成树,若广度优先遍历非连通图,则每个连通分量都会产生一棵广度优先生成树。
算法实现:
基于邻接矩阵实现的广度优先遍历
#include<iostream>#include<queue>//引入队列头文件using namespace std;const int MaxVnum=100;//顶点数最大值bool visited[MaxVnum]; //访问标志数组,其初值为"false"typedef char VexType; //顶点的数据类型,根据需要定义typedef int EdgeType; //边上权值的数据类型,若不带权值的图,则为0或1typedef struct{VexType Vex[MaxVnum];EdgeType Edge[MaxVnum][MaxVnum];int vexnum,edgenum; //顶点数,边数}AMGraph;int locatevex(AMGraph G,VexType x){for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标if(x==G.Vex[i])return i;return -1;//没找到}void CreateAMGraph(AMGraph &G){//创建有向图的邻接矩阵int i,j;VexType u,v;cout<<"请输入顶点数:"<<endl;cin>>G.vexnum;cout<<"请输入边数:"<<endl;cin>>G.edgenum;cout<<"请输入顶点信息:"<<endl;for(int i=0;i<G.vexnum;i++)//输入顶点信息,存入顶点信息数组cin>>G.Vex[i];for(int i=0;i<G.vexnum;i++)//初始化邻接矩阵所有值为0,如果是网,则初始化邻接矩阵为无穷大for(int j=0;j<G.vexnum;j++)G.Edge[i][j]=0;cout<<"请输入每条边依附的两个顶点:"<<endl;while(G.edgenum--){cin>>u>>v;i=locatevex(G,u);//查找顶点u的存储下标j=locatevex(G,v);//查找顶点v的存储下标if(i!=-1&&j!=-1)G.Edge[i][j]=1; //邻接矩阵储置1,若无向图G.Edge[i][j]=G.Edge[j][i]=1else{cout<<"输入顶点信息错!请重新输入!"<<endl;G.edgenum++;//本次输入不算}}}void print(AMGraph G){//输出邻接矩阵cout<<"图的邻接矩阵为:"<<endl;for(int i=0;i<G.vexnum;i++){for(int j=0;j<G.vexnum;j++)cout<<G.Edge[i][j]<<"\t";cout<<endl;}}void BFS_AM(AMGraph G,int v){//基于邻接矩阵的广度优先遍历int u,w;queue<int>Q; //创建一个普通队列(先进先出),里面存放int类型cout<<G.Vex[v]<<"\t";visited[v]=true;Q.push(v); //源点v入队while(!Q.empty()){ //如果队列不空u=Q.front();//取出队头元素赋值给uQ.pop(); //队头元素出队for(w=0;w<G.vexnum;w++){//依次检查u的所有邻接点if(G.Edge[u][w]&&!visited[w]){//u、w邻接而且w未被访问cout<<G.Vex[w]<<"\t";visited[w]=true;Q.push(w);}}}}int main(){int v;VexType c;AMGraph G;CreateAMGraph(G);print(G);cout << "请输入遍历图的起始点:";cin>>c;v=locatevex(G,c);//查找顶点u的存储下标if(v!=-1){cout<<"广度优先搜索遍历图结果:"<<endl;BFS_AM(G,v);}elsecout<<"输入顶点信息错!请重新输入!"<<endl;return 0;}/*测试数据6 91 2 3 4 5 61 31 22 43 53 24 64 35 65 41*/
基于邻接表的广度优先遍历
#include<iostream>#include<queue>//引入队列头文件using namespace std;const int MaxVnum=100;//顶点数最大值bool visited[MaxVnum]; //访问标志数组,其初值为"false"typedef char VexType;//顶点的数据类型为字符型typedef struct AdjNode{ //定义邻接点类型int v; //邻接点下标struct AdjNode *next; //指向下一个邻接点}AdjNode;typedef struct VexNode{ //定义顶点类型VexType data; // VexType为顶点的数据类型,根据需要定义AdjNode *first; //指向第一个邻接点}VexNode;typedef struct{//定义邻接表类型VexNode Vex[MaxVnum];int vexnum,edgenum; //顶点数,边数}ALGraph;int locatevex(ALGraph G,VexType x){for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标if(x==G.Vex[i].data)return i;return -1;//没找到}void insertedge(ALGraph &G,int i,int j){//插入一条边AdjNode *s;s=new AdjNode;s->v=j;s->next=G.Vex[i].first;G.Vex[i].first=s;}void printg(ALGraph G){//输出邻接表cout<<"----------邻接表如下:----------"<<endl;for(int i=0;i<G.vexnum;i++){AdjNode *t=G.Vex[i].first;cout<<G.Vex[i].data<<": ";while(t!=NULL){cout<<"["<<t->v<<"] ";t=t->next;}cout<<endl;}}void CreateALGraph(ALGraph &G){//创建有向图邻接表int i,j;VexType u,v;cout<<"请输入顶点数和边数:"<<endl;cin>>G.vexnum>>G.edgenum;cout<<"请输入顶点信息:"<<endl;for(i=0;i<G.vexnum;i++)//输入顶点信息,存入顶点信息数组cin>>G.Vex[i].data;for(i=0;i<G.vexnum;i++)G.Vex[i].first=NULL;cout<<"请依次输入每条边的两个顶点u,v"<<endl;while(G.edgenum--){cin>>u>>v;i=locatevex(G,u);//查找顶点u的存储下标j=locatevex(G,v);//查找顶点v的存储下标if(i!=-1&&j!=-1)insertedge(G,i,j);else{cout<<"输入顶点信息错!请重新输入!"<<endl;G.edgenum++;//本次输入不算}}}void BFS_AL(ALGraph G,int v){//基于邻接表的广度优先遍历int u,w;AdjNode *p;queue<int>Q; //创建一个普通队列(先进先出),里面存放int类型cout<<G.Vex[v].data<<"\t";visited[v]=true;Q.push(v); //源点v入队while(!Q.empty()){ //如果队列不空u=Q.front();//取出队头元素赋值给uQ.pop(); //队头元素出队p=G.Vex[u].first;while(p){//依次检查u的所有邻接点w=p->v;//w为u的邻接点if(!visited[w]){//w未被访问cout<<G.Vex[w].data<<"\t";visited[w]=true;Q.push(w);}p=p->next;}}}void BFS_AL(ALGraph G){//非连通图,基于邻接表的广度优先遍历for(int i=0;i<G.vexnum;i++)//非连通图需要查漏点,检查未被访问的顶点if(!visited[i])//i未被访问,以i为起点再次广度优先遍历BFS_AL(G,i);}int main(){ALGraph G;int v;VexType c;CreateALGraph(G);//创建有向图邻接表printg(G);//输出邻接表cout<<"请输入遍历图的起始点:";cin>>c;v=locatevex(G,c);//查找顶点u的存储下标if(v!=-1){cout<<"广度优先搜索遍历图结果:"<<endl;BFS_AL(G,v);}elsecout<<"输入顶点信息错!请重新输入!"<<endl;return 0;}/*测试数据6 91 2 3 4 5 61 31 22 43 53 24 64 35 65 41*/
深度优先遍历(Depth First Search,DFS)
深度优先搜索,是指沿着一条路径一直搜索下去,在无法搜索时,回退到刚刚访问的节点。深度优先遍历是按照深度优先搜索的方式对图进行遍历的。它的特点就是:后被访问的节点,其邻接点先被访问到。
显然,根据后来者先被搜索的特性,我们需要栈来辅助我们实现。递归本来就是使用栈实现的,因而使用递归的方法更方便。
算法步骤
- 初始化图中的所有节点均未被访问
- 从图中的某个节点v出发,访问v并标记
- 依次检查v的邻接点w,若w未被访问,则从w出发进行深度优先遍历(递归调用,重复2,3步)
图解如视频.
基于邻接矩阵实现的深度优先遍历
#include<iostream>
using namespace std;
const int MaxVnum=100; //顶点数最大值
bool visited[MaxVnum]; //访问标志数组,其初值为"false"
typedef char VexType; //顶点的数据类型,根据需要定义
typedef int EdgeType; //边上权值的数据类型,若不带权值的图,则为0或1
typedef struct{
VexType Vex[MaxVnum];
EdgeType Edge[MaxVnum][MaxVnum];
int vexnum,edgenum; //顶点数,边数
}AMGraph;
int locatevex(AMGraph G,VexType x){
for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
if(x==G.Vex[i])
return i;
return -1;//没找到
}
void CreateAMGraph(AMGraph &G){//创建无向图的邻接矩阵
int i,j;
VexType u,v;
cout<<"请输入顶点数:"<<endl;
cin>>G.vexnum;
cout<<"请输入边数:"<<endl;
cin>>G.edgenum;
cout<<"请输入顶点信息:"<<endl;
for(int i=0;i<G.vexnum;i++)//输入顶点信息,存入顶点信息数组
cin>>G.Vex[i];
for(int i=0;i<G.vexnum;i++)//初始化邻接矩阵所有值为0,如果是网,则初始化邻接矩阵为无穷大
for(int j=0;j<G.vexnum;j++)
G.Edge[i][j]=0;
cout<<"请输入每条边依附的两个顶点:"<<endl;
while(G.edgenum--){
cin>>u>>v;
i=locatevex(G,u);//查找顶点u的存储下标
j=locatevex(G,v);//查找顶点v的存储下标
if(i!=-1&&j!=-1)
G.Edge[i][j]=G.Edge[j][i]=1; //若有向图G.Edge[i][j]=1
else{
cout<<"输入顶点信息错!请重新输入!"<<endl;
G.edgenum++;//本次输入不算
}
}
}
void print(AMGraph G){//输出邻接矩阵
cout<<"图的邻接矩阵为:"<<endl;
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++)
cout<<G.Edge[i][j]<<"\t";
cout<<endl;
}
}
void DFS_AM(AMGraph G,int v){//基于邻接矩阵的深度优先遍历
int w;
cout<<G.Vex[v]<<"\t";
visited[v]=true;
for(w=0;w<G.vexnum;w++)//依次检查v的所有邻接点
if(G.Edge[v][w]&&!visited[w])//v、w邻接而且w未被访问
DFS_AM(G,w);//从w顶点开始递归深度优先遍历
}
int main(){
int v;
VexType c;
AMGraph G;
CreateAMGraph(G);//创建无向图的邻接矩阵
print(G);
cout<<"请输入遍历连通图的起始点:";
cin>>c;
v=locatevex(G,c);//查找顶点u的存储下标
if(v!=-1){
cout<<"深度优先搜索遍历连通图结果:"<<endl;
DFS_AM(G,v);
}
else
cout<<"输入顶点信息错!请重新输入!"<<endl;
return 0;
}
/*测试数据
8 9
1 2 3 4 5 6 7 8
1 3
1 2
2 6
2 5
2 4
3 8
3 7
4 5
7 8
1
*/
基于邻接表实现的深度优先遍历
#include<iostream>
using namespace std;
const int MaxVnum=100; //顶点数最大值
bool visited[MaxVnum]; //访问标志数组,其初值为"false"
typedef char VexType; //顶点的数据类型为字符型
typedef struct AdjNode{ //定义邻接点类型
int v; //邻接点下标
struct AdjNode *next; //指向下一个邻接点
}AdjNode;
typedef struct VexNode{ //定义顶点类型
VexType data; // VexType为顶点的数据类型,根据需要定义
AdjNode *first; //指向第一个邻接点
}VexNode;
typedef struct{//定义邻接表类型
VexNode Vex[MaxVnum];
int vexnum,edgenum; //顶点数,边数
}ALGraph;
int locatevex(ALGraph G,VexType x){
for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
if(x==G.Vex[i].data)
return i;
return -1;//没找到
}
void insertedge(ALGraph &G,int i,int j){//插入一条边
AdjNode *s;
s=new AdjNode;
s->v=j;
s->next=G.Vex[i].first;
G.Vex[i].first=s;
}
void printg(ALGraph G){//输出邻接表
cout<<"----------邻接表如下:----------"<<endl;
for(int i=0;i<G.vexnum;i++){
AdjNode *t=G.Vex[i].first;
cout<<G.Vex[i].data<<": ";
while(t!=NULL){
cout<<"["<<t->v<<"] ";
t=t->next;
}
cout<<endl;
}
}
void CreateALGraph(ALGraph &G){//创建无向图邻接表
int i,j;
VexType u,v;
cout<<"请输入顶点数和边数:"<<endl;
cin>>G.vexnum>>G.edgenum;
cout<<"请输入顶点信息:"<<endl;
for(i=0;i<G.vexnum;i++)//输入顶点信息,存入顶点信息数组
cin>>G.Vex[i].data;
for(i=0;i<G.vexnum;i++)
G.Vex[i].first=NULL;
cout<<"请依次输入每条边的两个顶点u,v"<<endl;
while(G.edgenum--){
cin>>u>>v;
i=locatevex(G,u);//查找顶点u的存储下标
j=locatevex(G,v);//查找顶点v的存储下标
if(i!=-1&&j!=-1){
insertedge(G,i,j);
insertedge(G,j,i);//无向图多插入一条边
}
else{
cout<<"输入顶点信息错!请重新输入!"<<endl;
G.edgenum++;//本次输入不算
}
}
}
void DFS_AL(ALGraph G,int v){//基于邻接表的深度优先遍历
int w;
AdjNode *p;
cout<<G.Vex[v].data<<"\t";
visited[v]=true;
p=G.Vex[v].first;
while(p){//依次检查v的所有邻接点
w=p->v;//w为v的邻接点
if(!visited[w])//w未被访问
DFS_AL(G,w);//从w出发,递归深度优先遍历
p=p->next;
}
}
void DFS_AL(ALGraph G){//非连通图,基于邻接表的深度优先遍历
for(int i=0;i<G.vexnum;i++)//非连通图需要查漏点,检查未被访问的顶点
if(!visited[i])//i未被访问,以i为起点再次深度优先遍历
DFS_AL(G,i);
}
int main(){
ALGraph G;
int v;
VexType c;
CreateALGraph(G);//创建无向图的邻接表
printg(G);//输出邻接表
cout<<"请输入遍历连通图的起始点:";
cin>>c;
v=locatevex(G,c);//查找顶点u的存储下标
if(v!=-1){
cout<<"深度优先搜索遍历连通图结果:"<<endl;
DFS_AL(G,v);
}
else
cout<<"输入顶点信息错!请重新输入!"<<endl;
return 0;
}
/*测试数据
8 9
1 2 3 4 5 6 7 8
1 3
1 2
2 6
2 5
2 4
3 8
3 7
4 5
7 8
1
*/
真题练习
题目描述(蓝桥2017省赛填空题)
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
X 星球的一处迷宫游乐场建在某个小山坡上。它是由 10×1010 \times 1010×10 相互连通的小房间组成的。
房间的地板上写着一个很大的字母。我们假设玩家是面朝上坡的方向站立,则:
- LLL 表示走到左边的房间,
- RRR 表示走到右边的房间,
- UUU 表示走到上坡方向的房间,
- DDD 表示走到下坡方向的房间。
X 星球的居民有点懒,不愿意费力思考。他们更喜欢玩运气类的游戏。这个游戏也是如此!
开始的时候,直升机把 100100100 名玩家放入一个个小房间内。玩家一定要按照地上的字母移动。
迷宫地图如下:
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR
请你计算一下,最后,有多少玩家会走出迷宫,而不是在里边兜圈子?
如果你还没明白游戏规则,可以参看下面一个简化的 4x4 迷宫的解说图:
运行限制
int cnt = 0; int vis[11][11]; char a[11][11];
void dfs(int x,int y) { if(x<1 || y<1 || x>10 || y>10){ cnt++; return ; } if(vis[x][y]) return ; vis[x][y] = true; if(a[x][y] == ‘U’) dfs(x-1,y); if(a[x][y] == ‘D’) dfs(x+1,y); if(a[x][y] == ‘L’) dfs(x,y-1); if(a[x][y] == ‘R’) dfs(x,y+1); }
int main() { fstream f1(“a.txt”); for(int i=1;i<=10;i++) { for(int j=1;j<=10;j++) { f1>>a[i][j]; } } for(int i=1;i<=10;i++) { for(int j=1;j<=10;j++) { for(int t=1;t<=10;t++) { for(int k=1;k<=10;k++) { vis[t][k] = false; } } dfs(i,j); } } cout<<cnt<<endl; return 0; }
<a name="Z44rs"></a>
# 蓝桥杯真题:全球变暖(2018 年省赛)
<a name="fuDyN"></a>
### 题目描述
你有一张某海域 NxNNxNNxN 像素的照片,"."表示海洋、"#"表示陆地,如下所示:<br />.......<br />.##....<br />.##....<br />....##.<br />..####.<br />...###.<br />.......<br />其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。<br />由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。<br />例如上图中的海域未来会变成如下样子:<br />.......<br />.......<br />.......<br />.......<br />....#..<br />.......<br />.......<br />请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
<a name="ZvfJd"></a>
### 输入描述
第一行包含一个整数 N (1≤N≤1000)N\ (1 \leq N \leq 1000)N (1≤N≤1000)。<br />以下 NNN 行 NNN 列代表一张海域照片。<br />照片保证第 1 行、第 1 列、第 NNN 行、第 NNN 列的像素都是海洋。、<br />输出一个整数表示答案。
<a name="lJn4J"></a>
### 输入输出样例
<a name="YzjFr"></a>
#### 示例
输入<br />7 ....... .##.... .##.... ....##. ..####. ...###. ....... <br />输出<br />1
<a name="lV4Xi"></a>
### 运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
```cpp
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int maxn = 1005;
char a[maxn][maxn];
int n;
int vis[maxn][maxn];
int dir[4][2]={{-1,0},{0,-1},{0,1},{1,0}};
struct point
{
int x,y;
point(int _a,int _b)
{
x = _a;
y = _b;
}
};
int bfs(int x,int y)
{
queue<point> q;
q.push(point(x,y));
int left = 0;
while(!q.empty())
{
point p = q.front();
q.pop();
int cnt = 0;
for(int i = 0;i<4;i++)
{
int dx = p.x+dir[i][0],dy = p.y+dir[i][1];
if(dx < 0||dx >= n||dy < 0||dy >= n)
continue;
if(a[dx][dy] == '#')
{
cnt++;
if(!vis[dx][dy])
{
vis[dx][dy]=1;
q.push(point(dx,dy));
}
}
}
if(cnt == 4)
left++;
}
return left;
}
int main()
{
int ans = 0;
scanf("%d", &n);
getchar();
for(int i = 0;i < n;i++)
{
scanf("%s", a[i]);
}
memset(vis, 0, sizeof(vis));
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(a[i][j] == '#' && !vis[i][j])
{
vis[i][j]=1;
if(!bfs(i,j))
ans++;
}
}
}
printf("%d\n", ans);
return 0;
}
题目描述(蓝桥2019 省赛填空)
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
下图给出了一个迷宫的平面图,其中标记为 1 的为障碍,标记为 0 的为可以通行的地方。
010000 000100 001001 110000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这 个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按 DRRURRDDDR 的顺序通过迷宫, 一共 10 步。其中 D、U、L、R分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫(30 行 50 列),请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中 D
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
```cpp
include
include
include
using namespace std; int arr[32][52] = { 0 }; int dir[4][2] = { 1,0,0,-1,0,1,-1,0 }; char ch[4] = { ‘D’,’L’,’R’,’U’ }; int dis[32][52]; bool mark[32][52] = { 0 }; void BFS(int x,int y,int z) { for (int i = 0; i < 4; i++) {
} } bool flag = false; vectorif (arr[x + dir[i][0]][y + dir[i][1]] == 0 && mark[x + dir[i][0]][y + dir[i][1]] == 0) { mark[x + dir[i][0]][y + dir[i][1]] = 1; dis[x + dir[i][0]][y + dir[i][1]] = z + 1; BFS(x + dir[i][0], y + dir[i][1], z + 1); } if (arr[x + dir[i][0]][y + dir[i][1]] == 0 && dis[x + dir[i][0]][y + dir[i][1]] > z+1) { mark[x + dir[i][0]][y + dir[i][1]] = 1; dis[x + dir[i][0]][y + dir[i][1]] = z + 1; BFS(x + dir[i][0], y + dir[i][1], z + 1); }ve; void output() { for (int i = 0; i < ve.size(); i++) {
} cout << endl; } void DFS(int x,int y,int z) { if (x == 30 && y == 50) {cout << ve[i];
} if (flag)return; for (int i = 0; i < 4; i++) {output(); flag = true;
} } int main() { memset(dis, -1, sizeof(dis)); for (int i = 0; i < 32; i++) {if (dis[x + dir[i][0]][y + dir[i][1]] == z+1) { ve.push_back(ch[i]); DFS(x + dir[i][0], y + dir[i][1], z + 1); ve.pop_back(); }
} for (int i = 0; i < 52; i++) {arr[i][0] = 1; mark[i][0] = 1; arr[i][51] = 1; mark[i][51] = 1;
} for (int i = 1; i < 31; i++) {arr[0][i] = 1; mark[0][i] = 1; arr[31][i] = 1; mark[31][i] = 1;
} dis[1][1] = 0; BFS(1, 1, 0); DFS(1,1,0); return 0; }for (int j = 1; j < 51; j++) { arr[i][j] = getchar()-'0'; int r = arr[i][j]; if (arr[i][j] == 1)mark[i][j] = 1; } char h=getchar();
```cpp
#include <iostream>
using namespace std;
int main()
{
cout<<"DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR"<<endl;// 请在此输入您的代码
return 0;
}
题目背景(冬季赛真题)
树的果实
Description
小Y同学是一个高中信息学奥赛里面的蒟蒻,在各位大佬暴切各种dark火题的时候,他还在瑟瑟发抖的学习各种基础知识,在巩固很久的基础知识之后,他终于尝试学习且粗略学懂了他之前一直觉得很高大上的树链剖分,于是他准备尝试去写一写模板题。他点开了做题网站,看到了讨论版一句“萌新学妹刚学oi一个月,树链剖分打错了,求大佬看看”,于是小Y同学立即正义感爆棚点进了这一道题。
题目描述
你梦见了一棵树,这是一棵很茂密的树,因此它有很多的分支。
你注意到这颗树的有 n 个果实,每一棵果实都有自己的编号,且标号为 1 的果实在最上面,像是一个根节点,树上的一个果实 u 到另一个果实 v 的距离,都恰好是一个整数 c ,因为已经固定好了 1 号果实为根节点,所以这棵树的形状已经确定了,你想知道摘下一颗果实,会连带着把它的子树的果实也给摘下来。
而这个摘下来所得到的贡献为(数字出现的次数*数字)的平方
比如2出现了5次,那么贡献即为(25)^2
*数字为两个果实之间的距离即树的边权值,边权值的范围为 c 。
所以你有m组询问,想知道当前询问的果实连带着它的子树果实被摘下来时的贡献是多少。
Input
第1行,三个整数n,m,c分别表示树的大小,询问的个数,边权的范围。(1≤n,m,c≤100000)(1 \leq n,m,c \leq 100000)(1≤n,m,c≤100000)
第2−n行,每行三个整数u,v,vi表示从u到v有一条vi边权的边。
接下来m行,每行一个整数表示询问的节点。
Output
输出m行,每行一个整数代表子树的权值大小。(保证不会超过long long)
Sample Input 1
11 6 10 1 2 9 2 3 1 3 4 6 2 5 7 4 6 5 5 7 7 7 8 8 7 9 3 7 10 6 3 11 3 5 7 10 6 1 5
Sample Output 1
158 109 0 0 547 158
Hint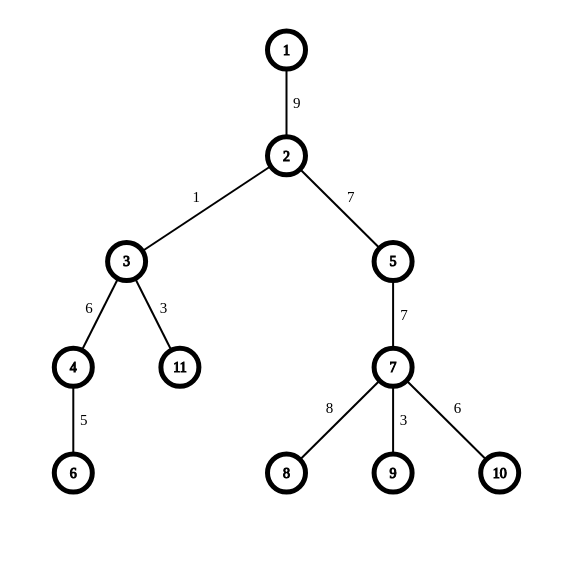
样例如图
对于5节点的子树,贡献为(71)2+(81)2+(31)2+(61)2=158(71)^2+(81)^2+(31)^2+(61)^2=158(71)2+(81)2+(31)2+(61)2=158
对于7节点的子树,贡献为(81)2+(31)2+(6∗1)2=109(81)^2+(31)^2+(61)^2=109(81)2+(31)2+(6∗1)2=109
对于1节点的子树贡献为(32)2+(62)2+(72)2+(51)2+(81)2+(91)2+(1∗1)2=547(32)^2+(62)^2+(72)^2+(51)^2+(81)^2+(91)^2+(11)^2=547(32)2+(62)2+(72)2+(51)2+(81)2+(91)2+(1∗1)2=547
对于6和10节点的子树内没有边,故没有边权做贡献,故贡献为000
#include<bits/stdc++.h>
using namespace std;
#define fo(a,b) for(int i=a;i<=b;i++)
#define ll long long
#define int long long
#define M 400010
#define ll long long
int n,m,k,s=0,v,i,j;
int res=0;
struct Node
{
int id,l,r;
bool operator<(const Node temp)const{
if(l/v==temp.l/v) return r<temp.r;
return l<temp.l;
}
}x[M];
struct node
{
vector<pair<int,int>>v;
}xx[M];
int a[M],ans[M],vis[M];
int in[M],out[M],cnt=0;
void dfs(int d,vector<pair<int,int>>&v,int pre)
{
int l=v.size();
in[d]=++cnt;
a[cnt]=v[i].second;
for(int i=0;i<l;i++){
if(v[i].first!=pre){
dfs(v[i].first,xx[v[i].first].v,d);
}
}
out[d]=cnt;
}
void add(int d){
vis[d]++;
res+=d*d*(vis[d]*vis[d]-(vis[d]-1)*(vis[d]-1));
}
void del(int d){
res+=d*d*(-vis[d]*vis[d]+(vis[d]-1)*(vis[d]-1));
vis[d]--;
}
int solve(int l,int r){
while(i<l) del(a[i++]);
while(i>l) add(a[--i]);
while(j<r) add(a[++j]);
while(j>r) del(a[j--]);
return res;
}
signed main()
{
cin>>n>>m>>k;
v=sqrt(n*1.0);
for(int a,b,c,i=1;i<n;i++){
scanf("%lld%lld%lld",&a,&b,&c);
xx[a].v.push_back(make_pair(b,c));
xx[b].v.push_back(make_pair(a,c));
}
dfs(1,xx[1].v,0);
for(int i=1;i<=m;i++){
int temp;
scanf("%lld",&temp);
x[i].l=in[temp]+1;
x[i].r=out[temp];
x[i].id=i;
}
sort(x+1,x+m+1);
i=1,j=0,res=0;
for(int i=1;i<=m;i++) ans[x[i].id]=solve(x[i].l,x[i].r);
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}

