图通常以一个二元组G=表示，V即节点级，E即边集。|V|表示节点元素的个数，即节点数，也叫图G的阶。比如，在n阶图中有n个节点，|E|表示边集中元素的个数，即边数。
若图G中的每条边是没有方向的，则称为无向图；若图G中的每条边都是有方向的，则称为有向图。在无向图中，每条边都是由两个节点组成的无序对，例如节点V1和V3之间的边，记作（v1,v3）或（v3，v1）。在有向图中，有向边又称为弧，每条弧都是由两个节点组成的有序对，例如从节点v1到节点v3的弧，记作，v1被称作弧尾，v3被称为弧头。
节点的度指与该节点相关联的边数，记作TD（v）。

握手定理

所有节点的度数之和等于边数的两倍，即图论基础 - 图1，其中n为节点数，e为边数。
若在计算度数之和时，每计算一度就画一条小短线，则可看出每条边都被计算了两次，如下图所示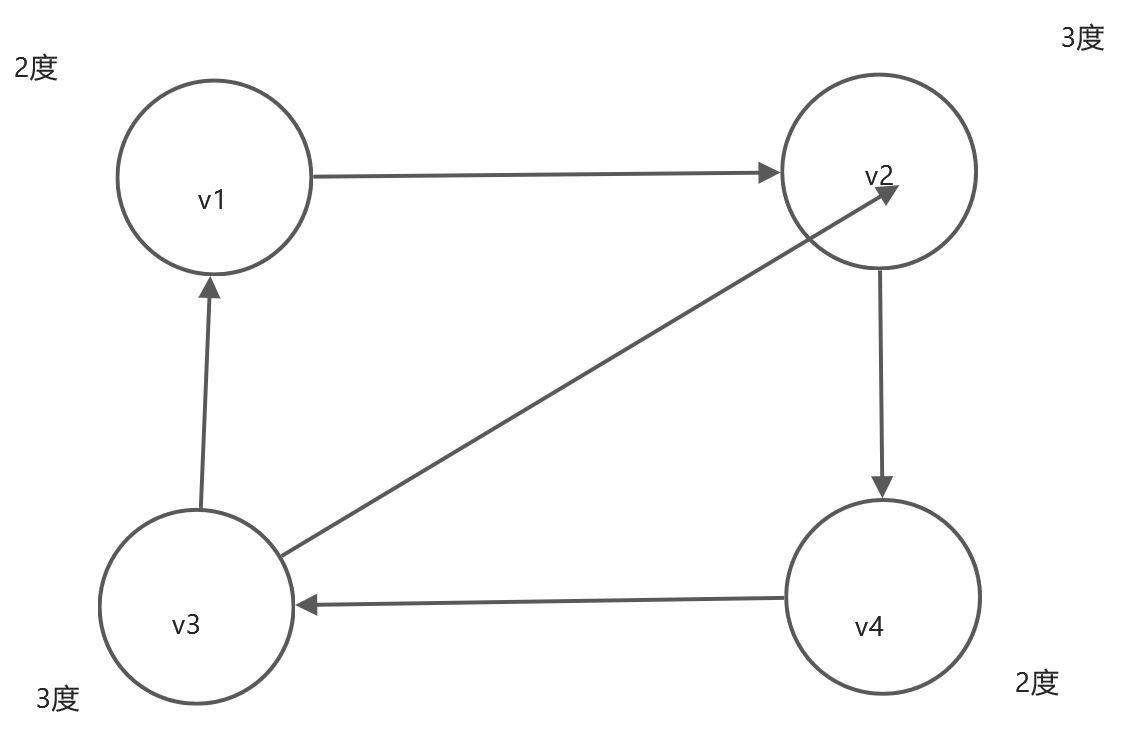
图论基础 - 图2
在有向图中，节点的度又被称为入度和出度。节点v的入度是以节点v为终点的有向边的数量，记作ID（v），即进来的边数，节点v的出度是以节点v为始点的有向边的数量，记作OD（v），即发出的边数。节点v的度等于入度加上出度。所有节点的入度之和等于出度之和，又因为所有节点的度数之和等于边的2倍，因此
图论基础 - 图3

图的存储

图的结构比较复杂，任何两个点之间都可能有关系。图的存储分为顺序存储和链式存储。顺序存储包括邻接矩阵和边集数组，链式存储包括邻接表，链式前向量，十字链表和邻接多重表。

1.邻接矩阵

邻接矩阵一般采用一个一维数组存储图中节点的信息。采用一个二维数组存储图中节点的邻接关系。

表示方法

无向图，有向图和网的邻接矩阵表示方法如下所述。

1.无向图的邻接矩阵

在无向图中，若从节点vi到节点vj有边，则邻接矩阵M[i][j]==M[j][i]=1,否则M[i][j]=0.
特点：
（1）：无向图的邻接矩阵是对称矩阵，且是唯一的。
（2）：第i行或者第j行非零元素的个数正好是第i个节点的度。

2.有向图的邻接矩阵

有向图中，若从vi到vj有边，则邻接矩阵M[i][j]=1,否则M[i][j]=0.
特点：
（1）：有向图的邻接矩阵不一定对称
（2）：第i行非零元素个数正好是第i个元素的出度，第i列非零元素的个数正好是第i+1个节点的入度。

3.网的邻接矩阵

网是带权图，需要存储边的权值，即（见视频）
其中wij表示边上的权值，当i=j时，wii也可被设置为零。

邻接矩阵的数据结构定义

  1. #define MaxVnum 100
  2. typedef char VexType
  3. typedef int EgdeType
  1. Typedef struct{
  2. VexType Vex[MaxVnum];
  3.     EdgeType Edge[MaxVnum][MaxVnum];
  4.     int vexnum,edgenum;
  5. }AMGraph;

邻接矩阵的存储方法

算法步骤：

  1. 输入节点数和边数
  2. 依次输入节点信息，并存储至节点数组Vex[]中
  3. 初始化邻接矩阵，若为图，则初始化为0，若为网，初始化为无穷
  4. 依次输入每条边依附的两个节点，若为网，还需要输入该边的权值。

代码实现如下

  1. #include<iostream>//创建无向图的邻接矩阵
  2. using namespace std;
  3. #define MaxVnum 100  //顶点数最大值
  4. typedef char VexType;  //顶点的数据类型，根据需要定义
  5. typedef int EdgeType;  //边上权值的数据类型，若不带权值的图，则为0或1
  6. typedef struct{
  7.     VexType Vex[MaxVnum];
  8.     EdgeType Edge[MaxVnum][MaxVnum];
  9.     int vexnum,edgenum; //顶点数，边数
  10. }AMGraph;
  12. int locatevex(AMGraph G,VexType x){
  13.     for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
  14.         if(x==G.Vex[i])
  15.             return i;
  16.     return -1;//没找到
  17. }
  20. void CreateAMGraph(AMGraph &G){
  21.     int i,j;
  22.     VexType u,v;
  23.     cout<<"请输入顶点数："<<endl;
  24.     cin>>G.vexnum;
  25.     cout<<"请输入边数:"<<endl;
  26.     cin>>G.edgenum;
  27.     cout<<"请输入顶点信息:"<<endl;
  28.     for(int i=0;i<G.vexnum;i++)//输入顶点信息，存入顶点信息数组
  29.         cin>>G.Vex[i];
  30.     for(int i=0;i<G.vexnum;i++)//初始化邻接矩阵所有值为0，如果是网，则初始化邻接矩阵为无穷大
  31.         for(int j=0;j<G.vexnum;j++)
  32.             G.Edge[i][j]=0;
  33.     cout<<"请输入每条边依附的两个顶点："<<endl;
  34.     while(G.edgenum--){
  35.         cin>>u>>v;
  36.         i=locatevex(G,u);//查找顶点u的存储下标
  37.         j=locatevex(G,v);//查找顶点v的存储下标
  38.         if(i!=-1&&j!=-1)
  39.             G.Edge[i][j]=G.Edge[j][i]=1; //邻接矩阵储置1
  40.         else{
  41.             cout << "输入顶点信息错！请重新输入！"<<endl;
  42.             G.edgenum++;//本次输入不算
  43.         }
  44.     }
  45. }
  47. void print(AMGraph G){//输出邻接矩阵
  48.     cout<<"图的邻接矩阵为："<<endl;
  49.     for(int i=0;i<G.vexnum;i++){
  50.         for(int j=0;j<G.vexnum;j++)
  51.             cout<<G.Edge[i][j]<<"\t";
  52.         cout<<endl;
  53.     }
  54. }
  56. int main(){
  57.     AMGraph G;
  58.     CreateAMGraph(G);
  59.     print(G);
  60.     return 0;
  61. }
  62. /*
  63. 4 5
  64. a b c d
  65. a b
  66. a d
  67. b c
  68. b d
  69. c d
  70. */

邻接矩阵的优缺点：

1.优点是可以快速判断两节点是否有边，方便计算各节点的度，时间复杂度低。
2.缺点是不便于增删节点，不便于访问所有邻接点，空间复杂度高。

边集数组

边集数组通过数组存储每条边的起点和终点，若为网，则增加一个权值域。网的边集数组数据结构定义如下：

  1. struct Edge{
  2. int u;
  3. int v;
  4. int w;
  5. }e[N*N];

采用边集数组计算节点的度或者查找边时，要遍历整个边集数组，时间复杂度为O(e)。除非特殊需要，很少使用边集数组，比如求解最小生成树的kruskal算法时需要按照权值对边进行排序，使用边集数组更方便。

1.邻接表

无向图的邻接表，一个节点的所有邻接点构成一个单链表。
特点：若无向图有n个节点，e条边，则节点表有n个节点，邻接点表有2e个节点。节点的度为该节点后面单链表的节点数。
有向图的邻接表
特点：若有向图有n个节点，e条边，则节点表有n个节点，邻接点表有e个节点。节点的出度为该节点后面单链表中的节点数。
有向图的逆邻接表
特点：若有向图有n个节点，e条边，则节点表有n个节点，邻接点表有e个节点。节点的入度为该节点后面单链表中的节点数。

邻接表数据结构定义

  1. typedef struct VexNode{ 
  2.     VexType data; 
  3.     AdjNode *first; 
  4. }VexNode;
  6. typedef struct{
  7.     VexNode Vex[MaxVnum];
  8.     int vexnum,edgenum; 
  9. }ALGraph;

邻接表存储方法

算法步骤：

  1. 输入节点数和边数
  2. 依次输入节点信息，并存储至节点数组Vex[]的data域中，将first域置空
  3. 依次输入每条边依附的两个节点，若为网，还需要输入该边的权值

实现代码如下

  1. #include<iostream>//创建有向图的邻接表
  2. using namespace std;
  3. const int MaxVnum=100;//顶点数最大值
  4. typedef char VexType;//顶点的数据类型为字符型
  6. typedef struct AdjNode{ //定义邻接点类型
  7.     int v; //邻接点下标
  8.     struct AdjNode *next; //指向下一个邻接点
  9. }AdjNode;
  11. typedef struct VexNode{ //定义顶点类型
  12.     VexType data; // VexType为顶点的数据类型，根据需要定义
  13.     AdjNode *first; //指向第一个邻接点
  14. }VexNode;
  16. typedef struct{//定义邻接表类型
  17.     VexNode Vex[MaxVnum];
  18.     int vexnum,edgenum; //顶点数，边数
  19. }ALGraph;
  21. int locatevex(ALGraph G,VexType x){
  22.     for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
  23.         if(x==G.Vex[i].data)
  24.             return i;
  25.     return -1;//没找到
  26. }
  28. void insertedge(ALGraph &G,int i,int j){//插入一条边
  29.     AdjNode *s;
  30.     s=new AdjNode;
  31.     s->v=j;
  32.     s->next=G.Vex[i].first;
  33.     G.Vex[i].first=s;
  34. }
  36. void printg(ALGraph G){//输出邻接表
  37.     cout<<"----------邻接表如下：----------"<<endl;
  38.     for(int i=0;i<G.vexnum;i++){
  39.         AdjNode *t=G.Vex[i].first;
  40.         cout<<G.Vex[i].data<<"：  ";
  41.         while(t!=NULL){
  42.             cout<<"["<<t->v<<"]\t";
  43.             t=t->next;
  44.         }
  45.         cout<<endl;
  46.     }
  47. }
  49. void CreateALGraph(ALGraph &G){//创建有向图邻接表
  50.     int i,j;
  51.     VexType u,v;
  52.     cout<<"请输入顶点数和边数:"<<endl;
  53.     cin>>G.vexnum>>G.edgenum;
  54.     cout<<"请输入顶点信息:"<<endl;
  55.     for(i=0;i<G.vexnum;i++)//输入顶点信息，存入顶点信息数组
  56.         cin>>G.Vex[i].data;
  57.     for(i=0;i<G.vexnum;i++)
  58.         G.Vex[i].first=NULL;
  59.     cout<<"请依次输入每条边的两个顶点u,v"<<endl;
  60.     while(G.edgenum--){
  61.         cin>>u>>v;
  62.         i=locatevex(G,u);//查找顶点u的存储下标
  63.         j=locatevex(G,v);//查找顶点v的存储下标
  64.         if(i!=-1&&j!=-1)
  65.             insertedge(G,i,j);
  66.         else{
  67.             cout<<"输入顶点信息错！请重新输入！"<<endl;
  68.             G.edgenum++;//本次输入不算
  69.         }
  70.     }
  71. }
  73. int main(){
  74.     ALGraph G;
  75.     CreateALGraph(G);//创建有向图邻接表
  76.     printg(G);//输出邻接表
  77.     return 0;
  78. }
  79. /*
  80. 5 7
  81. a b c d e
  82. a b
  83. a c
  84. a e
  85. b c
  86. c d
  87. c e
  88. d e
  89. */

邻接表优缺点

1.优点是便于增删节点，便于访问所有邻接点，空间复杂度低
2.缺点是不便于判断两个节点间是否有边，不便于计算个节点的度。

  1. #include<iostream>
  2. #include<cstring>
  3. using namespace std;
  4. const int maxn=100000+5;
  5. int maxx[maxn],head[maxn];
  6. int n,m,x,y,w,cnt;
  8. struct Edge{
  9.     int to,w,next;
  10. }e[maxn];
  12. void add(int u,int v,int w){
  13.      e[cnt].to=v;
  14.      e[cnt].w=w;
  15.     e[cnt].next=head[u];
  16.     head[u]=cnt++;
  17. } 
  19. void printg(){
  20.     cout<<"----------链式前向星如下：----------"<<endl;
  21.     for(int v=1;v<=n;v++){
  22.         cout<<v<<"：  ";
  23.         for(int i=head[v];~i;i=e[i].next){    //i=-1 I^1
  24.             int v1=e[i].to,w1=e[i].w;
  25.             cout<<"["<<v1<<" "<<w1<<"]\t";
  26.         }
  27.         cout<<endl;
  28.     }
  29. }
  31. int main(){
  32.     cin>>n>>m;
  33.     memset(head,-1,sizeof(head));
  34.     cnt=0;
  35.     for(int i=1;i<=m;i++){
  36.         cin>>x>>y>>w;
  37.         add(x,y,w);//添加边
  38.         add(y,x,w);//添加反向边 
  39.     }
  40.     printg();
  41.     return 0;
  42. }
  43. /*
  44. 4 5
  45. 1 2 5
  46. 1 4 3
  47. 2 3 8
  48. 2 4 12
  49. 3 4 9
  50. */