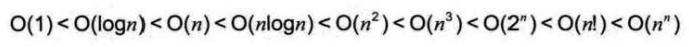算法的时间复杂度定义.

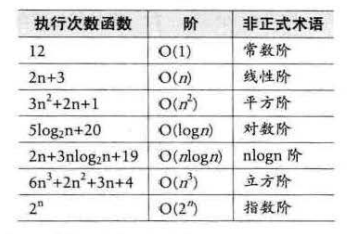
常见的时间复杂度

O(1)—常数阶

单条操作的频度为1，即使他有成千上万条操作，也只是个较大常数，这一类的时间复杂度为O(1)；

temp=a;
a=b;
b=temp;

O(N)—线性阶

第一行频度1，第二行频度为n，第三行频度为n，所以f(n)=n+n+1=2n+1。 根据守则：只要高阶项，不要低阶项目，常数项置为1，去除高阶项的系数：所以时间复杂度O(n)。这一类算法中操作次数和n正比线性增长。

 sum=0；                 
     for(i=0;i<n;i++)       
         sum++；

O(log2N)—对数阶（二分查找）

假设n为100，number是1，小于100退出循环。

• 第1次循环，number = 2，2^1。
• 第2次循环，number = 4, 2^2。
• 第3次循环，number = 8, 2^3。
• 第x次循环，number = 2^x

也就是2^x=n得出x=log₂

int number = 1;//执行1次
int n = 100;//执行1次
while (number < n) {
    number = number * 2; // 执行n/2次
    printf("ssssss");//执行1次
}

O(nlogn)—线性对数阶

数组a和b，a的规模为n，遍历的同时对b进行二分查找

for(int i =0;i<n;i++)
    binary_search(b);
}

O(n^2)—平方阶

int n = 100;
for (int i = 0; i < n; i++) {//执行n次
    for (int j = 0; j < n; j++) {//执行n次
        printf("2222222");
    }
}
for (int i = 0; i < n; i++) {//执行n次
    for (int j = i; j < n; j++) {//执行n - i次
        System.out.println("哈哈");
    }
}

常用的时间复杂度所耗费的时间从小到大依次是：

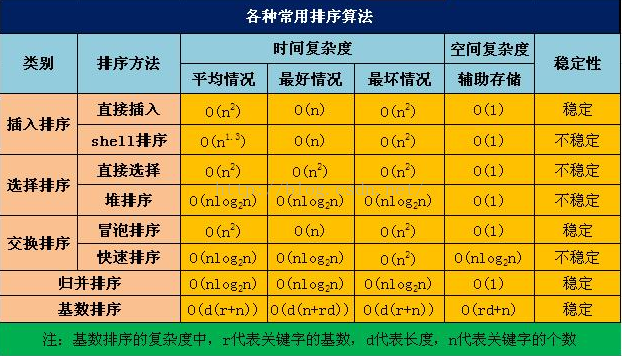
常用算法的时间复杂度和空间复杂度