树

树是一种数据结构，它是由n（n>=0）个有限节点组成一个具有层次关系的集合，把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

  • 每个节点有零个或多个子节点；
  • 没有父节点的节点称为根节点；
  • 每一个非根节点有且只有一个父节点；
  • 除了根节点外，每个子节点可以分为多个不相交的子树。

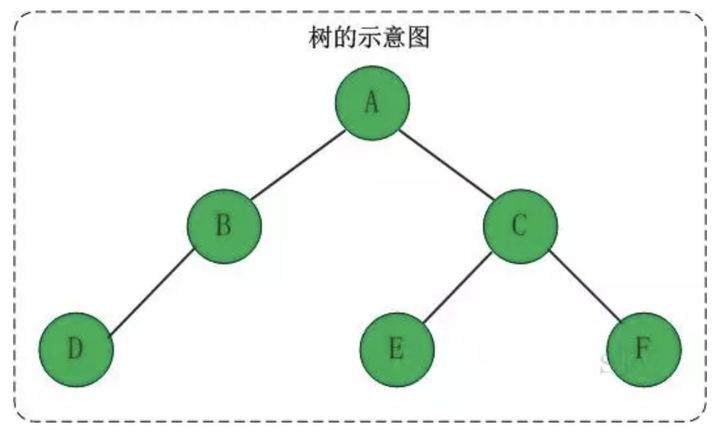
数据结构 - 图1
结点的度：结点拥有的子树的数目，图中结点c的度为2。
叶子：度为零的结点，图中D、E、F都是叶子结点
树的度：树中结点的最大的度，图中结点c的度最大为2，因此树的度为2。节点的度就是节点拥有孩子节点的个数(是孩子不是子孙)。
层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。
树的高度：树中结点的最大层次，图中树的高度为3。
无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。
有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。
相关性质：

  • 树的节点数=所有节点度数+1.
  • 度为m的树第i层最多有m^i-1^个节点。(i>=1)
  • 高度而h的m叉树最多（m^h^-1）/(m-1)个节点(等比数列求和)

  • n个节点的m叉树最小高度[log~m~(n(m-1)+1)]

    二叉搜索树

    定义

    二叉查找树，又被称为二叉搜索树。其特点如下：设x为二叉查找树中的一个结点，x节点包含关键字key，一句话就是左孩子比父节点小，右孩子比父节点大，还有一个特性就是”中序遍历“可以让结点有序。

    作用

  • 查找问题：二分查找

  • 高级结构：字典结构实现
  • 数据变动：节点的插入、删除
  • 遍历问题：前序、中序、后序和层次遍历
  • 数值运算：ceil、floor、找到第 n 大的元素、找到指定元素在排序好的数组的位置 等等

值得一提的是，除了遍历算法，上述各种问题的算法时间复杂度都是 : $O(\log_2 n)$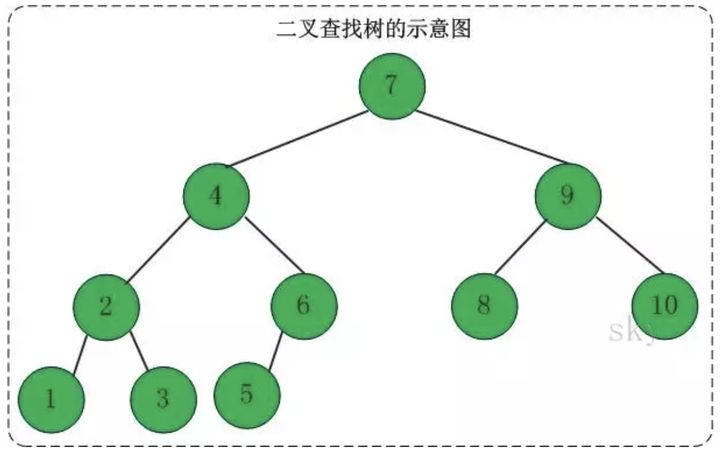
数据结构 - 图2
可以看出，在二叉树中：

  • 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 任意节点的左、右子树也分别为二叉查找树；
  • 没有键值相等的节点。

    插入及查找算法流程

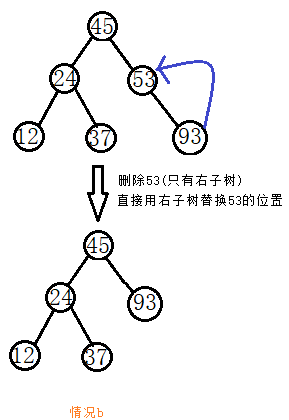
    二叉搜索树的这种特性，使得我们在此二叉树上查找某个值就很方便了，从根节点开始，若要寻找的值小于根节点的值，则在左子树上去找，反之则去右子树查找，知道找到与值相同的节点。
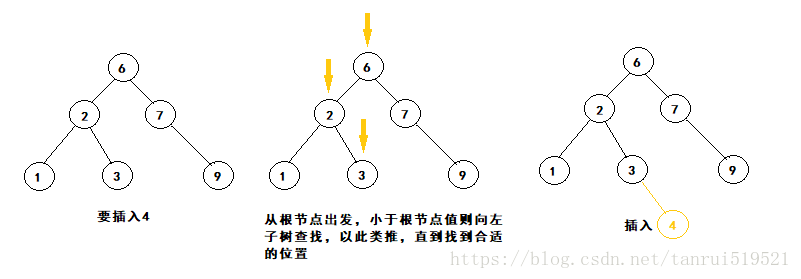
    插入节点也是一样的道理，从根节点出发，所要插入的值，若小于根节点则去左子树寻找该节点所对应的位置，反之去右子树寻找，直到找到该节点合适的位置。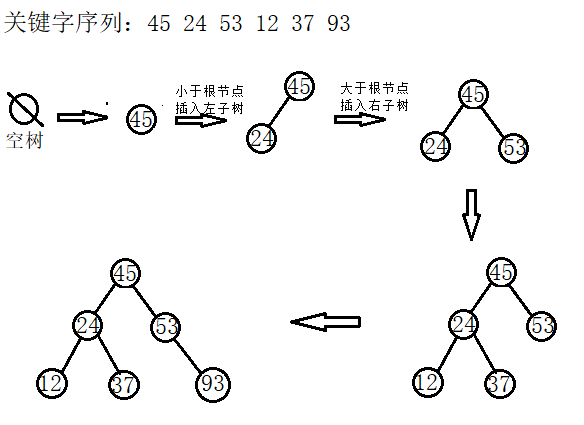
    数据结构 - 图3数据结构 - 图4
    数据结构 - 图5

二叉平衡搜索树（AVL）

数据结构 - 图6

定义

这棵树，说是树，其实它已经退化成链表了，但从概念上来看，它仍是一棵二叉搜索树，只要我们按照逐次增大，如1、2、3、4、5、6的顺序构造一棵二叉搜索树，则形如上图。那么插入的时间复杂度就变成了O(n)，导致这种糟糕的情况原因是因为这棵树极其不平衡，右树的重量远大于左树，因此我们提出了叫平衡二叉搜索树的结构，又称之为AVL树，是因为平衡二叉搜索树的发明者为Adel’son-Vel’skii 和Landis二人。
平衡二叉搜索树，它能保持二叉树的高度平衡，尽量降低二叉树的高度，减少树的平均查找长度。

AVL树的性质

  • 左子树与右子树高度之差的绝对值不超过1
  • 树的每个左子树和右子树都是AVL树

  • 每一个节点都有一个平衡因子（balance factor），任一节点的平衡因子是-1、0、1（每一个节点的平衡因子 = 右子树高度 - 左子树高度）

    插入及查找算法流程

    数据结构 - 图7
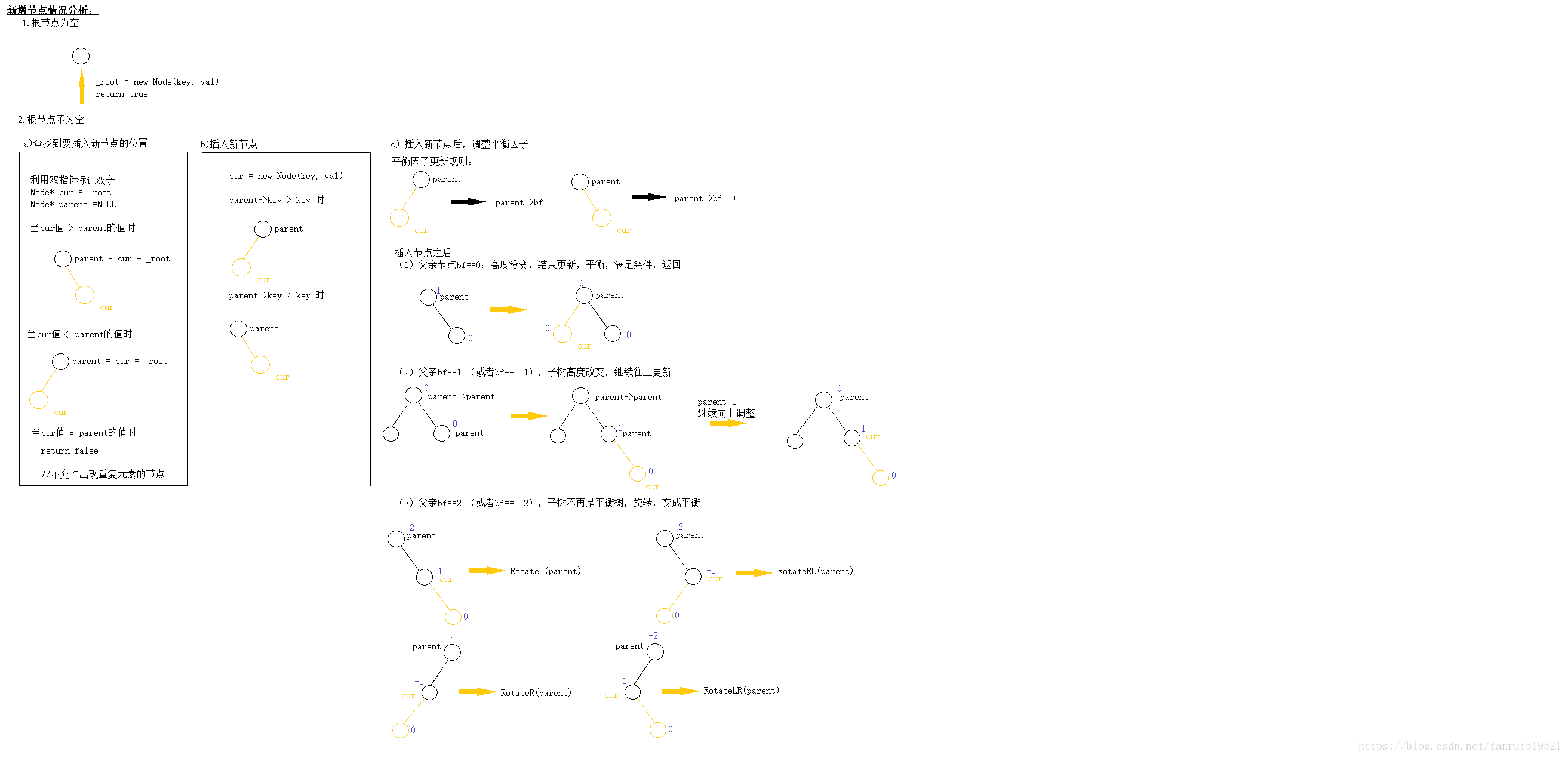
    数据结构 - 图8

    1. template <class K, class V> bool AVLTree<K, V>::AVLInsert(K key, V val) {
    2. // 1.根节点为空，直接插入
    3. if (_root == NULL) {
    4.   _root = new Node(key, val);
    5.   return true;
    6. }
    7. // 2.根节点不为空
    8. else {
    9.   Node *cur = _root;
    10.   Node *parent = NULL;
    11.   // a)找到要插入节点的位置
    12.   while (cur) {
    13.     parent = cur;
    14.     if (cur->_key > key)
    15.       cur = cur->_left;
    16.     else if (cur->_key < key)
    17.       cur = cur->_right;
    18.     else
    19.       return false; //不允许出现重复元素的节点
    20.   }
    21.   // b)插入新节点
    22.   cur = new Node(key, val);
    23.   if (parent->_key > key) {
    24.     parent->_left = cur;
    25.     cur->_parent = parent;
    26.   }
    27.   else {
    28.     parent->_right = cur;
    29.     cur->_parent = parent;
    30.   }
    32.   // c)插入完成后，调整平衡因子
    33.   while (parent) {
    34.     if (cur == parent->_left) //插入节点在左子树父节点bf--，反之++
    35.       parent->_bf--;
    36.     else
    37.       parent->_bf++;
    39.     // 1)插入新节点后，parent->bf==0;说明高度没变，平衡，返回
    40.     if (parent->_bf == 0)
    41.       break;
    42.     // 2)插入节点后parent->_bf==-1||parent->_bf==1;说明子树高度改变，则继续向上调整
    43.     else if (parent->_bf == -1 || parent->_bf == 1) {
    44.       cur = parent;
    45.       parent = parent->_parent;
    46.     }
    47.     // 3)插入节点后parent->_bf==-2||parent->_bf==2；说明已经不平衡，需要旋转
    48.     else {
    49.       if (parent->_bf == 2) {
    50.         if (cur->_bf == 1)
    51.           RotateL(parent);
    52.         else // (cur->_bf == -1)
    53.           RotateRL(parent);
    54.       } else // parent->_bf == -2
    55.       {
    56.         if (cur->_bf == -1)
    57.           RotateR(parent);
    58.         else // (cur->_bf == 1)
    59.           RotateLR(parent);
    60.       }
    61.       break;
    62.     }
    64.   } // end while (parent)
    65.   return true;
    66. }
    67. }