什么是B树
B-tree是一种特殊类型的自平衡搜索树,其中每个节点可以包含多个键,并且可以有两个以上的子节点。它是二叉搜索树的广义形式。 它也被称为高度平衡的多路搜索树。
 |
|---|
| B树 |
为什么需要B树?
随着访问物理存储介质(如硬盘)所需的时间越来越短,B树的需求就出现了。二级存储设备容量较大,但是访问速度较慢,因此需要最小化磁盘的访问。其他数据结构如二叉搜索树、AVL树、红黑树等只能在一个节点中存储一个键。如果你不得不存储大量的key,那么这样的树的高度就会变得非常大,访问时间也会增加。但是B树可以在单个节点中存储多个键,并且可以有多个子节点。这显著降低了高度,允许更快的磁盘访问。
B树属性
- 对于每个节点 ×,key按升序存储。
- 在每个节点中,有一个布尔值用来标识是否是叶子节点。
- 如果 n 是树的顺序,每个内部节点最多可以包含 n - 1 键,以及指向每个子节点的指针。
- 除根之外的每个节点最多可以有 n 个子节点,并且至少有 n/2 子节点。
- 所有叶子都具有相同的深度(即树的高度-h)。
- 根至少有 2 个孩子,并且至少包含 1 个键。
- 如果 n ≥ 1,然后对于任何高度为 h 且最小度数 t ≥ 2 的 n 键 B 树。h ≥ logt (n+1)/2
B树的操作
搜索节点
在B树中搜索元素是在二叉搜索树中搜索元素的一般形式。遵循以下步骤:
- 从根节点开始,将 k 与节点的第一个键进行比较。如果k = 节点中的第一个键,则返回节点和索引。
- 如果k.leaf = true,返回无效的 (即未找到)。
- 如果k < 节点中的第一个键,则递归搜索该键的左子节点。
- 如果当前节点存在多个键,并且 k > 第一个key。则key继续与节点中的下一个键进行比较。否则搜索键的右孩子。
- 重复步骤 1 到 4,直到到达叶子。
搜索示例
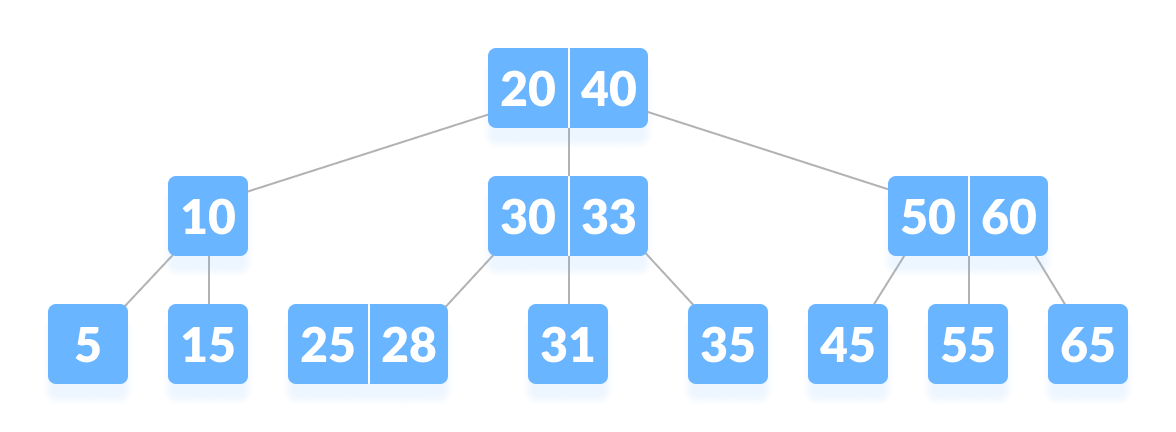
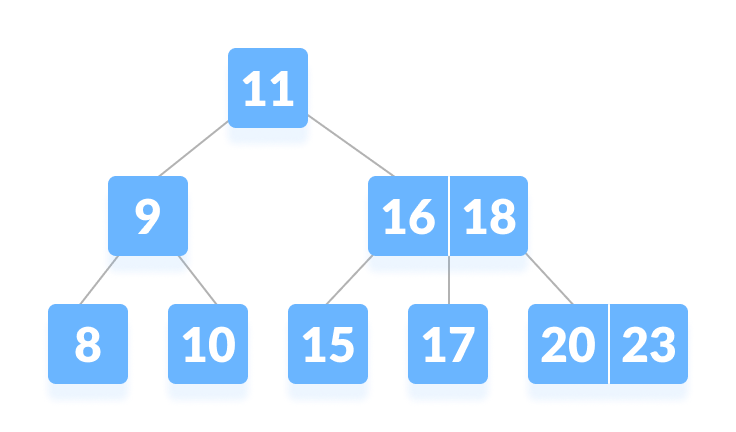
- 用 k = 17的关键字在度数为 3 的的树中搜索。
|
 |
| —- |
| B树 |
|
| —- |
| B树 |
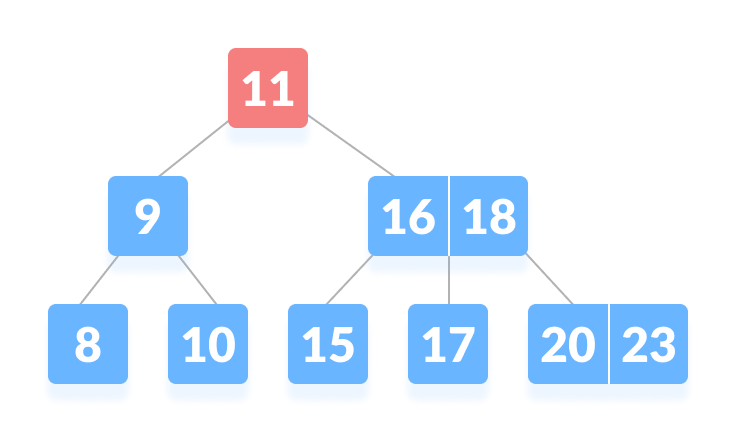
- k 在根节点中找不到。
 |
|---|
| 在根节点上找不到 k |
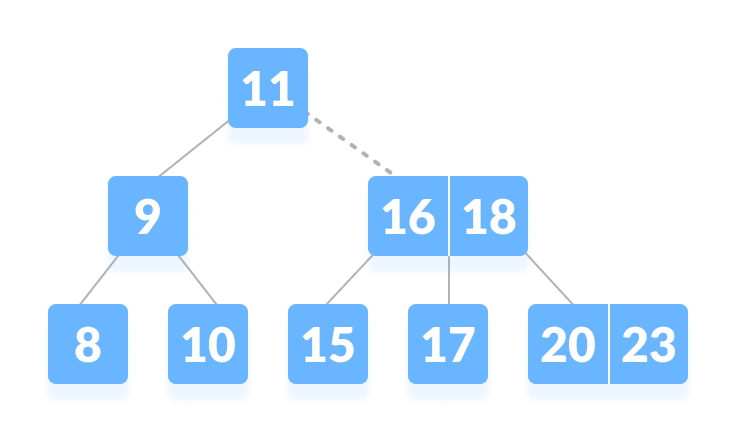
- 由于 k > 11,转到根节点的右子节点。
|
 |
| —- |
| 转到右子树 |
|
| —- |
| 转到右子树 |
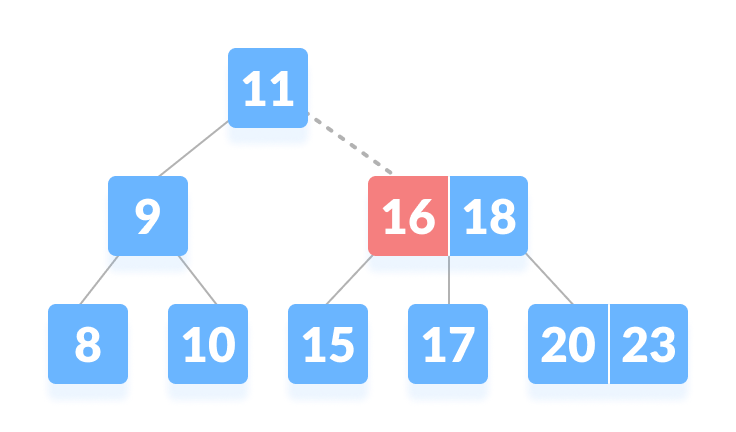
- 将 k与16比较,k>16。将k继续与下一个键18进行比较。
|
 |
| —- |
| 从左到右的对键进行比较 |
|
| —- |
| 从左到右的对键进行比较 |
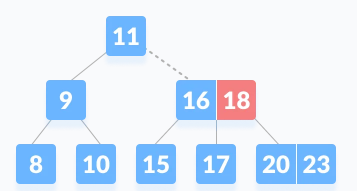
- 由于k<18,k 位于16和18之间。即搜索16的右子节点或18的左子节点。
|
 |
| —- |
| k 介于 16 和 18 之间 |
|
| —- |
| k 介于 16 和 18 之间 |
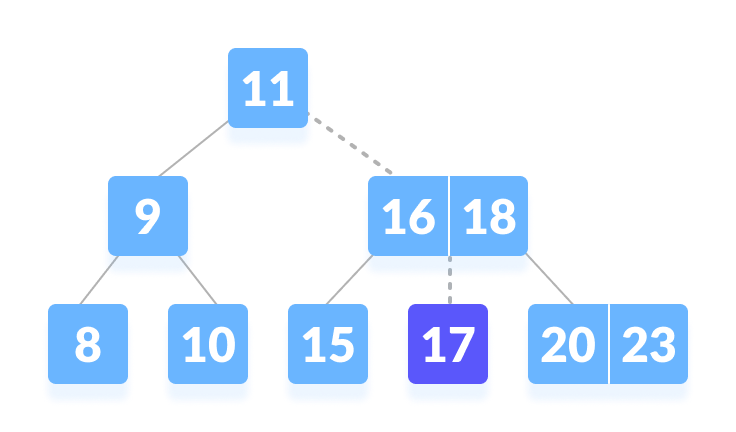
- k 被发现。
|
 |
| —- |
| 找到 k |
|
| —- |
| 找到 k |
插入节点
在B树上插入元素由两个事件组成:**搜索合适的节点**以插入元素并**在需要时拆分节点**。**插入操作始终以自底向上的方式进行。 **
- 如果树为空,则分配一个根节点并插入键。
- 更新节点中的键计数器。
- 搜索合适的节点进行插入。
- 如果节点已满,请按照以下步骤操作。
- 按递增顺序插入元素。
- 如果一个节点的元素数量已经大于它的极限,则会产生节点的分割。
- 将中间键向上推,将左键设为左子键,将右键设为右子键。
- 如果节点未满,请按照以下步骤操作。
- 按递增顺序插入节点。
插入示例
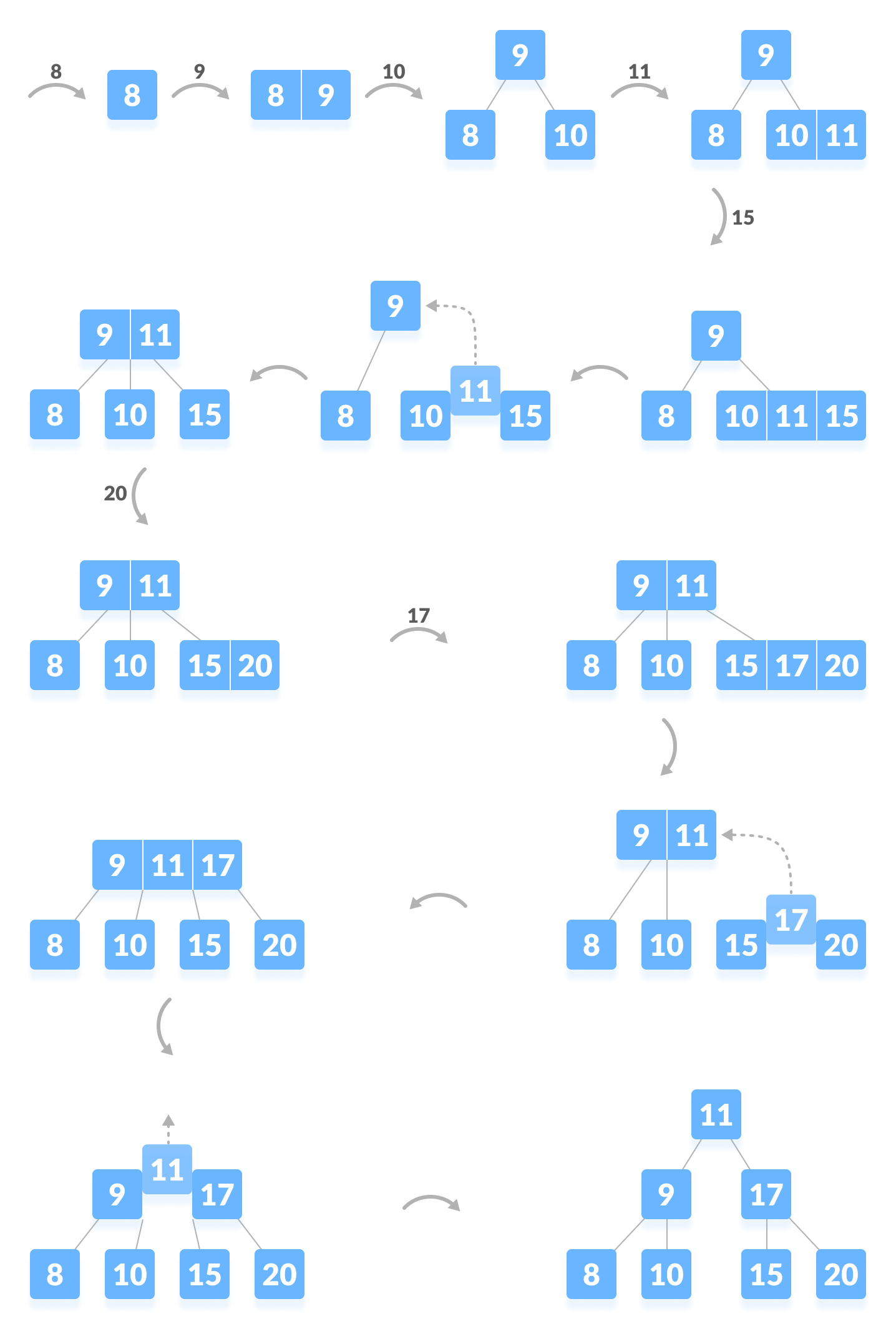
要插入的元素为 8、9、10、11、15、17、18、20、23。
 |
|---|
| 将元素插入到 B 树中 |
删除节点
删除B树上的元素包括三个主要事件:搜索要删除的键所在的节点,删除键并在需要时平衡树。删除时可能会发生称为下溢的情况。当节点包含的键数少于它应该持有的最小数量时,就会发生下溢。
学习删除操作前需要了解的术语有:
- Inorder Predecessor - 节点左子节点上的最大键称为其中序前驱。
- Inorder Successor - 中序后继节点右子节点上的最小键称为其中序后继。
在进行以下步骤之前,必须了解有关度数为 m 的 B树的这些事实。
- 一个节点最多可以有 m 个子节点。(例如:3)
- 一个节点最多可以包含m - 1键。(例如:2)
- 一个节点应该有最少的⌈m/2⌉孩子。(例如:2)
- 一个节点(除了根节点)应该包含最少的⌈m/2⌉ - 1键。(例如:1)
B树中的删除操作主要有3种情况:
案例一:要删除的key在叶子节点
要删除的Key在叶子节点。有两种情况。
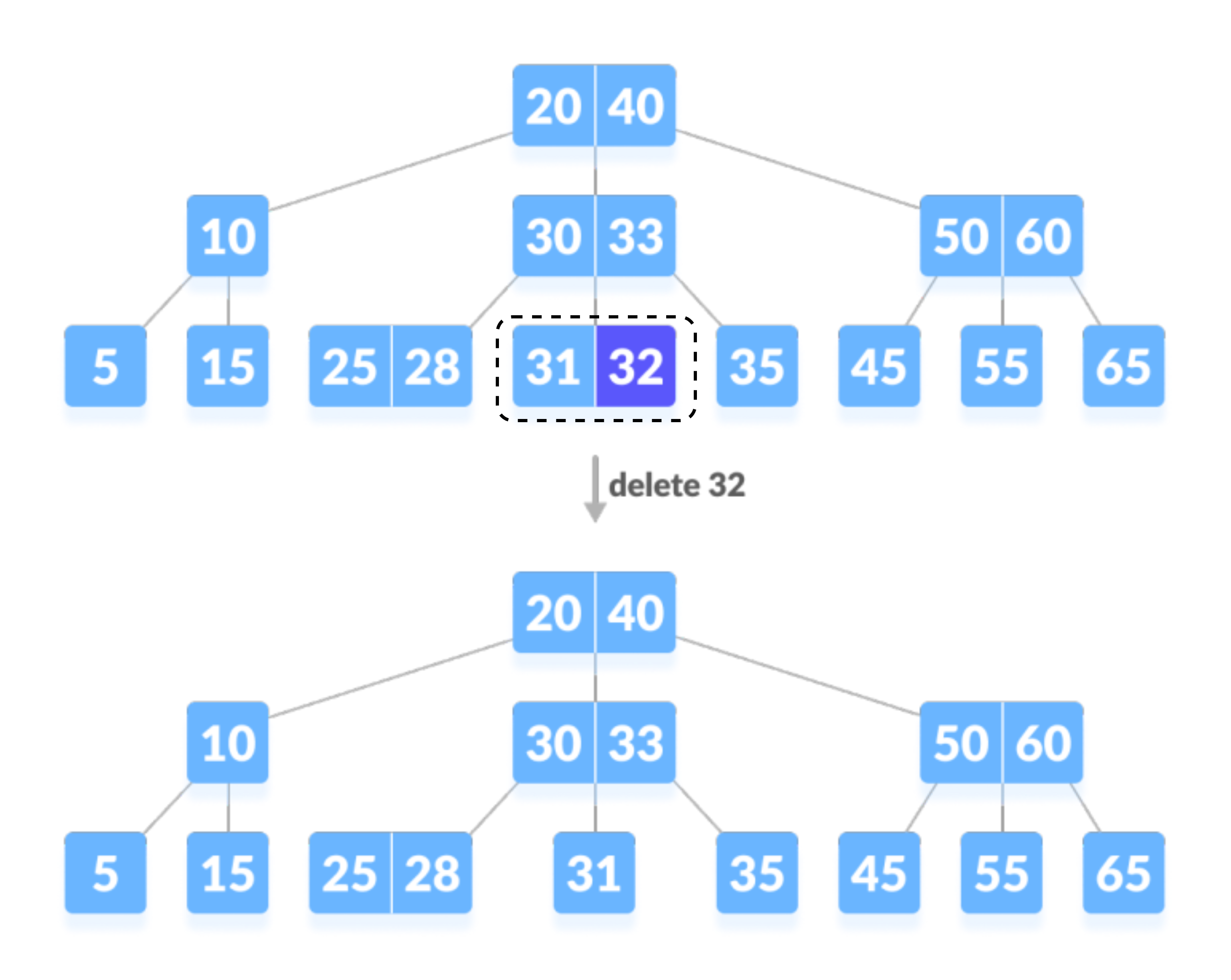
- key的删除不违反节点应满足的最小key数量的约束。在下面的树中,删除 32 并不违反上述属性。
|
 |
| —- |
| 从B树中删除键 (32) |
|
| —- |
| 从B树中删除键 (32) |
删除 key 违反了节点最小key数量的约束。在这种情况下我们按从左到右的顺序从其直接相邻的兄弟节点借用一个键。首先访问紧邻的左兄弟节点。如果左兄弟节点的键数超过最小数量,则从该节点借用一个键。否则,检查以从紧邻的右兄弟节点借用。
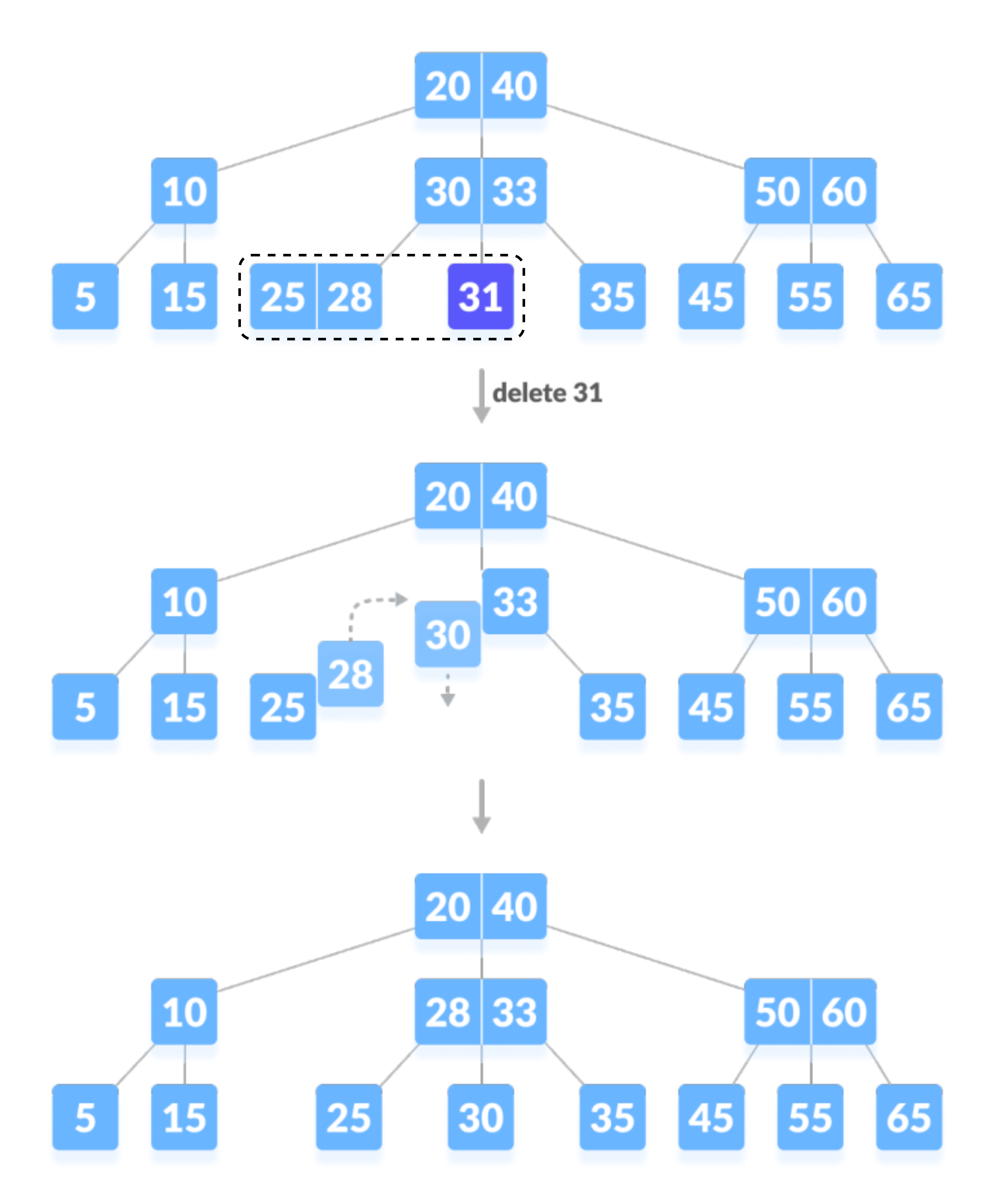
在下面的树中,删除 31 会导致上述情况。让我们从左兄弟节点借一个键。从 B树中删除一个键。
 |
|---|
| 从B树中删除键 (31) |
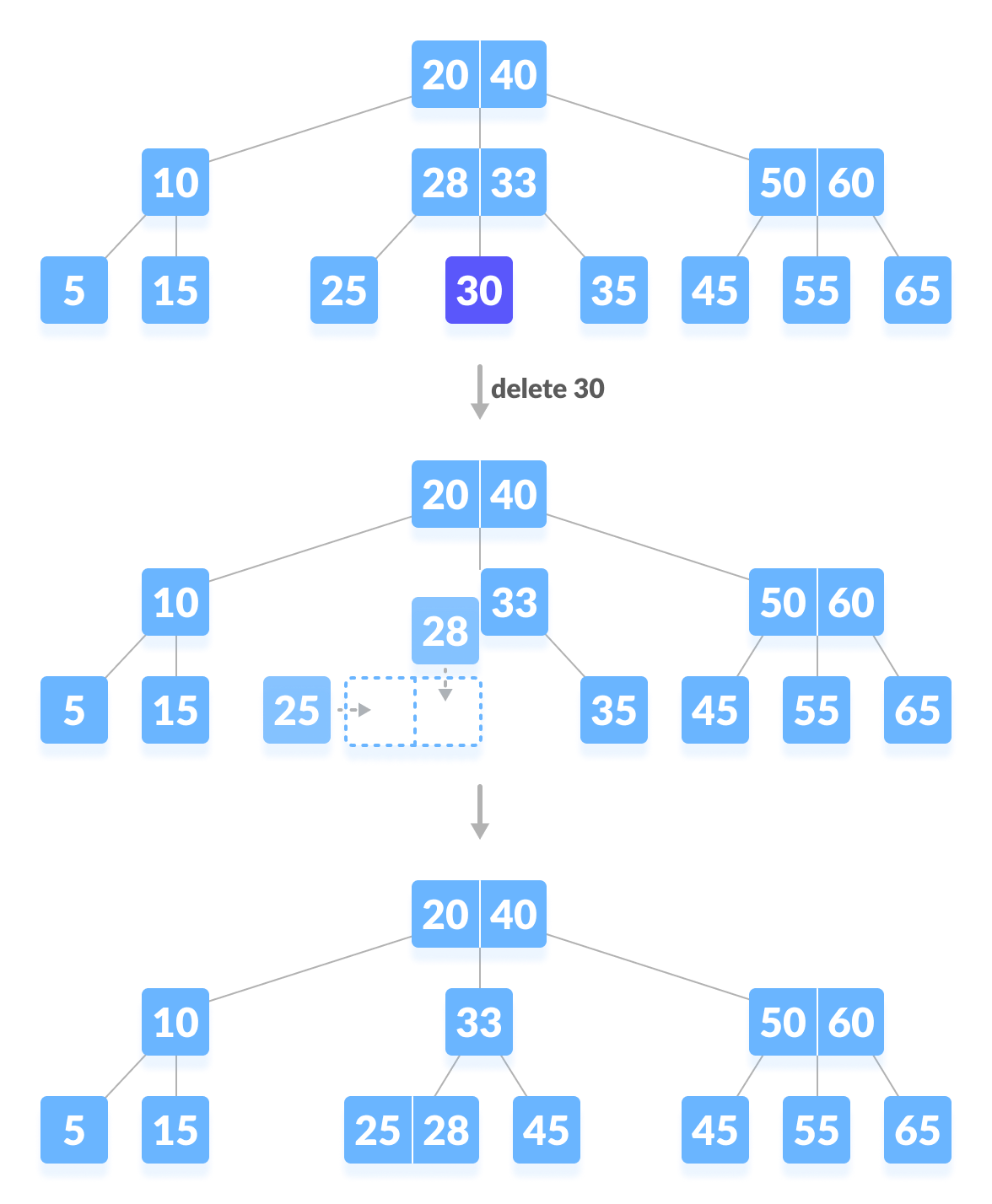
如果两个直接兄弟节点都已经具有最小数量的键,则将该节点与左兄弟节点或右兄弟节点合并。这种合并是通过父节点完成的。
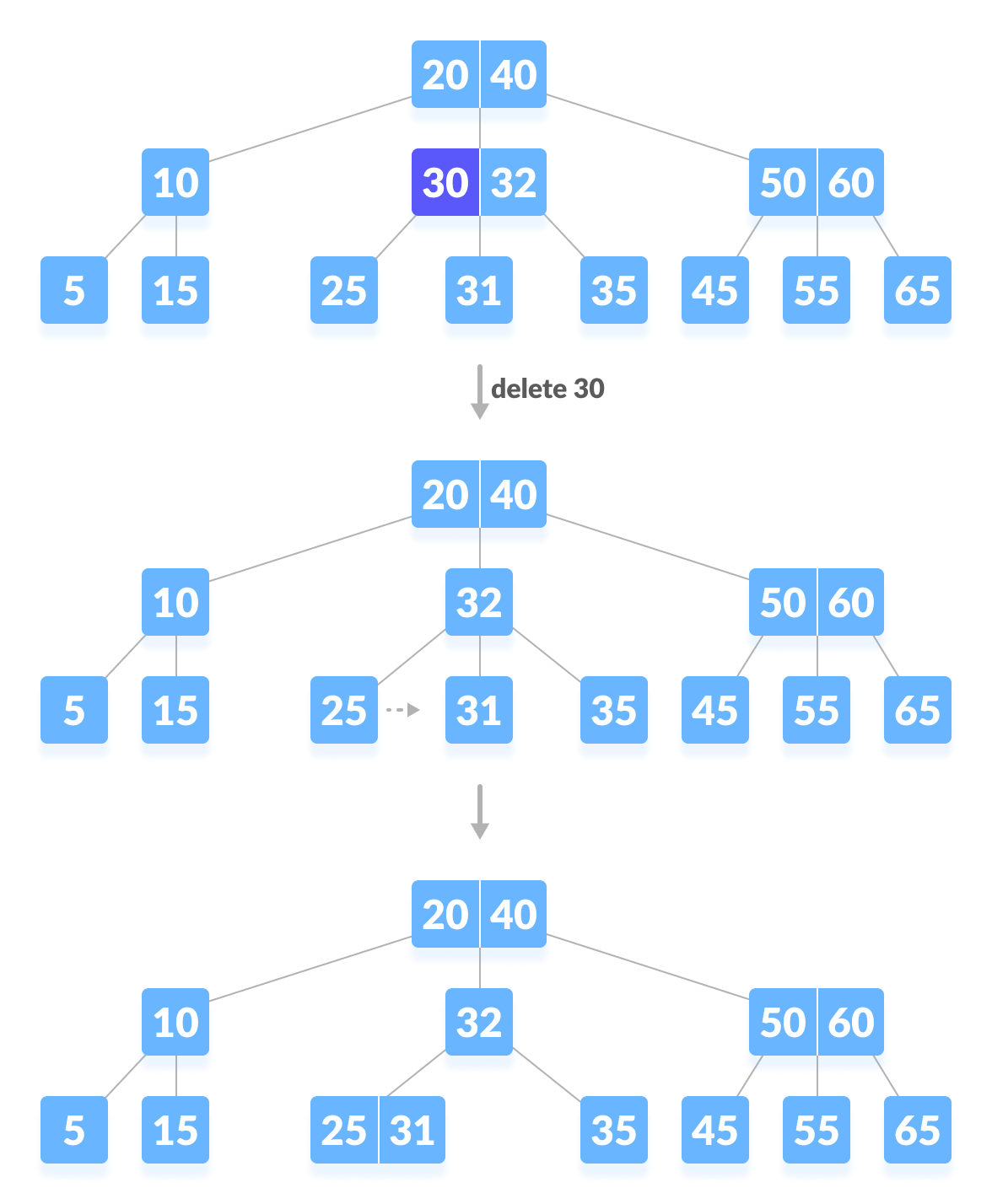
删除 30 会导致上述情况。
 |
|---|
| 从B树中删除键 (30) |
案例二:要删除的key在内部节点
如果要删除的key在内部节点,会出现以下情况。
- 如果该内部节点的左子节点的键数超过最小数量,则被删除的内部节点将被中序前驱替换。或者该内部节点的右子节点的键数超过最小数量,则被删除的内部节点将被中序后继节点替换。
|
 |
| —- |
| 删除内部节点 (33) |
|
| —- |
| 删除内部节点 (33) |
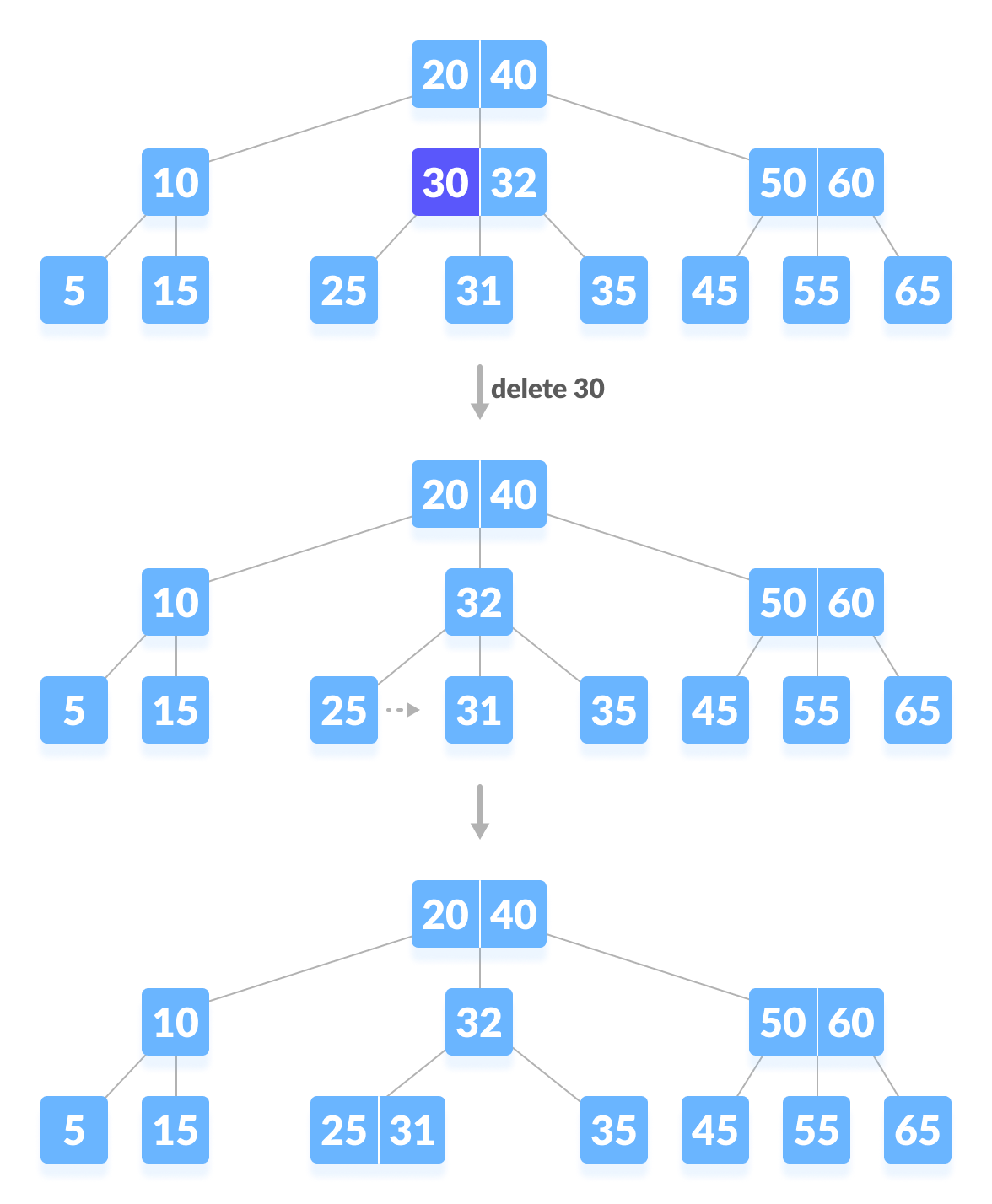
- 如果该内部节点的任何一个孩子的键数正好是最小数量,则合并左孩子和右孩子。
合并后,如果父节点的键数少于最小键数,则在案例一中查找兄弟节点。
 |
|---|
| 删除内部节点 (30) |
案例三
在这种情况下,树的高度会缩小。如果目标键位于内部节点,并且删除键导致节点中键的数量较少(即小于所需的最小值),则查找中序前驱(左子树的最大值)和中序后继(右子树的最小值)。如果两个子节点都包含最少数量的 key,则不能借用。这导致了案例二(3),即合并孩子。再次,寻找兄弟节点借key。但是如果兄弟节点也只有最少数量的键,则将节点与兄弟节点以及父节点合并。相应地排列子节点们(增加顺序)。
 |
|---|
| 删除内部节点(10) |
B树复杂度
搜索复杂度
- 最坏情况时间复杂度: Θ(log n)
- 平均情况时间复杂度: Θ(log n)
- 最佳情况时间复杂度: Θ(log n)
- 平均情况空间复杂度: Θ(n)
- 最坏情况空间复杂度: Θ(n)
删除复杂度
B树的实现
package online.javabook.algo.dsa.api.tree.btree;// Searching a key on a B-tree in Javapublic class BTree {private int degree;/*** Node creation*/public class BTreeNode {// 当前节点存在多少个Keyint keyTotal;// 当前节点包含的keyint keys[] = new int[2 * degree - 1];// 当前节点的子节点容器BTreeNode children[] = new BTreeNode[2 * degree];// 当前节点是否是叶子节点boolean leaf = true;/*** 返回查找的key在当前节点keys容器中的索引位置* @param key* @return*/public int find(int key) {for (int index = 0; index < this.keyTotal; index++) {if (this.keys[index] == key) {return index;}}return -1;}}// btree的根节点private BTreeNode root;/**** @param degree*/public BTree(int degree) {this.degree = degree;this.root = new BTreeNode();this.root.keyTotal = 0;this.root.leaf = true;}/*** 查询key是否存在** @param key* @return*/public boolean contain(int key) {if (this.search(root, key) != null) {return true;} else {return false;}}private BTreeNode search(BTreeNode node, int key) {int keyIndex;// 判断节点的有效性if (node == null)return null;for (keyIndex = 0; keyIndex < node.keyTotal; keyIndex++) {// 如果被查询的key小于当前key列表中的第一个key值,则if (key < node.keys[keyIndex]) {break;}// 如果被查询的key等于当前key列表中的key值,则当前节点就是要找的节点if (key == node.keys[keyIndex]) {return node;}// 否则一直循环递增keyIndex的值,直到返回大于key的结束区间索引位置}if (node.leaf) {return null;} else {return search(node.children[keyIndex], key);}}/*** 插入一个key值,当节点的keys容器满了,则会产生节点的分裂** @param key*/public void insert(final int key) {BTreeNode oldRoot = root;// 如果当前root节点的key已经满了,则创建一个新的BTreeNode节点,并分裂当前节点if (oldRoot.keyTotal == 2 * degree - 1) {BTreeNode newRoot = new BTreeNode();// 用新节点代替root节点root = newRoot;// 新节点为内部节点类型newRoot.leaf = false;// 新节点的keys为空newRoot.keyTotal = 0;// 老的root节点成为新节点的第一个子节点newRoot.children[0] = oldRoot;// 节点分裂split(newRoot, 0, oldRoot);// 将插入的key放入newRoot节点中insertValue(newRoot, key);} else {insertValue(oldRoot, key);}}/*** 节点的分裂** @param newNode* @param pos* @param oldNode*/private void split(BTreeNode newNode, int pos, BTreeNode oldNode) {BTreeNode splitNode = new BTreeNode();splitNode.leaf = oldNode.leaf;splitNode.keyTotal = degree - 1;for (int j = 0; j < degree - 1; j++) {splitNode.keys[j] = oldNode.keys[j + degree];}if (!oldNode.leaf) {for (int j = 0; j < degree; j++) {splitNode.children[j] = oldNode.children[j + degree];}}oldNode.keyTotal = degree - 1;for (int j = newNode.keyTotal; j >= pos + 1; j--) {newNode.children[j + 1] = newNode.children[j];}newNode.children[pos + 1] = splitNode;for (int j = newNode.keyTotal - 1; j >= pos; j--) {newNode.keys[j + 1] = newNode.keys[j];}newNode.keys[pos] = oldNode.keys[degree - 1];newNode.keyTotal = newNode.keyTotal + 1;}/*** Insert the node** @param bTreeNode* @param key*/final private void insertValue(BTreeNode bTreeNode, int key) {if (bTreeNode.leaf) {int i = 0;for (i = bTreeNode.keyTotal - 1; i >= 0 && key < bTreeNode.keys[i]; i--) {bTreeNode.keys[i + 1] = bTreeNode.keys[i];}bTreeNode.keys[i + 1] = key;bTreeNode.keyTotal = bTreeNode.keyTotal + 1;} else {int i = 0;for (i = bTreeNode.keyTotal - 1; i >= 0 && key < bTreeNode.keys[i]; i--) {//}i++;BTreeNode tempNode = bTreeNode.children[i];if (tempNode.keyTotal == 2 * degree - 1) {split(bTreeNode, i, tempNode);if (key > bTreeNode.keys[i]) {i++;}}insertValue(bTreeNode.children[i], key);}}/*** 显示BTree*/public void show() {show(root);}/*** 显示BTree** @param btreeNtode*/private void show(BTreeNode btreeNtode) {for (int i = 0; i < btreeNtode.keyTotal; i++) {System.out.print(btreeNtode.keys[i] + " ");}if (!btreeNtode.leaf) {for (int i = 0; i < btreeNtode.keyTotal + 1; i++) {show(btreeNtode.children[i]);}}}public static void main(String[] args) {BTree bTree = new BTree(3);bTree.insert(8);bTree.insert(9);bTree.insert(10);bTree.insert(11);bTree.insert(15);bTree.insert(20);bTree.insert(17);bTree.show();if (bTree.contain(20)) {System.out.println("\nfound");} else {System.out.println("\nnot found");}}}

