什么是B+树

B+ 树是自平衡树的高级形式，其中所有值都位于叶子节点。 在学习B+树之前要理解的一个重要概念是多级索引。在多级索引中，索引的索引创建如下图。它使访问数据更容易、更快。

B 树 - 图1
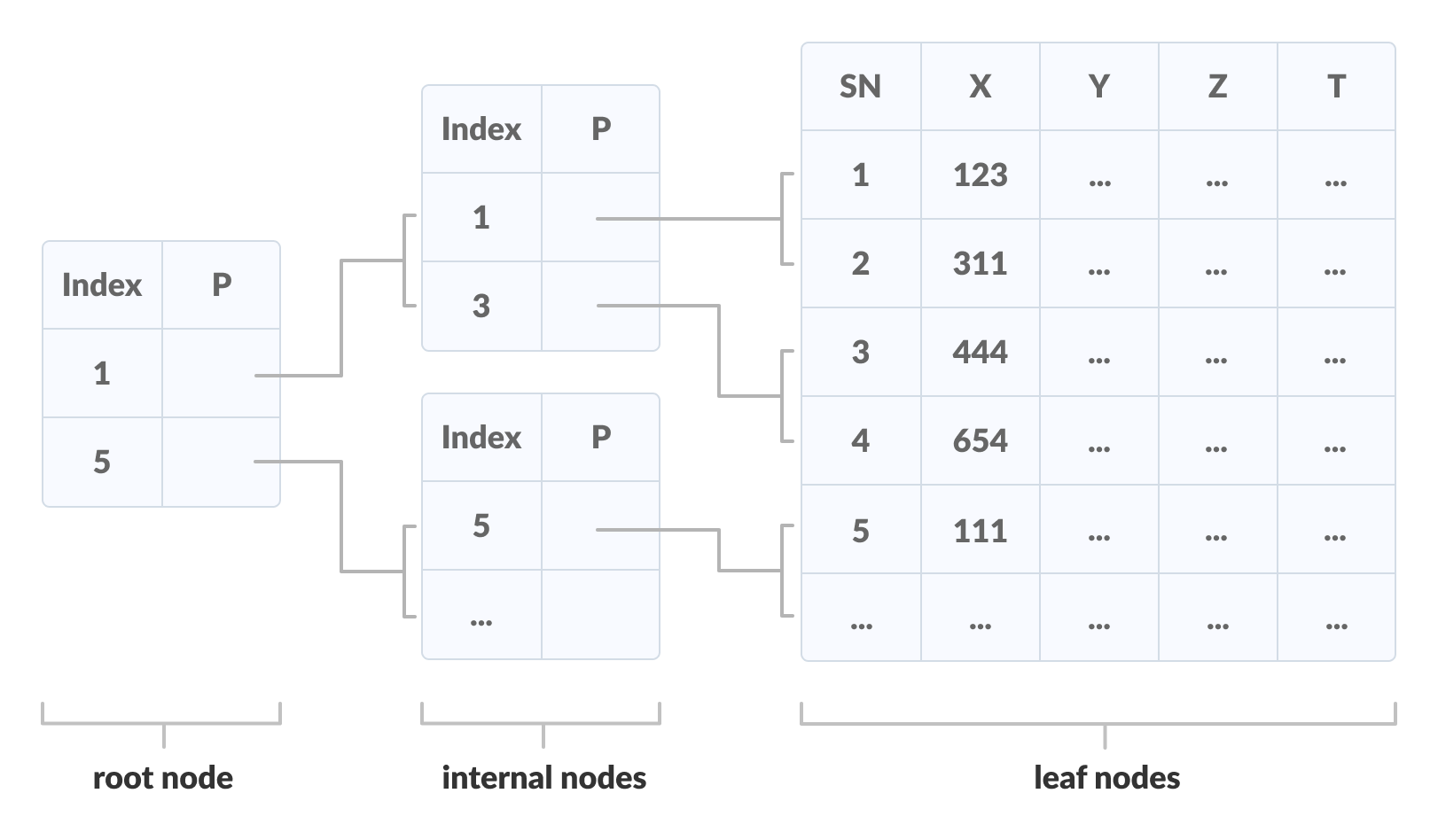使用 B+ 树的多级索引

B+树的性质

  • 所有的叶子都在同一水平线上。
  • 根至少有两个孩子。
  • 除根之外的每个节点最多可以有 m 个子节点和至少 m/2 个子节点。
  • 每个节点最多可以包含 m - 1 个键和至少 ⌈m/2⌉ - 1 个键。

B树和B+树的比较

数据指针仅存在于 B+树的叶节点中，而数据指针可以存在于B树的内部、叶或根节点中。叶子节点在B树上不相互连接，而它们在B+树上相互连接。B+树上的操作比 B树上的操作快。

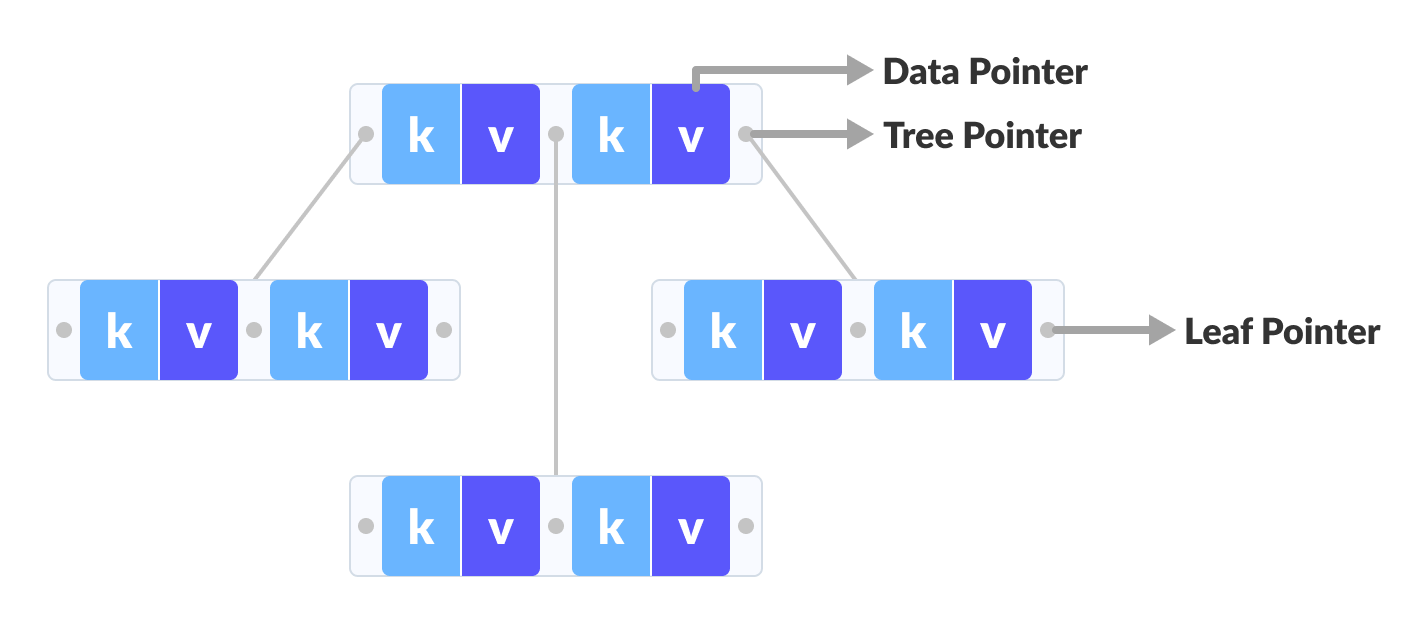B 树 - 图2
B树
B 树 - 图3
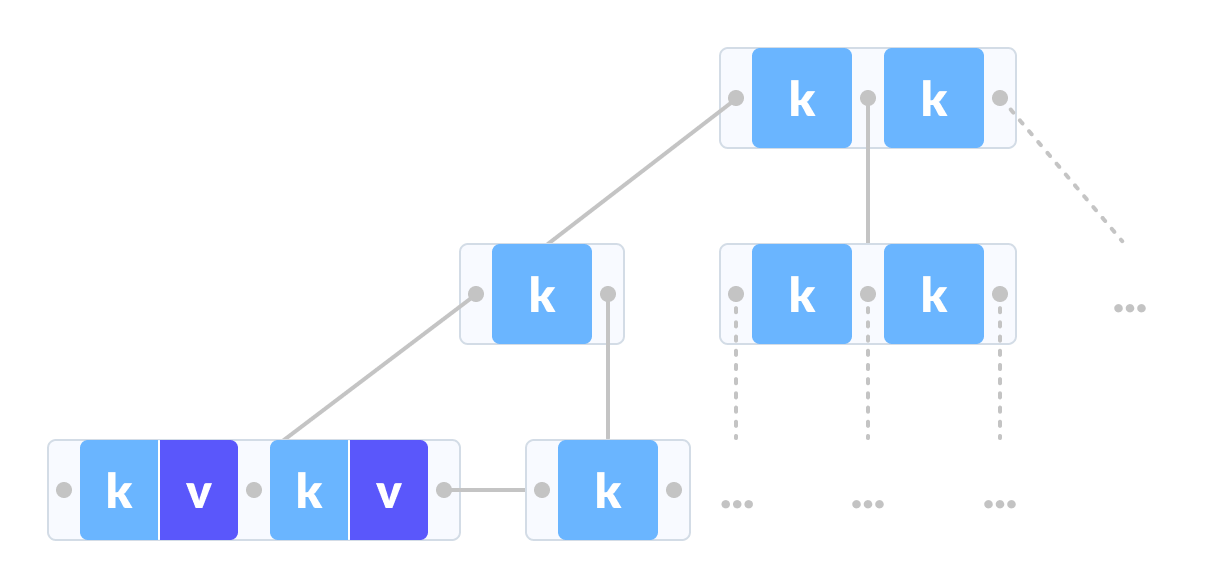B+树

B+树的操作

B+树的搜索

搜索操作

按照以下步骤在B+序树中搜索的数据为k.

  1. 从根节点开始。将 k 与根节点的键进行比较 [k1, k2, k3,……km - 1].
  2. 如果 k < k1，转到根节点的左子节点。
  3. 否则如果 k == k1， 继续和k2比较. 如果k < k2, 则k 介于k1和 k2之间. 所以搜索k2的左子节点.
  4. 如果 k > k2， 继续与 k3, k4,…km -1 重复第 2 步和第 3 步。
  5. 重复以上步骤，直到到达叶子节点。
  6. 如果 k 存在于叶节点中，则返回 true 否则返回 false。

搜索示例

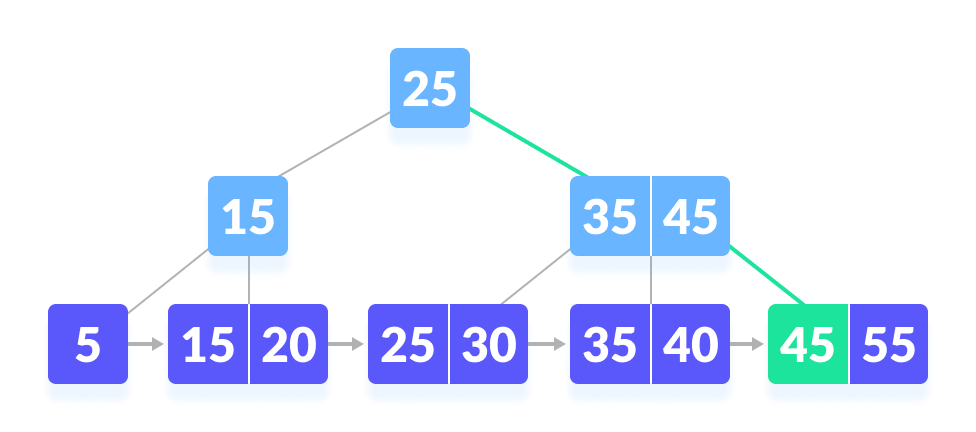
让我们在下面的 B+ 树上搜索 k = 45

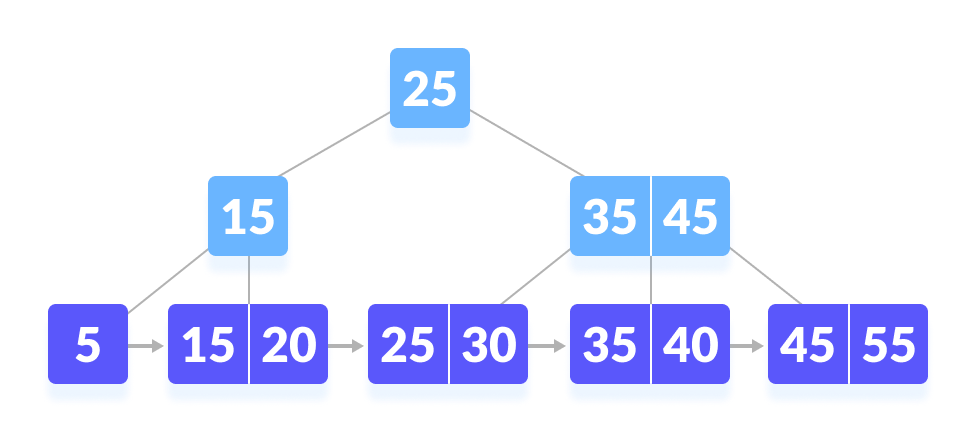B 树 - 图4
B+树
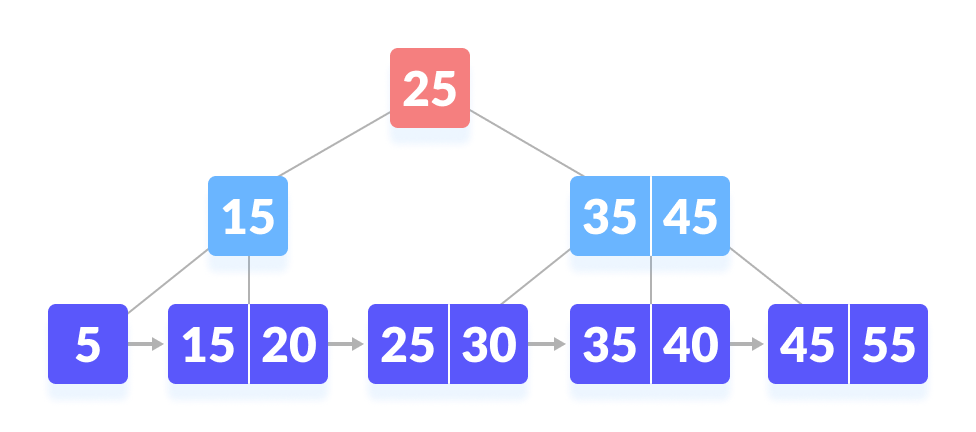
  1. 将 k 与根节点进行比较。 | B 树 - 图5 | | —- | | 在根处找不到 k |
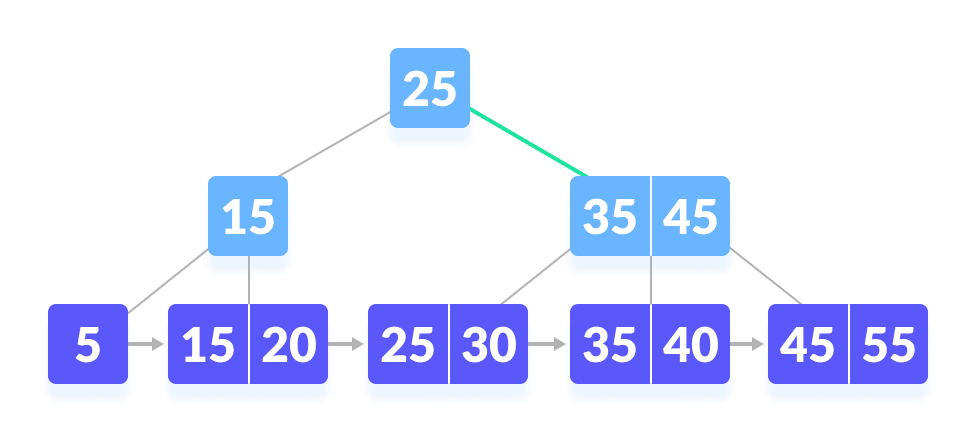
  1. 由于 k > 25，去右孩子。 | B 树 - 图6 | | —- | | 转到根的右侧 |
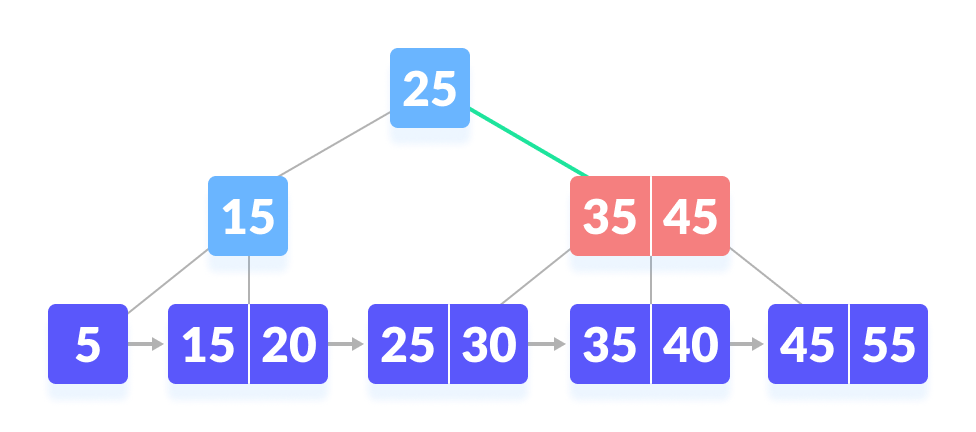
  1. 将 k 与 35 进行比较。由于 k > 30，将 k 与 45 进行比较。 | B 树 - 图7 | | —- | | 没有找到 |
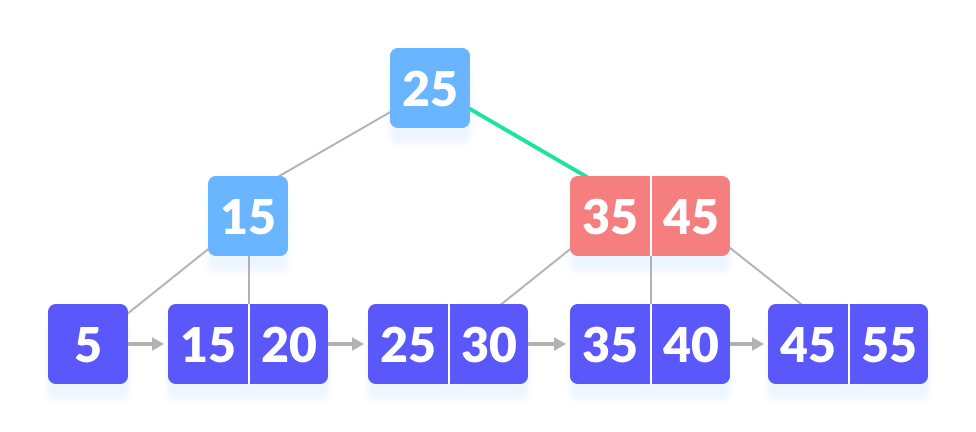
  1. 由于 k ≥ 45，所以继续搜索右孩子。 | B 树 - 图8 | | —- | | 向右走 |
  1. k 被发现。 | B 树 - 图9 | | —- | | 找到 k |

搜索时间复杂度

如果在节点内部实现线性搜索，则总复杂度为 Θ(logt n).
如果使用二分查找，则总复杂度为 Θ(log2t.logt n).

B+树的插入

将元素插入B+ 树包括三个主要事件：搜索适当的叶子、插入元素和平衡/分裂树。

插入约束

插入操作在将元素插入 B+ 树之前，必须牢记这些约束：

  • 根至少有两个孩子。
  • 除根之外的每个节点最多可以有 m 个孩子和至少 m/2 的孩子。
  • 每个节点最多可以包含 m - 1 个键和至少 ⌈m/2⌉ - 1 键。

插入算法

按照以下步骤插入元素。

  1. 由于每个元素都插入到叶节点中，因此请转到相应的叶节点。
  2. 将key插入叶节点。

案例一：叶子节点未满

  1. 如果叶子节点未满，则将key按升序插入叶子节点。

案例二：叶子节点已满

  1. 如果叶子节点已满，则将key按升序插入叶子节点，并按以下方式平衡树。
  2. 在 m/2 位置断开节点。
  3. 将m/2位置的key添加到父节点。
  4. 如果父节点已满，请执行步骤 2 至 3。

插入示例

要插入的元素是 5,15, 25, 35, 45。

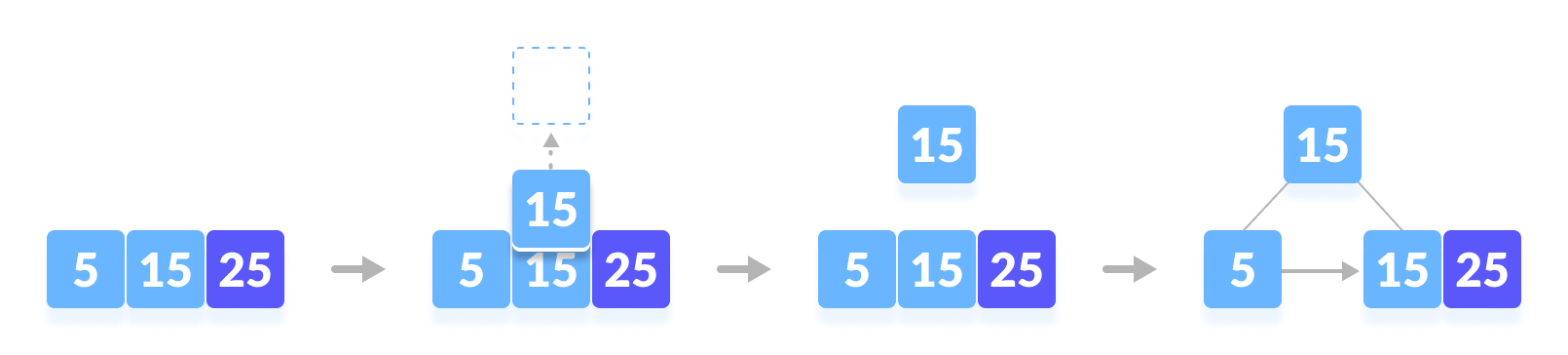
  1. 插入 5 | B 树 - 图10 | | —- | | 插入 5 |

  2. 插入 15 | B 树 - 图11 | | —- | | 插入 15 |

  3. 插入 25。（在 15 位置分裂成2个节点。 将key 15添加到父节点。） | B 树 - 图12 | | —- | | 插入 25 |

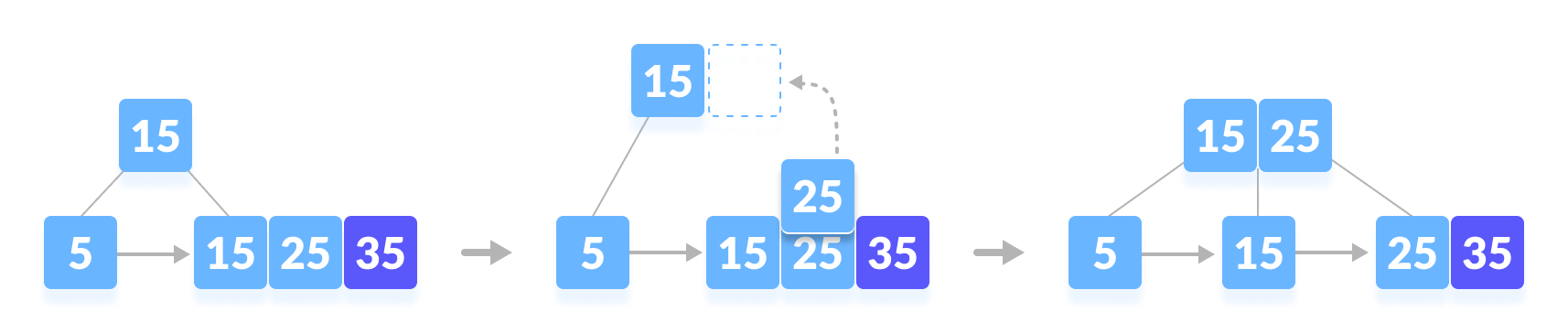
  4. 插入 35（在 25位置分裂成2个节点。 将key 25添加到父节点。） | B 树 - 图13 | | —- | | 插入 35 |

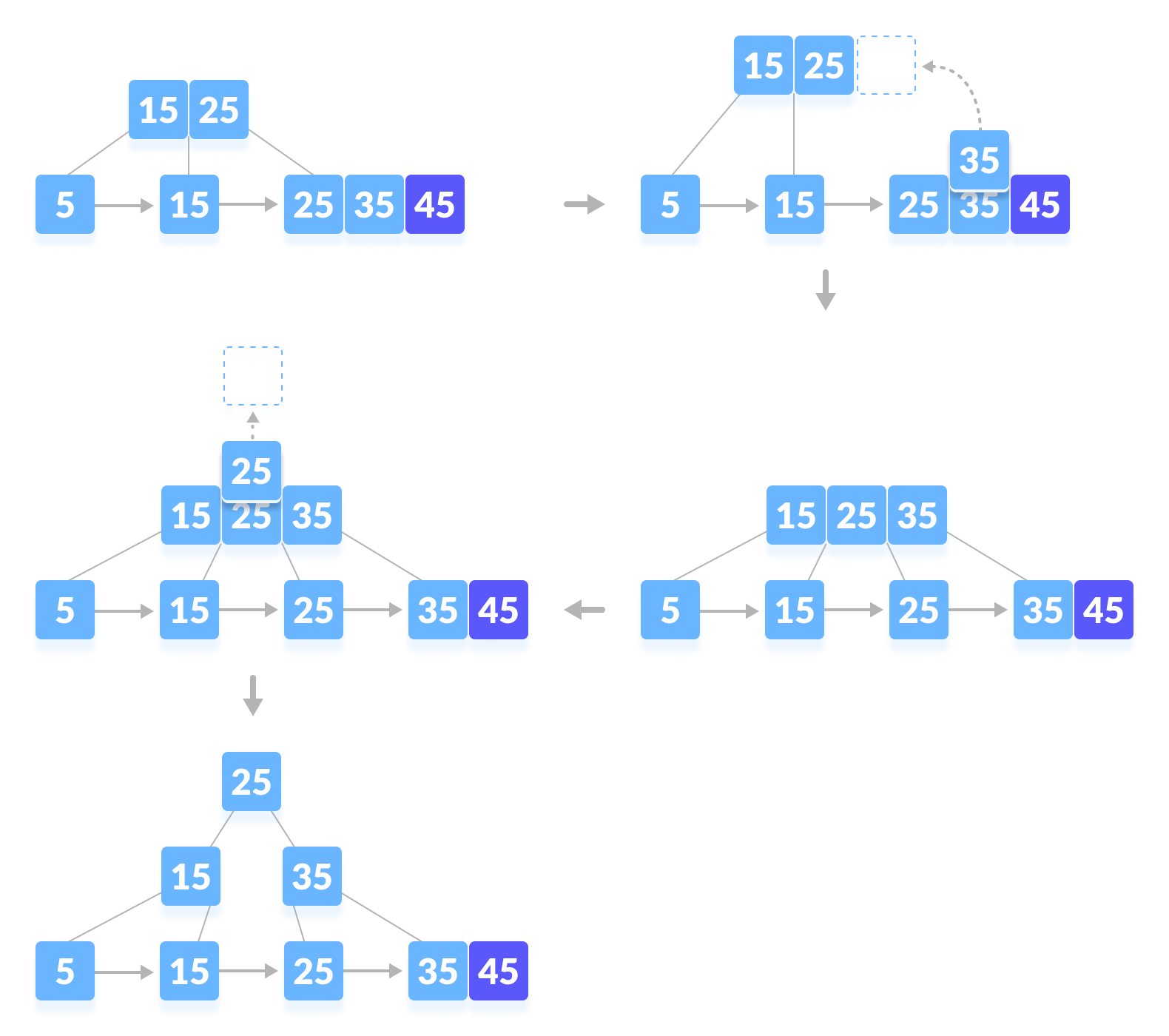
  5. 插入 45 | B 树 - 图14 | | —- | | 插入 45 |

插入复杂度

  • 时间复杂度：Θ(t.logt n)

B+树的删除

删除 B+ 树上的元素包括三个主要事件：搜索要删除的键所在的节点，删除键并在需要时平衡树。下溢是一种情况，当节点中的键数少于它应该保存的最小键数时。

删除约束

在进行以下步骤之前，必须了解有关度数为m（例如m=3）的 B+树的这些事实。

  1. 一个节点最多可以有 m 个子节点。（即 3）
  2. 一个节点最多可以包含 m - 1 个键。（即 2）
  3. 一个节点应该有最少的 ⌈m/2⌉ 个子节点。（即 2）
  4. 一个节点（除了根节点）应该包含最少的⌈m/2⌉ - 1 个键。（即 1）

在删除键时，我们还必须注意内部节点（即索引）中存在的键，因为这些值在 B+ 树中是多余的。搜索要删除的key，然后按照以下步骤操作。

删除算法

案例一：删除的键仅在叶子节点

要删除的键仅存在于叶子节点中，而不存在于索引（或内部节点）中。它有两种情况：

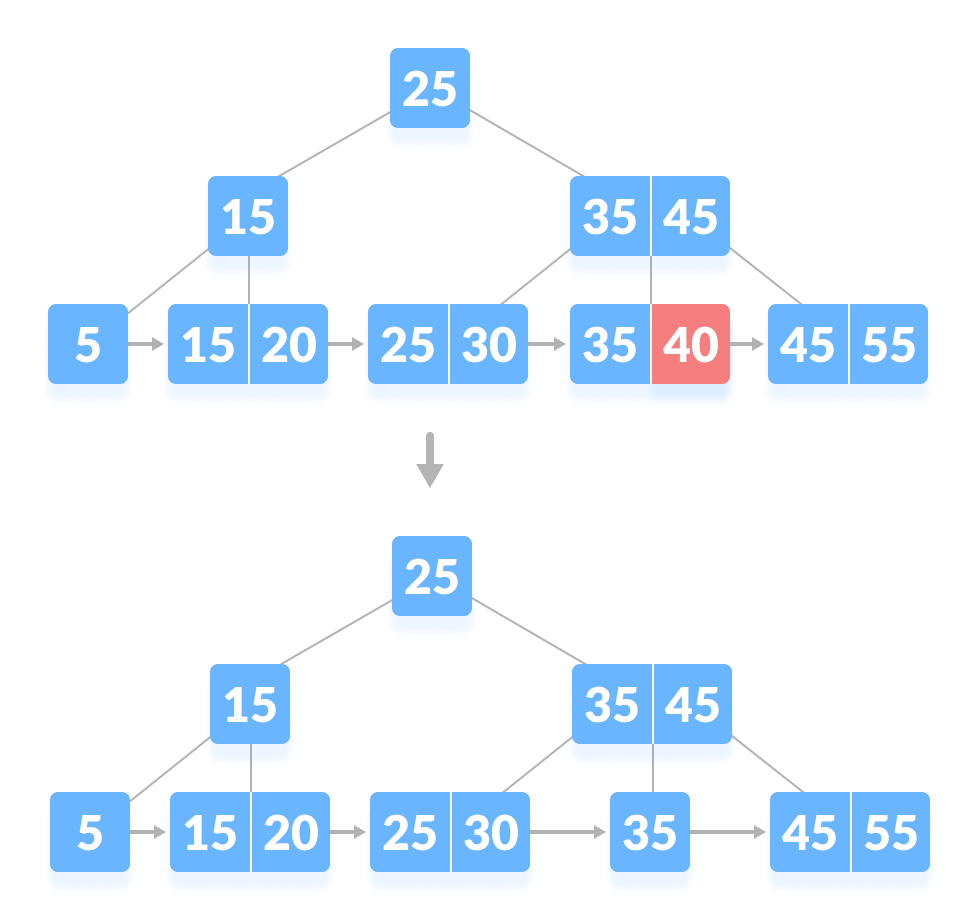  1. 节点中的键数超过最少key数量的约束，只需删除key。 | B 树 - 图15 | | —- | | 从B+树中删除 40 |
  1. 节点中的key数量低于最小约束。删除key并从直接兄弟中借用key。将兄弟节点的中间键添加到父节点。 | 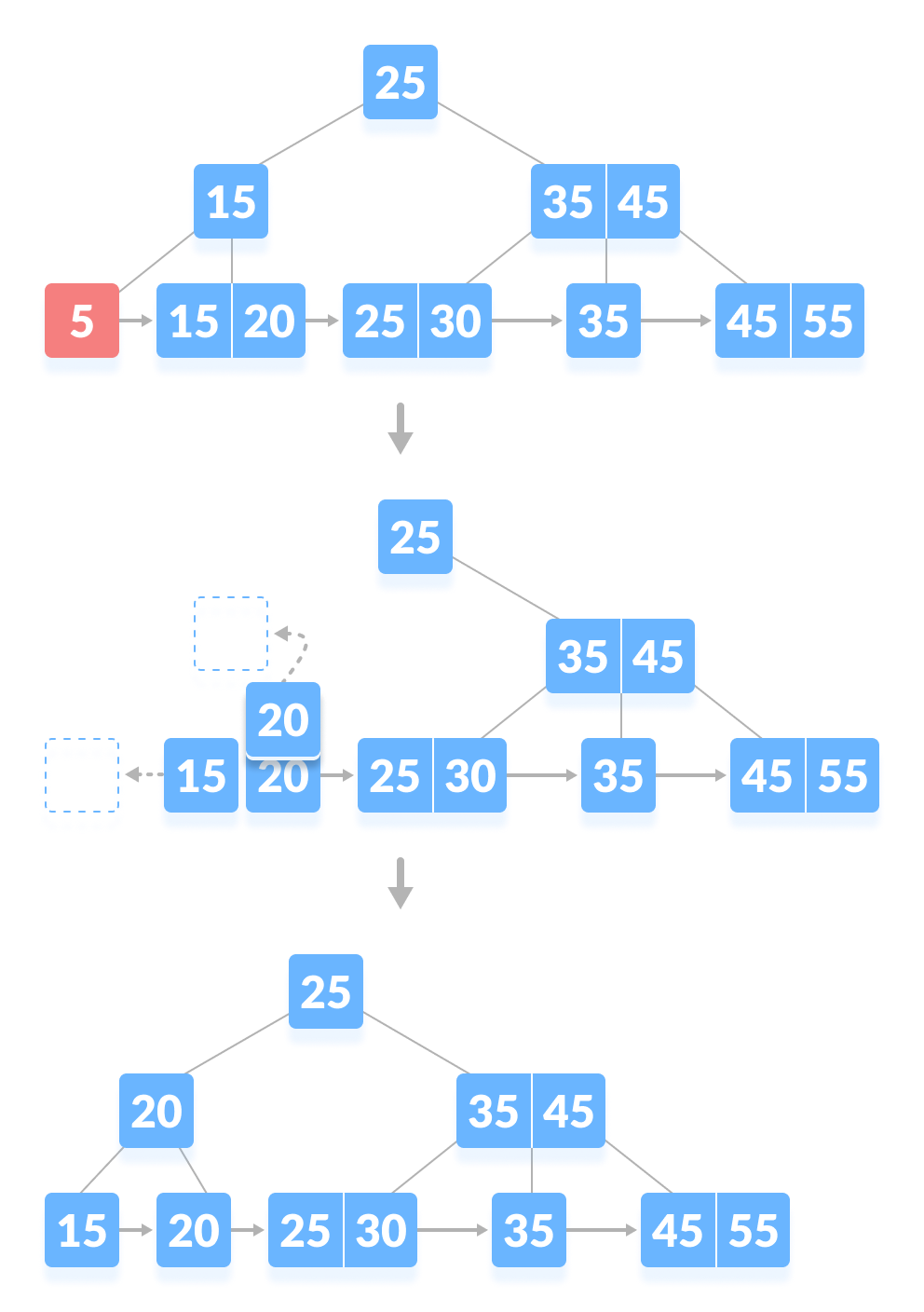B 树 - 图16 | | —- | | 从B+树中删除 5 |

案例二：删除的键也在内部节点

要删除的key即在叶子节点，也存在于内部节点中。然后我们必须从内部节点中删除它们。这种情况有以下几种情况。

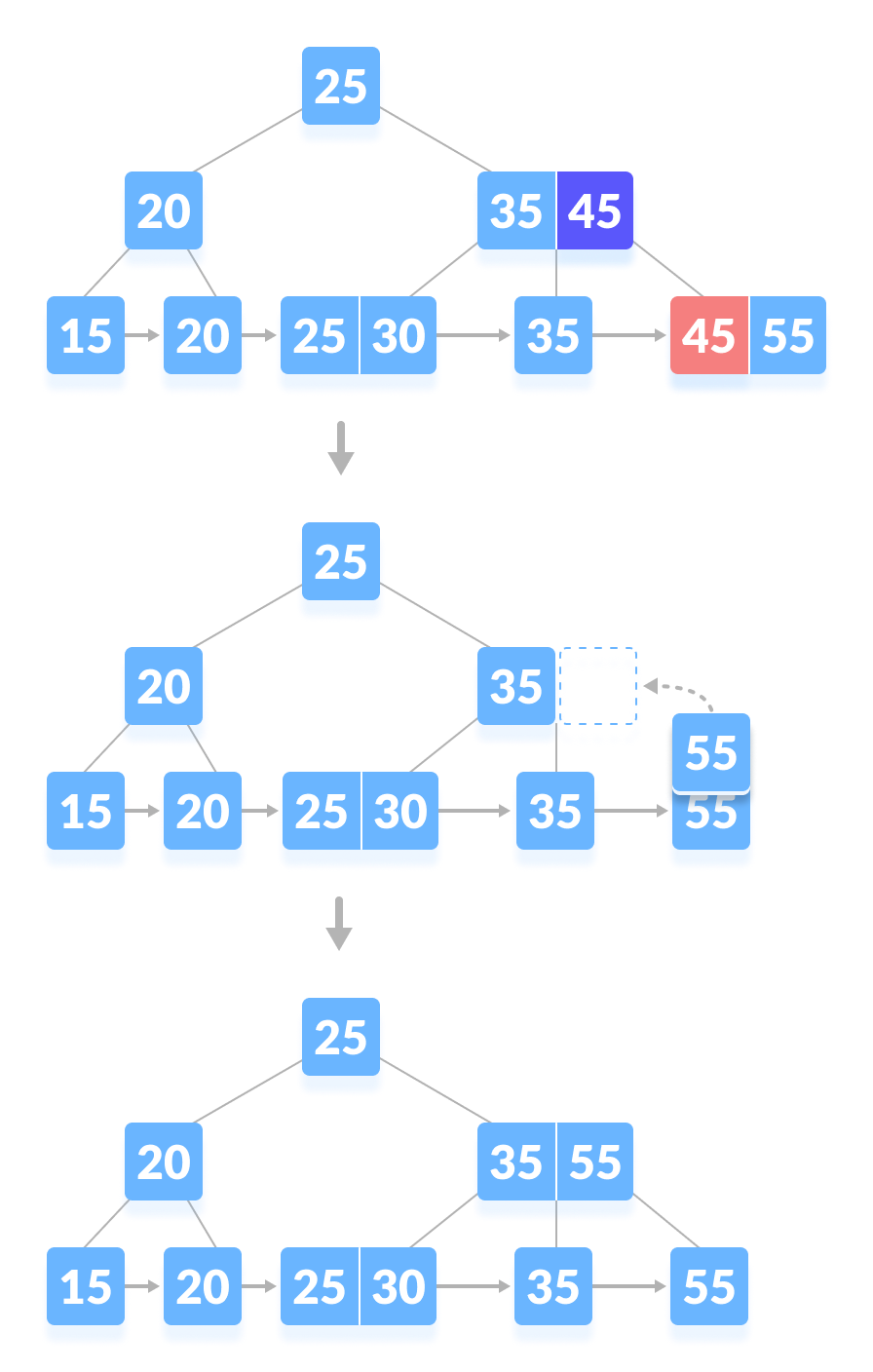  1. 如果节点中的键数量高于最小数量的约束，只需从叶子节点中删除键并从内部节点中删除键即可。用中序后继填充内部节点中的空白空间。 | B 树 - 图17 | | —- | | 从B+树中删除 45 |
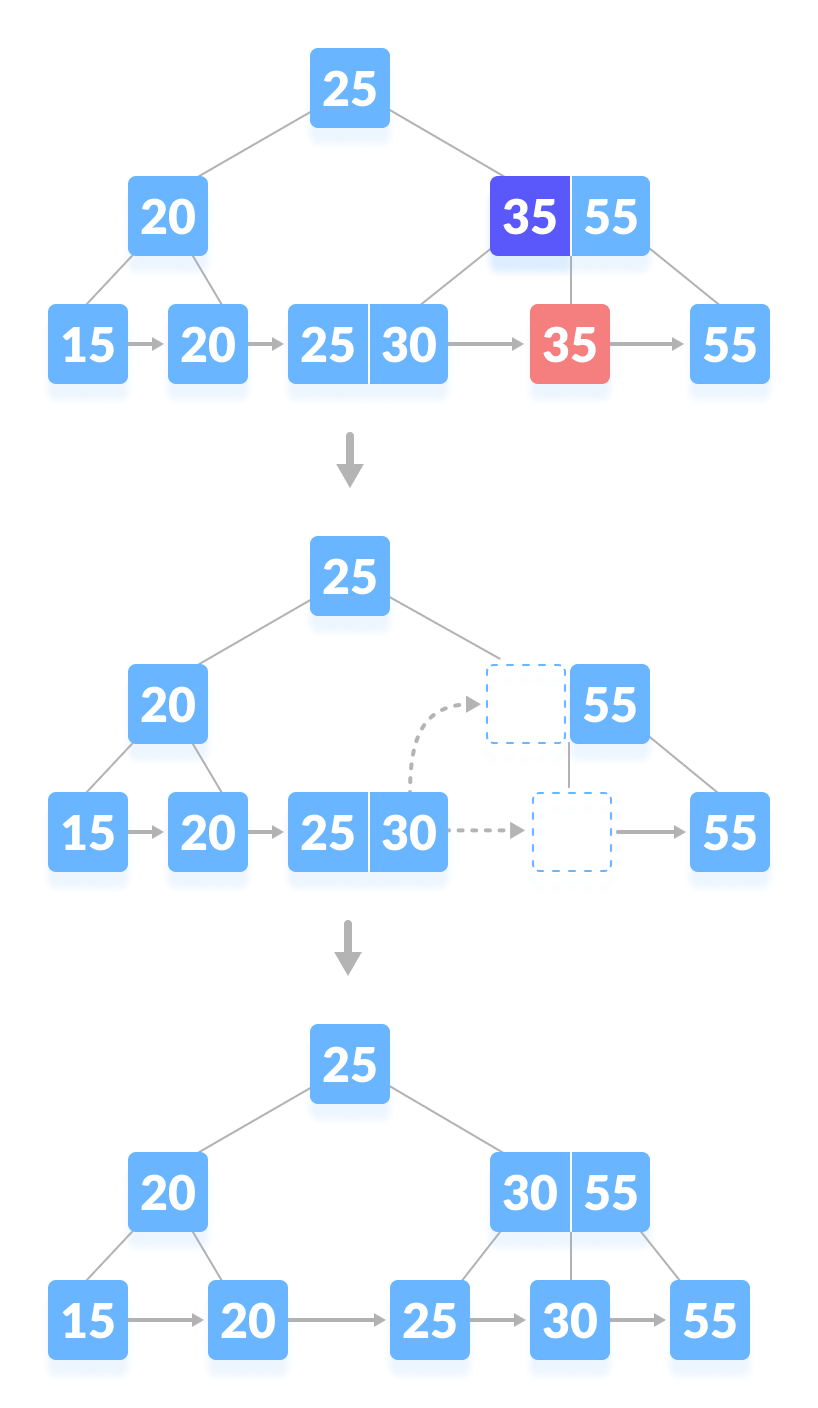  1. 如果节点中的键数低于最小数量的约束，则删除该键并从其直接兄弟（通过父级）借用一个键。用借用的键填充索引（内部节点）中创建的空白空间。 | B 树 - 图18 | | —- | | 从B+树中删除 35 |
  1. 这种情况类似于案例二(1)，但在这里，在直接父节点上方生成空白空间。删除键后，将空白空间（不一定为空）与其兄弟合并。用中序后继节点填充祖父节点中的空白空间。 | 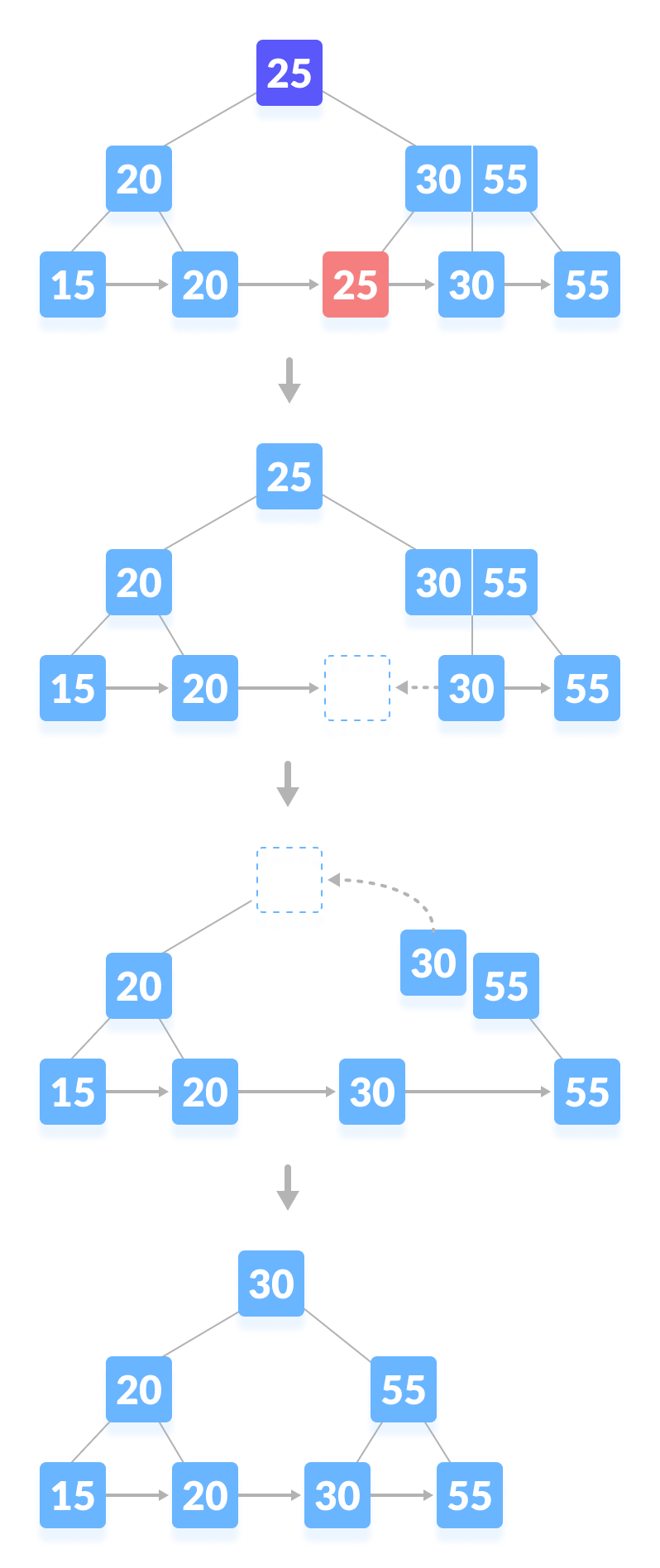B 树 - 图19 | | —- | | 从B+树中删除 25 |

案例三：删除节点导致平衡打破

在这种情况下，树的高度会缩小。有点复杂。从下面的树中删除 55 会导致这种情况。可以在下面的插图中理解。

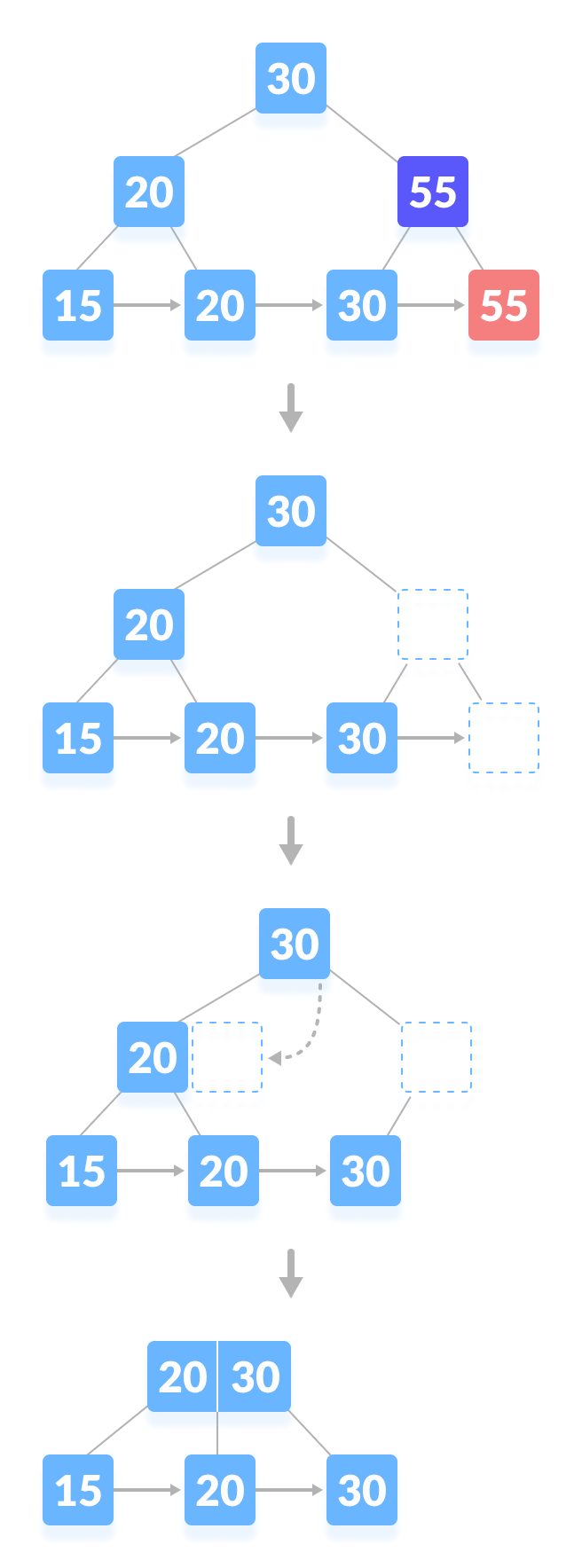B 树 - 图20
从 B 树中删除 55

B+树的应用

  • 多级索引
  • 树上更快的操作（插入、删除、搜索）
  • 数据库索引

B+树的实现

  1. // Searching on a B+ tree in Java
  3. import java.util.*;
  5. public class BPlusTree {
  6.   int m;
  7.   InternalNode root;
  8.   LeafNode firstLeaf;
  10.   // Binary search program
  11.   private int binarySearch(DictionaryPair[] dps, int numPairs, int t) {
  12.     Comparator<DictionaryPair> c = new Comparator<DictionaryPair>() {
  13.       @Override
  14.       public int compare(DictionaryPair o1, DictionaryPair o2) {
  15.         Integer a = Integer.valueOf(o1.key);
  16.         Integer b = Integer.valueOf(o2.key);
  17.         return a.compareTo(b);
  18.       }
  19.     };
  20.     return Arrays.binarySearch(dps, 0, numPairs, new DictionaryPair(t, 0), c);
  21.   }
  23.   // Find the leaf node
  24.   private LeafNode findLeafNode(int key) {
  26.     Integer[] keys = this.root.keys;
  27.     int i;
  29.     for (i = 0; i < this.root.degree - 1; i++) {
  30.       if (key < keys[i]) {
  31.         break;
  32.       }
  33.     }
  35.     Node child = this.root.childPointers[i];
  36.     if (child instanceof LeafNode) {
  37.       return (LeafNode) child;
  38.     } else {
  39.       return findLeafNode((InternalNode) child, key);
  40.     }
  41.   }
  43.   // Find the leaf node
  44.   private LeafNode findLeafNode(InternalNode node, int key) {
  46.     Integer[] keys = node.keys;
  47.     int i;
  49.     for (i = 0; i < node.degree - 1; i++) {
  50.       if (key < keys[i]) {
  51.         break;
  52.       }
  53.     }
  54.     Node childNode = node.childPointers[i];
  55.     if (childNode instanceof LeafNode) {
  56.       return (LeafNode) childNode;
  57.     } else {
  58.       return findLeafNode((InternalNode) node.childPointers[i], key);
  59.     }
  60.   }
  62.   // Finding the index of the pointer
  63.   private int findIndexOfPointer(Node[] pointers, LeafNode node) {
  64.     int i;
  65.     for (i = 0; i < pointers.length; i++) {
  66.       if (pointers[i] == node) {
  67.         break;
  68.       }
  69.     }
  70.     return i;
  71.   }
  73.   // Get the mid point
  74.   private int getMidpoint() {
  75.     return (int) Math.ceil((this.m + 1) / 2.0) - 1;
  76.   }
  78.   // Balance the tree
  79.   private void handleDeficiency(InternalNode in) {
  81.     InternalNode sibling;
  82.     InternalNode parent = in.parent;
  84.     if (this.root == in) {
  85.       for (int i = 0; i < in.childPointers.length; i++) {
  86.         if (in.childPointers[i] != null) {
  87.           if (in.childPointers[i] instanceof InternalNode) {
  88.             this.root = (InternalNode) in.childPointers[i];
  89.             this.root.parent = null;
  90.           } else if (in.childPointers[i] instanceof LeafNode) {
  91.             this.root = null;
  92.           }
  93.         }
  94.       }
  95.     }
  97.     else if (in.leftSibling != null && in.leftSibling.isLendable()) {
  98.       sibling = in.leftSibling;
  99.     } else if (in.rightSibling != null && in.rightSibling.isLendable()) {
  100.       sibling = in.rightSibling;
  102.       int borrowedKey = sibling.keys[0];
  103.       Node pointer = sibling.childPointers[0];
  105.       in.keys[in.degree - 1] = parent.keys[0];
  106.       in.childPointers[in.degree] = pointer;
  108.       parent.keys[0] = borrowedKey;
  110.       sibling.removePointer(0);
  111.       Arrays.sort(sibling.keys);
  112.       sibling.removePointer(0);
  113.       shiftDown(in.childPointers, 1);
  114.     } else if (in.leftSibling != null && in.leftSibling.isMergeable()) {
  116.     } else if (in.rightSibling != null && in.rightSibling.isMergeable()) {
  117.       sibling = in.rightSibling;
  118.       sibling.keys[sibling.degree - 1] = parent.keys[parent.degree - 2];
  119.       Arrays.sort(sibling.keys, 0, sibling.degree);
  120.       parent.keys[parent.degree - 2] = null;
  122.       for (int i = 0; i < in.childPointers.length; i++) {
  123.         if (in.childPointers[i] != null) {
  124.           sibling.prependChildPointer(in.childPointers[i]);
  125.           in.childPointers[i].parent = sibling;
  126.           in.removePointer(i);
  127.         }
  128.       }
  130.       parent.removePointer(in);
  132.       sibling.leftSibling = in.leftSibling;
  133.     }
  135.     if (parent != null && parent.isDeficient()) {
  136.       handleDeficiency(parent);
  137.     }
  138.   }
  140.   private boolean isEmpty() {
  141.     return firstLeaf == null;
  142.   }
  144.   private int linearNullSearch(DictionaryPair[] dps) {
  145.     for (int i = 0; i < dps.length; i++) {
  146.       if (dps[i] == null) {
  147.         return i;
  148.       }
  149.     }
  150.     return -1;
  151.   }
  153.   private int linearNullSearch(Node[] pointers) {
  154.     for (int i = 0; i < pointers.length; i++) {
  155.       if (pointers[i] == null) {
  156.         return i;
  157.       }
  158.     }
  159.     return -1;
  160.   }
  162.   private void shiftDown(Node[] pointers, int amount) {
  163.     Node[] newPointers = new Node[this.m + 1];
  164.     for (int i = amount; i < pointers.length; i++) {
  165.       newPointers[i - amount] = pointers[i];
  166.     }
  167.     pointers = newPointers;
  168.   }
  170.   private void sortDictionary(DictionaryPair[] dictionary) {
  171.     Arrays.sort(dictionary, new Comparator<DictionaryPair>() {
  172.       @Override
  173.       public int compare(DictionaryPair o1, DictionaryPair o2) {
  174.         if (o1 == null && o2 == null) {
  175.           return 0;
  176.         }
  177.         if (o1 == null) {
  178.           return 1;
  179.         }
  180.         if (o2 == null) {
  181.           return -1;
  182.         }
  183.         return o1.compareTo(o2);
  184.       }
  185.     });
  186.   }
  188.   private Node[] splitChildPointers(InternalNode in, int split) {
  190.     Node[] pointers = in.childPointers;
  191.     Node[] halfPointers = new Node[this.m + 1];
  193.     for (int i = split + 1; i < pointers.length; i++) {
  194.       halfPointers[i - split - 1] = pointers[i];
  195.       in.removePointer(i);
  196.     }
  198.     return halfPointers;
  199.   }
  201.   private DictionaryPair[] splitDictionary(LeafNode ln, int split) {
  203.     DictionaryPair[] dictionary = ln.dictionary;
  205.     DictionaryPair[] halfDict = new DictionaryPair[this.m];
  207.     for (int i = split; i < dictionary.length; i++) {
  208.       halfDict[i - split] = dictionary[i];
  209.       ln.delete(i);
  210.     }
  212.     return halfDict;
  213.   }
  215.   private void splitInternalNode(InternalNode in) {
  217.     InternalNode parent = in.parent;
  219.     int midpoint = getMidpoint();
  220.     int newParentKey = in.keys[midpoint];
  221.     Integer[] halfKeys = splitKeys(in.keys, midpoint);
  222.     Node[] halfPointers = splitChildPointers(in, midpoint);
  224.     in.degree = linearNullSearch(in.childPointers);
  226.     InternalNode sibling = new InternalNode(this.m, halfKeys, halfPointers);
  227.     for (Node pointer : halfPointers) {
  228.       if (pointer != null) {
  229.         pointer.parent = sibling;
  230.       }
  231.     }
  233.     sibling.rightSibling = in.rightSibling;
  234.     if (sibling.rightSibling != null) {
  235.       sibling.rightSibling.leftSibling = sibling;
  236.     }
  237.     in.rightSibling = sibling;
  238.     sibling.leftSibling = in;
  240.     if (parent == null) {
  242.       Integer[] keys = new Integer[this.m];
  243.       keys[0] = newParentKey;
  244.       InternalNode newRoot = new InternalNode(this.m, keys);
  245.       newRoot.appendChildPointer(in);
  246.       newRoot.appendChildPointer(sibling);
  247.       this.root = newRoot;
  249.       in.parent = newRoot;
  250.       sibling.parent = newRoot;
  252.     } else {
  254.       parent.keys[parent.degree - 1] = newParentKey;
  255.       Arrays.sort(parent.keys, 0, parent.degree);
  257.       int pointerIndex = parent.findIndexOfPointer(in) + 1;
  258.       parent.insertChildPointer(sibling, pointerIndex);
  259.       sibling.parent = parent;
  260.     }
  261.   }
  263.   private Integer[] splitKeys(Integer[] keys, int split) {
  265.     Integer[] halfKeys = new Integer[this.m];
  267.     keys[split] = null;
  269.     for (int i = split + 1; i < keys.length; i++) {
  270.       halfKeys[i - split - 1] = keys[i];
  271.       keys[i] = null;
  272.     }
  274.     return halfKeys;
  275.   }
  277.   public void insert(int key, double value) {
  278.     if (isEmpty()) {
  280.       LeafNode ln = new LeafNode(this.m, new DictionaryPair(key, value));
  282.       this.firstLeaf = ln;
  284.     } else {
  285.       LeafNode ln = (this.root == null) ? this.firstLeaf : findLeafNode(key);
  287.       if (!ln.insert(new DictionaryPair(key, value))) {
  289.         ln.dictionary[ln.numPairs] = new DictionaryPair(key, value);
  290.         ln.numPairs++;
  291.         sortDictionary(ln.dictionary);
  293.         int midpoint = getMidpoint();
  294.         DictionaryPair[] halfDict = splitDictionary(ln, midpoint);
  296.         if (ln.parent == null) {
  298.           Integer[] parent_keys = new Integer[this.m];
  299.           parent_keys[0] = halfDict[0].key;
  300.           InternalNode parent = new InternalNode(this.m, parent_keys);
  301.           ln.parent = parent;
  302.           parent.appendChildPointer(ln);
  304.         } else {
  305.           int newParentKey = halfDict[0].key;
  306.           ln.parent.keys[ln.parent.degree - 1] = newParentKey;
  307.           Arrays.sort(ln.parent.keys, 0, ln.parent.degree);
  308.         }
  310.         LeafNode newLeafNode = new LeafNode(this.m, halfDict, ln.parent);
  312.         int pointerIndex = ln.parent.findIndexOfPointer(ln) + 1;
  313.         ln.parent.insertChildPointer(newLeafNode, pointerIndex);
  315.         newLeafNode.rightSibling = ln.rightSibling;
  316.         if (newLeafNode.rightSibling != null) {
  317.           newLeafNode.rightSibling.leftSibling = newLeafNode;
  318.         }
  319.         ln.rightSibling = newLeafNode;
  320.         newLeafNode.leftSibling = ln;
  322.         if (this.root == null) {
  324.           this.root = ln.parent;
  326.         } else {
  327.           InternalNode in = ln.parent;
  328.           while (in != null) {
  329.             if (in.isOverfull()) {
  330.               splitInternalNode(in);
  331.             } else {
  332.               break;
  333.             }
  334.             in = in.parent;
  335.           }
  336.         }
  337.       }
  338.     }
  339.   }
  341.   public Double search(int key) {
  343.     if (isEmpty()) {
  344.       return null;
  345.     }
  347.     LeafNode ln = (this.root == null) ? this.firstLeaf : findLeafNode(key);
  349.     DictionaryPair[] dps = ln.dictionary;
  350.     int index = binarySearch(dps, ln.numPairs, key);
  352.     if (index < 0) {
  353.       return null;
  354.     } else {
  355.       return dps[index].value;
  356.     }
  357.   }
  359.   public ArrayList<Double> search(int lowerBound, int upperBound) {
  361.     ArrayList<Double> values = new ArrayList<Double>();
  363.     LeafNode currNode = this.firstLeaf;
  364.     while (currNode != null) {
  366.       DictionaryPair dps[] = currNode.dictionary;
  367.       for (DictionaryPair dp : dps) {
  369.         if (dp == null) {
  370.           break;
  371.         }
  373.         if (lowerBound <= dp.key && dp.key <= upperBound) {
  374.           values.add(dp.value);
  375.         }
  376.       }
  377.       currNode = currNode.rightSibling;
  379.     }
  381.     return values;
  382.   }
  384.   public BPlusTree(int m) {
  385.     this.m = m;
  386.     this.root = null;
  387.   }
  389.   public class Node {
  390.     InternalNode parent;
  391.   }
  393.   private class InternalNode extends Node {
  394.     int maxDegree;
  395.     int minDegree;
  396.     int degree;
  397.     InternalNode leftSibling;
  398.     InternalNode rightSibling;
  399.     Integer[] keys;
  400.     Node[] childPointers;
  402.     private void appendChildPointer(Node pointer) {
  403.       this.childPointers[degree] = pointer;
  404.       this.degree++;
  405.     }
  407.     private int findIndexOfPointer(Node pointer) {
  408.       for (int i = 0; i < childPointers.length; i++) {
  409.         if (childPointers[i] == pointer) {
  410.           return i;
  411.         }
  412.       }
  413.       return -1;
  414.     }
  416.     private void insertChildPointer(Node pointer, int index) {
  417.       for (int i = degree - 1; i >= index; i--) {
  418.         childPointers[i + 1] = childPointers[i];
  419.       }
  420.       this.childPointers[index] = pointer;
  421.       this.degree++;
  422.     }
  424.     private boolean isDeficient() {
  425.       return this.degree < this.minDegree;
  426.     }
  428.     private boolean isLendable() {
  429.       return this.degree > this.minDegree;
  430.     }
  432.     private boolean isMergeable() {
  433.       return this.degree == this.minDegree;
  434.     }
  436.     private boolean isOverfull() {
  437.       return this.degree == maxDegree + 1;
  438.     }
  440.     private void prependChildPointer(Node pointer) {
  441.       for (int i = degree - 1; i >= 0; i--) {
  442.         childPointers[i + 1] = childPointers[i];
  443.       }
  444.       this.childPointers[0] = pointer;
  445.       this.degree++;
  446.     }
  448.     private void removeKey(int index) {
  449.       this.keys[index] = null;
  450.     }
  452.     private void removePointer(int index) {
  453.       this.childPointers[index] = null;
  454.       this.degree--;
  455.     }
  457.     private void removePointer(Node pointer) {
  458.       for (int i = 0; i < childPointers.length; i++) {
  459.         if (childPointers[i] == pointer) {
  460.           this.childPointers[i] = null;
  461.         }
  462.       }
  463.       this.degree--;
  464.     }
  466.     private InternalNode(int m, Integer[] keys) {
  467.       this.maxDegree = m;
  468.       this.minDegree = (int) Math.ceil(m / 2.0);
  469.       this.degree = 0;
  470.       this.keys = keys;
  471.       this.childPointers = new Node[this.maxDegree + 1];
  472.     }
  474.     private InternalNode(int m, Integer[] keys, Node[] pointers) {
  475.       this.maxDegree = m;
  476.       this.minDegree = (int) Math.ceil(m / 2.0);
  477.       this.degree = linearNullSearch(pointers);
  478.       this.keys = keys;
  479.       this.childPointers = pointers;
  480.     }
  481.   }
  483.   public class LeafNode extends Node {
  484.     int maxNumPairs;
  485.     int minNumPairs;
  486.     int numPairs;
  487.     LeafNode leftSibling;
  488.     LeafNode rightSibling;
  489.     DictionaryPair[] dictionary;
  491.     public void delete(int index) {
  492.       this.dictionary[index] = null;
  493.       numPairs--;
  494.     }
  496.     public boolean insert(DictionaryPair dp) {
  497.       if (this.isFull()) {
  498.         return false;
  499.       } else {
  500.         this.dictionary[numPairs] = dp;
  501.         numPairs++;
  502.         Arrays.sort(this.dictionary, 0, numPairs);
  504.         return true;
  505.       }
  506.     }
  508.     public boolean isDeficient() {
  509.       return numPairs < minNumPairs;
  510.     }
  512.     public boolean isFull() {
  513.       return numPairs == maxNumPairs;
  514.     }
  516.     public boolean isLendable() {
  517.       return numPairs > minNumPairs;
  518.     }
  520.     public boolean isMergeable() {
  521.       return numPairs == minNumPairs;
  522.     }
  524.     public LeafNode(int m, DictionaryPair dp) {
  525.       this.maxNumPairs = m - 1;
  526.       this.minNumPairs = (int) (Math.ceil(m / 2) - 1);
  527.       this.dictionary = new DictionaryPair[m];
  528.       this.numPairs = 0;
  529.       this.insert(dp);
  530.     }
  532.     public LeafNode(int m, DictionaryPair[] dps, InternalNode parent) {
  533.       this.maxNumPairs = m - 1;
  534.       this.minNumPairs = (int) (Math.ceil(m / 2) - 1);
  535.       this.dictionary = dps;
  536.       this.numPairs = linearNullSearch(dps);
  537.       this.parent = parent;
  538.     }
  539.   }
  541.   public class DictionaryPair implements Comparable<DictionaryPair> {
  542.     int key;
  543.     double value;
  545.     public DictionaryPair(int key, double value) {
  546.       this.key = key;
  547.       this.value = value;
  548.     }
  550.     public int compareTo(DictionaryPair o) {
  551.       if (key == o.key) {
  552.         return 0;
  553.       } else if (key > o.key) {
  554.         return 1;
  555.       } else {
  556.         return -1;
  557.       }
  558.     }
  559.   }
  561.   public static void main(String[] args) {
  562.     BPlusTree bpt = null;
  563.     bpt = new BPlusTree(3);
  564.     bpt.insert(5, 33);
  565.     bpt.insert(15, 21);
  566.     bpt.insert(25, 31);
  567.     bpt.insert(35, 41);
  568.     bpt.insert(45, 10);
  570.     if (bpt.search(15) != null) {
  571.       System.out.println("Found");
  572.     } else {
  573.       System.out.println("Not Found");
  574.     }
  575.     ;
  576.   }
  577. }