遍历

先序遍历

  1. //递归
  2. void PreOrder(BiTree T){
  3.     if(T!=NULL){
  4.         visit(T);
  5.         PreOrder(T->lchild);
  6.         PreOrder(T->rchild);
  7.     }
  8. }
  9. //非递归,用栈
  10. void PreOrder(BiTNode *bt){
  11.     if(bt!=NULL){
  12.         BiTNode *Stack[maxsize];//手动模拟栈
  13.         int top=-1;
  14.         BiTNode *p;
  15.         Stack[++top]=bt;//根结点入栈
  16.         while(top!=-1){
  17.             p=Stack[top--];
  18.             visit(p);
  19.             if(p->rchild!=NULL)//应该让右孩子先入栈
  20.                 Stack[++top]=p->rchild;
  21.             if(p->lchild!=NULL)
  22.                 Stack[++top]=p->lchild;
  23.         }//while
  24.     }
  25. }

中序遍历

  1. //递归
  2. void InOrder(BiTree T){
  3.     if(T!=NULL){
  4.         InOrder(T->lchild);
  5.         visit(T);
  6.         InOrder(T->rchild);
  7.     }
  8. }
  10. //非递归
  11. void InOrder(BiTNode *bt){
  12.     if(bt!=NULL){
  13.         BiTNode *Stack[maxsize];
  14.         int top=-1;
  15.         BiTNode *p=bt;
  16.         while(top!=-1||p!=NULL){
  17.             if(p){
  18.                 Stack[++top]=p;
  19.                 p=p->lchild;
  20.             }
  21.             else{
  22.                 p=Stack[top--];
  23.                 visit(p);
  24.                 p=p->rchild;
  25.             }
  26.         }
  27.     }

后序遍历

  1. //递归
  2. void PostOrder(BiTree T){
  3.     if(T!=NULL){
  4.         PostOrder(T->lchild);
  5.         PostOrder(T->rchild);
  6.         visit(T);
  7.     }
  8. }
  10. typedef struct BiTNode{
  11.     ElemType data;
  12.     struct BiTNode *lchild,*rchild;
  13.     int tag;//访问位，0表示未访问，1表示已访问
  14. }BiTNode,*BiTree;
  15. //非递归
  16. void PostOrder(BiTNode *bt){
  17.     if(T!=NULL){
  18.         BiTNode *Stack[maxsize];
  19.         int top=-1;
  20.         BiTNode *p=T;
  21.         while(top!=-1||p!=NULL){
  22.             if(p){
  23.                 Stack[++top]=p;
  24.                 p=p->lchild;
  25.             }
  26.             else{
  27.                 p=Stack[top--];
  28.                 if(p->lchild&&(p->lchild->tag==0)){
  29.                     Stack[++top]=p;
  30.                     p=p->rchild;
  31.                 }
  32.                 else{
  33.                     visit(p);
  34.                     p->tag=1;
  35.                     p=NULL;
  36.                 }
  37.             }
  38.         }
  39.     }

层序遍历

  1. typedef struct Queue{
  2.     BiTNode *data[maxsize];
  3.     int front,rear;
  4. }Queue;
  5. //借助队列
  6. void LevelOrder(BiTNode *bt){
  7.     Queue Q;
  8.     InitStack(Q);
  9.     EnQueue(Q,bt);
  10.     BiTNode *P;
  11.     while(isEmpty(Q)){
  12.         DeQueue(Q,p);
  13.         visit(p);
  14.         if(p->lchild!=NULL)
  15.             EnQueue(Q,p->lchild);
  16.         if(p->rchild!=NULL)
  17.             EnQueue(Q,p->rchild);
  18.     }
  19. }
  20. //手动模拟队列
  21. void LevelOrder(BiTNode *bt){
  22.     BiTNode *Q[maxsize];
  23.     int front=rear=0;
  24.     BiTNode *p;
  25.     if(bt!=NULL){
  26.         rear=(rear+1)%maxsize;
  27.         Q[rear]=bt;
  28.         while(front!=rear){
  29.             front=(front+1)%maxsize;
  30.             p=Q[front];
  31.             visit(p);
  32.             if(p->lchild!=NULL){
  33.                 rear=(rear+1)%maxsize;
  34.                 Q[rear]=p->lchild;
  35.             }
  36.             if(p->rchild!=NULL){
  37.                 rear=(rear+1)%maxsize;
  38.                 Q[rear]p->rchild;
  39.             }
  40.         }//while
  41.     }
  42. }

1. 试编写二叉树的自下而上、从右到左的层次遍历算法。
【算法思想】
一般的二叉树层次遍历是自上而下，自左到右。在这里刚好相反。我们利用原有的层次遍历算法，各结点出队的同时将各结点指针入栈，在所有结点入栈后再从 栈顶开始依次访问。

  1. void InvertLevelOrder(BiTree bt){
  2.     Stack S;
  3.     Queue Q;
  4.     if(bt!=NULL){
  5.         InitStack(S);
  6.         InitQueue(Q);
  7.         EnQueue(Q,bt);
  8.         BiTNode *P;
  9.         while(!IsEmpty(Q)){
  10.             DeQueue(Q,p);
  11.             Push(S,p);
  12.             if(p->lchild)
  13.                 EnQueue(Q,P->lchild);
  14.             if(p->rchild)
  15.                 EnQueue(Q,p->rchild);
  16.         }
  17.         while(!IsEmpty(S)){
  18.             Pop(S,p);
  19.             visit(p);//自下而上，从右到左的遍历
  20.         }
  21.     }//if
  22. }

2.设二叉树采用二叉链表的存储结构，试着编写非递归算法二叉树的高度。
【算法思想】
采用层次遍历的算法，设置变量 level 记录当前结点所在的层次，设置变量 last指向当前层的最右结点。每层次遍历出队时与 last 指针比较，若两者相等，则层数+1，并且计算下一层的最右结点，直到遍历完成。level 的值即为二叉树的高度

  1. int BtDepth(BiTree T){
  2.     if(T==NULL)
  3.         return 0;
  4.     else{
  5.         //采用手动模拟队列方式
  6.         int front=rear=-1;
  7.         int last=level=0;
  8.         BiTree *Q[maxsize];
  9.         Q[++rear]=T;
  10.         BiTree p;
  11.         while(front<rear){
  12.             p=Q[++front];
  13.             if(p->lchild)
  14.                 Q[++rear]=p->lchild;
  15.             if(p->rchild)
  16.                 Q[++rear]=p->rchild;
  17.             if(front==last){
  18.                 level++;
  19.                 last=rear;
  20.             }
  21.         }//while
  22.         return level;
  23.     }
  24. }
  25. //递归实现
  26. int BtDepth(BiTree T){
  27.     if(T==NULL)
  28.         return 0;
  29.     ldep=BtDepth(T->lchild);
  30.     rdep=BtDepth(T->rchild);
  31.     if(ldep>rdep)
  32.         return ldep+1;
  33.     else
  34.         return rdep+1;
  35. }

3.计算二叉树的最大宽度（二叉树的最大宽度是指二叉树所有层中结点个数的最大值） 

  1. //采用level数组记录每个结点所在层次
  2. int BtWidth(BiTree T){
  3.     if(T==NULL)
  4.         return 0;
  5.     BiTree p;
  6.     int k;//记录结点所在层次
  7.     BiTree *Q[maxsize];
  8.     int front=rear=-1;
  9.     int level[maxsize];
  10.     Q[++rear]=T;
  11.     level[rear]=1;//根结点层次为1
  12.     while(front<rear){
  13.         p=Q[++front];//出队结点
  14.         k=level[front];//出队结点的层次
  15.         if(p->lchild){
  16.             Q[++rear]=p->lchild;
  17.             level[rear]=k+1;
  18.         }
  19.         if(p->rchild){
  20.             Q[++rear]=p->lchild;
  21.             level[rear]=k+1;
  22.         }
  23.     }//while
  24.     //遍历结束后,rear+1为结点数
  25.     int max=0;
  26.     int i=0;
  27.     k=1;
  28.     while(i<=rear){
  29.         n=0;//记录每一层的结点数
  30.         while(i<=rear&&level[i]==k){
  31.             n++;
  32.             i++;
  33.         }
  34.         k=level[i];//更新层数
  35.         if(n>max)
  36.             max=n;
  37.     }//while
  38.     return max;
  39. }
  40. //改进,不使用level数组,一边遍历一边统计
  41. int BtWidth(BiTree T){
  42.     if(!T)
  43.         return 0;
  44.     BiTree *Q[maxsize];
  45.     front=rear=-1;
  46.     int last=1;//记录最右边结点在队列中位置
  47.     int wid=0;//记录局部宽度
  48.     int maxwidth=0;//记录最大宽度
  49.     Q[++rear]=T;
  50.     while(front<rear){
  51.         p=Q[++front];
  52.         wid++;
  53.         if(p->lchild)
  54.             Q[++rear]=p->lchild;
  55.         if(p->rchild)
  56.             Q[++rear]=p->rchild;
  57.         if(front>last){
  58.             last=rear;//last指向下一层最右边元素
  59.             if(wid>maxwidth)
  60.                 maxwidth=wid;
  61.             wid=0;
  62.         }//if
  63.     }//while
  64.     return maxwidth;
  65. }

4.假设二叉树采用二叉链存储结构存储，试设计一个算法，计算一棵给定二叉树的所有节点数。

  1. //递归
  2. int Nodes(BTNode *bt){
  3.     int left,right;
  4.     if(!bt)
  5.         return 0
  6.     else{
  7.         left=Nodes(bt->lchild);
  8.         right=Nodes(bt->rchild);
  9.         return (left+right+1);
  10.     }
  11. }

5.假设二叉树采用二叉链存储结构存储，设计一个算法计算一棵给定二叉树的所有叶子节点个数。

  1. //递归
  2. int leafNodes(BiTNode *bt){
  3.     int m,n;
  4.     if(!bt)
  5.         return 0;
  6.     else if(bt->lchild==NULL&&bt->rchild==NULL)
  7.         return 1;
  8.     else{
  9.         m=leafNodes(bt->lchild);
  10.         n=leafNodes(bt->rchild);
  11.         return m+n;
  12.     }
  13. }

6.假设二叉树采用二叉链存储结构存储，设计一个算法计算一棵给定二叉树的所有双分支节点。

  1. //递归
  2. int doubleNodes(BiTNode *bt){
  3.     int left,right,n;
  4.     if(!bt)
  5.         return 0;
  6.     else if(bt->lchild==NULL||bt->rchild==NULL)
  7.         n=0;
  8.     else
  9.         n=1;
  10.     left=doubleNodes(bt->lchild);
  11.     right=doubleNodes(bt->rchild);
  12.     return (left+right+n);
  13. }

7.假设二叉树采用二叉链存储结构存储，所有节点的值为正整数，设计一个算法求所有节点值之和。

  1. //递归
  2. int Findsum(BiTNode *bt){
  3.     if(!bt)
  4.         return 0;
  5.     else
  6.         return (bt->data+Findsum(bt->lchild)+Findsum(bt->rchild));
  7. }

8.假设二叉树采用二叉链存储结构存储，设计一个算法求其中节点值为 x的节点个数。 

  1. //递归
  2. int count_x(BiTNode *bt,ElemType x){
  3.     if(!bt)
  4.         return 0;
  5.     else if(bt->data==x)
  6.         return (1+count_x(bt->lchild,x)+count_x(bt->rchild,x));
  7.     else
  8.         return (count_x(bt->lchild,x)+count_x(bt->rchild,x));
  13.         )

9 假设二叉树采用二叉链表结构存储，设计一个算法求先序遍历序列中第k（1<=k<=二叉树中节点个数）个节点的值。

  1. int n=1;//标记结点序号
  2. ElemType PreNode(BiTNode *bt,int k){
  3.     ElemType ch;
  4.     if(bt==NULL)
  5.         return '';
  6.     if(n==k)
  7.         return bt->data;
  8.     n++;
  9.     ch=PreNode(bt->lchild,k);//遍历左子树
  10.     if(ch!='')
  11.         return ch;
  12.     ch=PreNode(bt->rchild,k);
  13.     return ch;
  14. }

10.假设二叉树采用二叉链存储结构存储，设计一个算法，求中序遍历序列中第k(1≤k≤二叉树中节点个数)个节点的值。

  1. int n=1;
  2. ElemType InOrder(BiTNode *bt,int k){
  3.     ElemType ch;
  4.     if(bt==NULL)
  5.         return '';
  6.     ch=InOrder(bt->lchild,k);
  7.     if(ch!='')
  8.         return ch;
  9.     else{
  10.         if(n==k)
  11.             return bt->data;
  12.         n++;
  13.         ch=InOrder(bt->rchild,k);
  14.         return ch;
  15.     }
  16. }

11.假设二叉树采用二叉链存储结构存储，设计一个算法，求后序遍历序列中第k(1≤k≤二叉树中节点个数)个节点的值。

  1. int n=1;
  2. ElemType PostOrder(BiTNode *bt,int k){
  3.     ElemType ch;
  4.     if(bt==NULL)
  5.         return '';
  6.     ch=PostOrder(bt->rchild,k);
  7.     if(ch!='')
  8.         return ch;
  9.     else{
  10.         ch=PostOrder(bt->lchild,k);
  11.         if(ch!='')
  12.             return ch;
  13.         if(n==k)
  14.             return bt->data;
  15.         n++;
  16.     }
  17. }

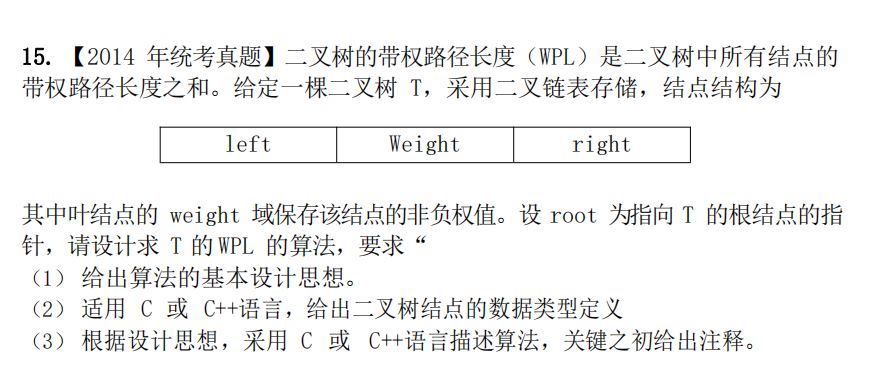
捕获.JPG

  1. int wpl_PreOrder(BiTree root,int deep){
  2.     static int wpl=0;
  3.     if(root->lchild==NULL&&root->rchild==NULL)
  4.         wpl=wpl+deep*root->weight;//叶子结点
  5.     if(root->lchild!=NULL)
  6.         wpl_PreOrder(root->left,deep+1);
  7.     if(root->right!=NULL)
  8.         wpl_PreOrder(root->rchild,deep+1);
  9.     return wpl;
  10. }

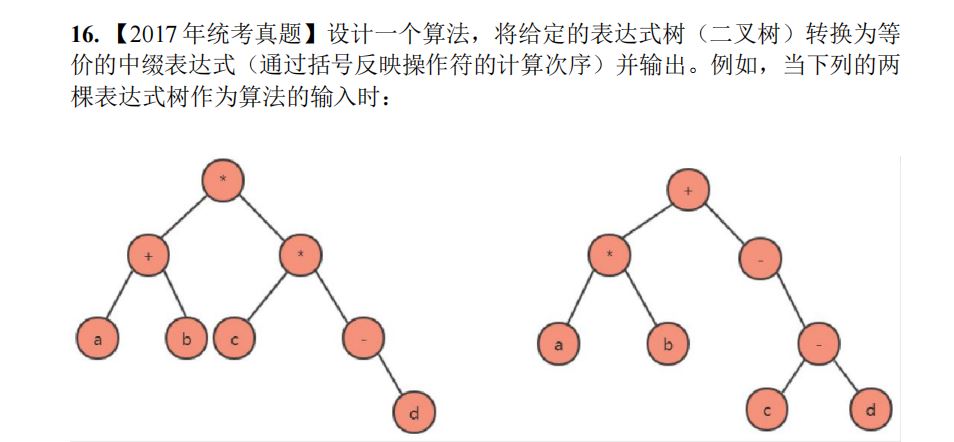
捕获.JPG

  1. typedef struct node{
  2.     char data[maxsize];
  3.     struct node *left,*right;
  4. }BiTree;
  5. void BiTreeToExp(BiTree *bt,int deep){
  6.     if(bt==NULL)
  7.         return ;
  8.     else if(bt->left==NULL&&bt->right==NULL)//叶子结点
  9.         printf("%s",bt->data);
  10.     else{
  11.         if(deep>1)
  12.             printf("(");
  13.         BiTreeToExp(bt->left,deep+1);
  14.         printf("%s",bt->data);
  15.         BiTreeToExp(bt->right,deep+1);
  16.         if(deep>1)
  17.             printf(")");
  18.     }
  19. }

17.判断一个树是否是完全二叉树

  1. typedef struct BiTNode{
  2.     ElemType data[maxsize];
  3.     struct BiTNode *lchild,*rchild;
  4. }
  5. typedef struct Queue{
  6.     BiTNode *data[maxsize];
  7.     int front,rear;
  8. }
  9. bool isCompleteBiTNode(BiTNode *bt){
  10.     Queue Q;
  11.     InitQueue(Q);
  12.     if(bt==NULL)
  13.         return true;
  14.     EnQueue(Q,bt);
  15.     int tag=0;//判断前面是否有空结点的标志位
  16.     while(!isEmpty(Q)){
  17.         BiTNode p;
  18.         DeQueue(Q,p);
  19.         if(p->lchild&&!tag)
  20.             EnQueue(Q,p->lchild);
  21.         else{
  22.             if(p->lchild)
  23.                 return false;
  24.             else
  25.                 tag=1;//首次出现非空结点
  26.         }
  27.         if(p->rchild&&!tag)
  28.             EnQueue(Q,p->rchild);
  29.         else{
  30.             if(p->rchild)
  31.                 return false;
  32.             else
  33.                 tag=1;
  34.         }
  35.     }
  36.     return true;
  37. }