排序算法的稳定性及汇总

image.png稳定性举例：
一个数组：arr = [1,2,3,2,3,1,2,2];
拍完序 arr = [1,1,2,2,2,2,3,3] 不仅保证顺序正确，还要保证索引顺序也正确；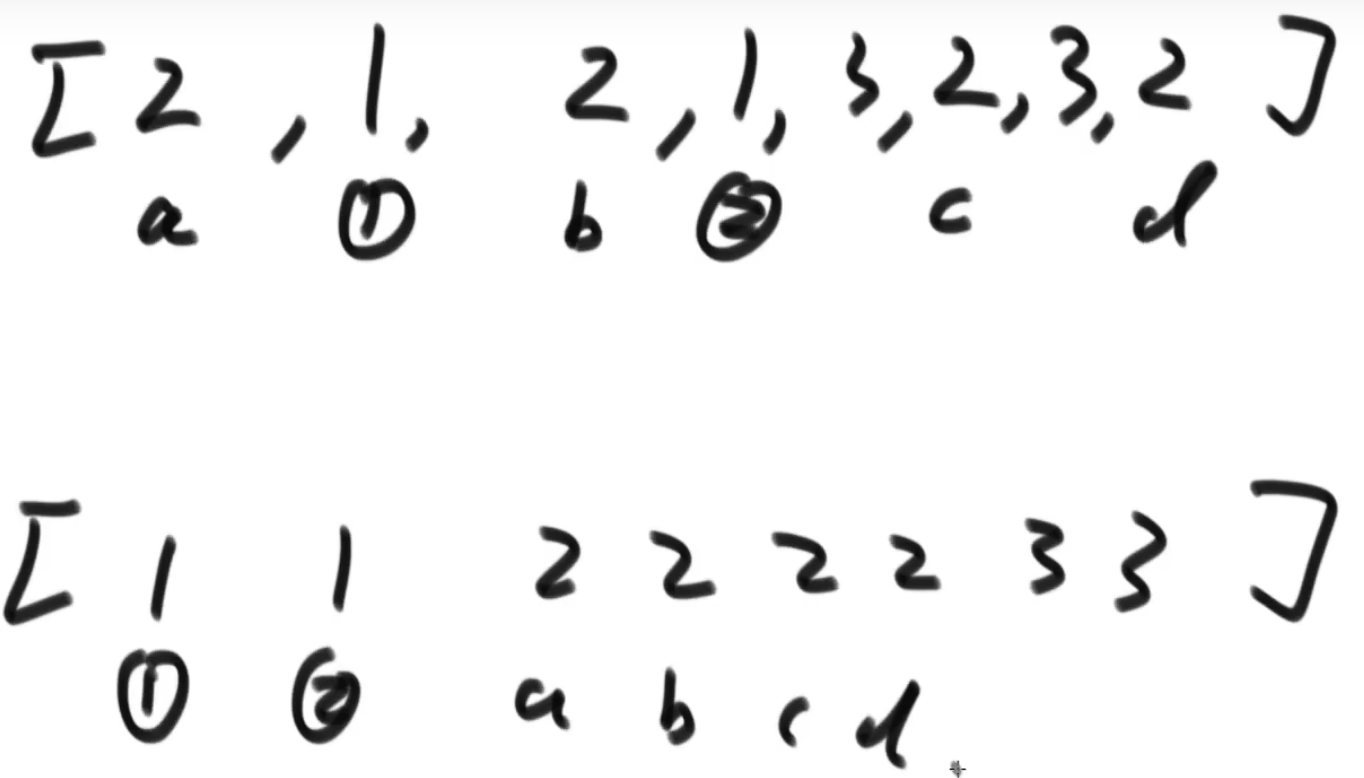
image.png
作用：
对基础类型没什么用，对非基础类型（我们实际生活中的一些）排序有很重要的作用。
比如：你先按价格低到高稳定排序，再按好评由好到差排序，那结果就是物美价廉的商品，排在最前面了。

不具备稳定性的排序：

1选择排序（n2）：
如【3，,3，,3，1，,3，,3，,3】
从左到右找到一个最小的跟第一个值“交换”，1和3交换以后，索引为0的3跑到了索引为1，,2的后面了，所以不
具备稳定性。

2快速排序（）：
3堆排序：

具备稳定性的排序：

1冒泡排序（n2）：（相等时不交换可以稳定，交换就会不稳定）
image.png

2 插入排序（n2）（相等时不交换可以稳定，否则不稳定）
image.png
右边的和左边的依次比较，比左边的小，就交换，插在左边，相等不交换就稳定

3归并排序（nlog(n)）:
image.png
merge的时候先拷贝左边的在拷贝右边的就能稳定

4计数排序（放桶，先入通的先出）
5基数排序（放桶，先入通的先出）

总结：
image.png

快排 指的是 随机快排，也叫 快排3.0

tips：1，一般来讲，排序的话会选择 “快排”，因为1，快排的指标（时间复杂度）是N*logN的，其次，经过实验的结果，快排的常数项是最低的，最快的，所以能用快排就用快排。
2，如果实在有空间的显示，很容易空间就超了，那就用 “堆排”。
3，如果需要使用有稳定性的排序，用归并排序
结论：根据不同需求使用不同排序，目前来说不能达到完美的排序，时间复杂度，空间复杂度也低，还稳定，要有取舍的

image.png
image.png
O(N*logN)利用其调度的优势， O(N^2)利用小样本情况下常数时间低的优势

系统自己实现的排序：如果发现你的数组是基础类型的，就用快排，否则用归并，请问为什么？ 是因为 稳定性。

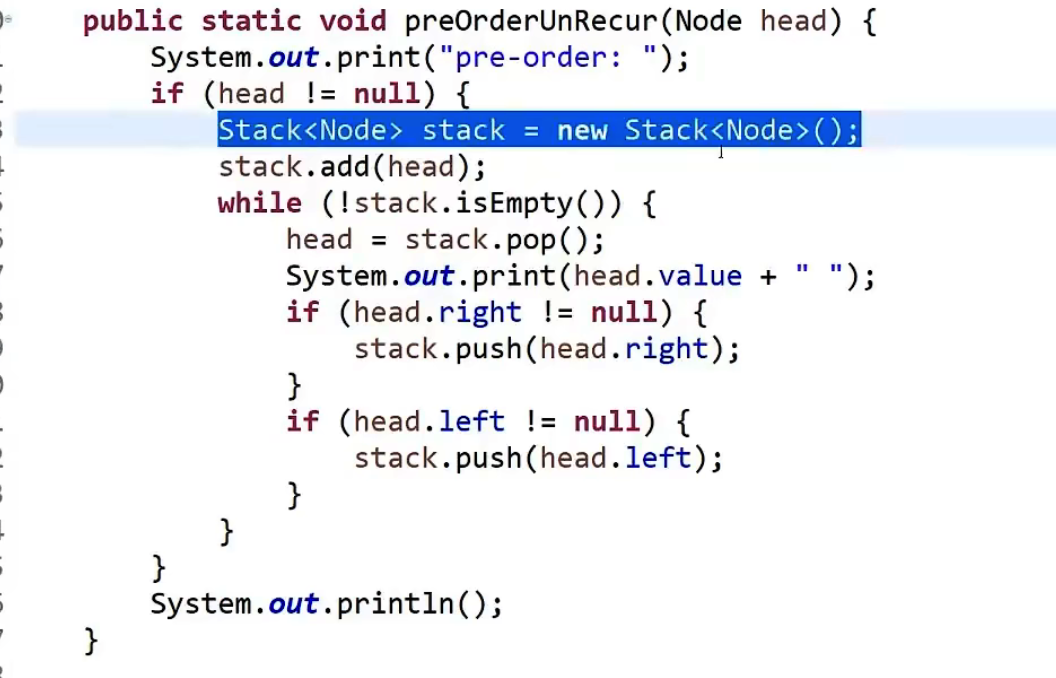
image.png

先序遍历：（非递归）
image.png