go-zero高可用-分布式布隆过滤器（Bloom Filter）

为什么需要布隆过滤器

想象一下遇到下面的场景你会如何处理：

1. 手机号是否重复注册
2. 用户是否参与过某秒杀活动
3. 伪造请求大量id查询不存在的记录，此时缓存未命中,如何避免缓存穿透

针对以上问常规做法是：查询数据库，数据库硬扛，如果压力并不大可以使用此方法，保持简单即可。

改进做法：用list/set/tree维护一个元素集合，判断元素是否在集合内，时间复杂度或空间复杂度会比较高。如果是微服务的话可以用redis中的list/set数据结构, 数据规模非常大此方案的内存容量要求可能会非常高。

这些场景有个共同点，可以将问题抽象为：如何高效判断一个元素不在集合中？
那么有没有一种更好方案能达到时间复杂度和空间复杂双优呢？
有！布隆过滤器。

什么是布隆过滤器

布隆过滤器（英语：Bloom Filter）是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中，它的优点是空间效率和查询时间都远远超过一般的算法。

工作原理

布隆过滤器的原理是，当一个元素被加入集合时，通过K个散列函数将这个元素映射成一个位数组中的K个点（offset），把它们置为1。检索时，我们只要看看这些点是不是都是1就（大约）知道集合中有没有它了：如果这些点有任何一个0，则被检元素一定不在；如果都是1，则被检元素很可能在。这就是布隆过滤器的基本思想。

简单来说就是准备一个长度为m的位数组并初始化所有元素为0，用k个散列函数对元素进行k次散列运算跟len(m)取余得到k个位置并将m中对应位置设置为1。

布隆过滤器优缺点

优点：

1. 空间占用极小，因为本身不存储数据而是用比特位表示数据是否存在，某种程度有保密的效果。
2. 插入与查询时间复杂度均为O(k)，常数级别，k表示散列函数执行次数。
3. 散列函数之间可以相互独立，可以在硬件指令层加速计算。

缺点：

1. 误差（假阳性率）。
2. 无法删除。

   误差（假阳性率）

布隆过滤器可以100%判断元素不在集合中，但是当元素在集合中时可能存在误判，因为当元素非常多时散列函数产生的k位点可能会重复。
维基百科有关于假阳性率的数学推导（见文末链接）这里我们直接给结论(实际上是我没看懂…)，假设：

• 位数组长度m
• 散列函数个数k
• 预期元素数量n
• 期望误差ε

在创建布隆过滤器时我们为了找到合适的m和k，可以根据预期元素数量n与_ε_来推导出最合适的m与k。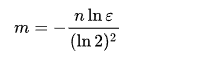

java中Guava,Redisson实现布隆过滤器估算最优m和k采用的就是此算法：

  //计算哈希次数
  @VisibleForTesting
  static int optimalNumOfHashFunctions(long n, long m) {
    // (m / n) * log(2), but avoid truncation due to division!
    return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
  }
//计算位数组长度
  @VisibleForTesting
  static long optimalNumOfBits(long n, double p) {
    if (p == 0) {
      p = Double.MIN_VALUE;
    }
    return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
  }

无法删除

位数组中的某些k点是多个元素重复使用的，假如我们将其中一个元素的k点全部置为0则直接就会影响其他元素。
这导致我们在使用布隆过滤器时无法处理元素被删除的场景。
可以通过定时重建的方式清除脏数据。假如是通过redis来实现的话重建时不要直接删除原有的key，而是先生成好新的再通过rename命令即可，再删除旧数据即可。

go-zero中的bloom filter源码分析

core/bloom/bloom.go

一个布隆过滤器具备两个核心属性：

1. 位数组：
2. 散列函数

go-zero实现的bloom filter中位数组采用的是Redis.bitmap，既然采用的是redis自然就支持分布式场景，散列函数采用的是MurmurHash3

Redis.bitmap为什么可以作为位数组呢？

Redis中的并没有单独的bitmap数据结构，底层使用的是动态字符串（SDS）实现，而Redis中的字符串实际都是以二进制存储的。
a 的ASCII码是 97，转换为二进制是：01100001，如果我们要将其转换为b只需要进一位即可：01100010。下面通过Redis.setbit实现这个操作：

set foo a
OK
get foo
“a”
setbit foo 6 1
0
setbit foo 7 0
1
get foo
“b”

bitmap底层使用的动态字符串可以实现动态扩容，当offset到高位时其他位置bitmap将会自动补0，最大支持232-1长度的位数组（占用内存512M），需要注意的是分配大内存会阻塞Redis进程。
根据上面的算法原理可以直到实现布隆过滤器主要做三件事情：

1. k次散列函数计算出k个位点。
2. 插入时将位数组中k个位点的值设置为1。
3. 查询时根据1的计算结果判断k位点是否全部为1，否则表示该元素一定不存在。

下面来看看go-zero是如何实现的：

对象定义

//表示经过多少散列函数计算
//固定14次
maps = 14
type (
    // 定义布隆过滤器结构体
    Filter struct {
        bits   uint
        bitSet bitSetProvider
    }
    //位数组操作接口定义
    bitSetProvider interface {
        check([]uint) (bool, error)
        set([]uint) error
    }
)

位数组操作接口实现

首先需要理解两段lua脚本：

//ARGV:偏移量offset数组
//KYES[1]: setbit操作的key
//全部设置为1
setScript = `
    for _, offset in ipairs(ARGV) do
        redis.call("setbit", KEYS[1], offset, 1)
    end
    `
//ARGV:偏移量offset数组
//KYES[1]: setbit操作的key
//检查是否全部为1
testScript = `
    for _, offset in ipairs(ARGV) do
        if tonumber(redis.call("getbit", KEYS[1], offset)) == 0 then
            return false
        end
    end
    return true
    `

为什么一定要用lua脚本呢?
因为需要保证整个操作是原子性执行的。

//redis位数组
type redisBitSet struct {
    store *redis.Client
    key   string
    bits  uint
}
//检查偏移量offset数组是否全部为1
//是:元素可能存在
//否:元素一定不存在
func (r *redisBitSet) check(offsets []uint) (bool, error) {
    args, err := r.buildOffsetArgs(offsets)
    if err != nil {
        return false, err
    }
    //执行脚本
    resp, err := r.store.Eval(testScript, []string{r.key}, args)
    //这里需要注意一下,底层使用的go-redis
    //redis.Nil表示key不存在的情况需特殊判断
    if err == redis.Nil {
        return false, nil
    } else if err != nil {
        return false, err
    }
    exists, ok := resp.(int64)
    if !ok {
        return false, nil
    }
    return exists == 1, nil
}
//将k位点全部设置为1
func (r *redisBitSet) set(offsets []uint) error {
    args, err := r.buildOffsetArgs(offsets)
    if err != nil {
        return err
    }
    _, err = r.store.Eval(setScript, []string{r.key}, args)
    //底层使用的是go-redis,redis.Nil表示操作的key不存在
    //需要针对key不存在的情况特殊判断
    if err == redis.Nil {
        return nil
    } else if err != nil {
        return err
    }
    return nil
}
//构建偏移量offset字符串数组,因为go-redis执行lua脚本时参数定义为[]stringy
//因此需要转换一下
func (r *redisBitSet) buildOffsetArgs(offsets []uint) ([]string, error) {
    var args []string
    for _, offset := range offsets {
        if offset >= r.bits {
            return nil, ErrTooLargeOffset
        }
        args = append(args, strconv.FormatUint(uint64(offset), 10))
    }
    return args, nil
}
//删除
func (r *redisBitSet) del() error {
    _, err := r.store.Del(r.key)
    return err
}
//自动过期
func (r *redisBitSet) expire(seconds int) error {
    return r.store.Expire(r.key, seconds)
}
func newRedisBitSet(store *redis.Client, key string, bits uint) *redisBitSet {
    return &redisBitSet{
        store: store,
        key:   key,
        bits:  bits,
    }
}

到这里位数组操作就全部实现了，接下来看下如何通过k个散列函数计算出k个位点

k次散列计算出k个位点

//k次散列计算出k个offset
func (f *Filter) getLocations(data []byte) []uint {
    //创建指定容量的切片
    locations := make([]uint, maps)
    //maps表示k值,作者定义为了常量:14
    for i := uint(0); i < maps; i++ {
        //哈希计算,使用的是"MurmurHash3"算法,并每次追加一个固定的i字节进行计算
        hashValue := hash.Hash(append(data, byte(i)))
        //取下标offset
        locations[i] = uint(hashValue % uint64(f.bits))
    }
    return locations
}

插入与查询

添加与查询实现就非常简单了，组合一下上面的函数就行。

//添加元素
func (f *Filter) Add(data []byte) error {
    locations := f.getLocations(data)
    return f.bitSet.set(locations)
}
//检查是否存在
func (f *Filter) Exists(data []byte) (bool, error) {
    locations := f.getLocations(data)
    isSet, err := f.bitSet.check(locations)
    if err != nil {
        return false, err
    }
    if !isSet {
        return false, nil
    }
    return true, nil
}

改进建议

整体实现非常简洁高效，那么有没有改进的空间呢？
个人认为还是有的，上面提到过自动计算最优m与k的数学公式，如果创建参数改为：
预期总数量expectedInsertions
期望误差falseProbability
就更好了，虽然作者注释里特别提到了误差说明，但是实际上作为很多开发者对位数组长度并不敏感，无法直观知道bits传多少预期误差会是多少。

// New create a Filter, store is the backed redis, key is the key for the bloom filter,
// bits is how many bits will be used, maps is how many hashes for each addition.
// best practices:
// elements - means how many actual elements
// when maps = 14, formula: 0.7*(bits/maps), bits = 20*elements, the error rate is 0.000067 < 1e-4
// for detailed error rate table, see http://pages.cs.wisc.edu/~cao/papers/summary-cache/node8.html
func New(store *redis.Redis, key string, bits uint) *Filter {
    return &Filter{
        bits:   bits,
        bitSet: newRedisBitSet(store, key, bits),
    }
}
//expectedInsertions - 预期总数量
//falseProbability - 预期误差
//这里也可以改为option模式不会破坏原有的兼容性
func NewFilter(store *redis.Redis, key string, expectedInsertions uint, falseProbability float64) *Filter {
    bits := optimalNumOfBits(expectedInsertions, falseProbability)
    k := optimalNumOfHashFunctions(bits, expectedInsertions)
    return &Filter{
        bits:   bits,
        bitSet: newRedisBitSet(store, key, bits),
        k:      k,
    }
}
//计算最优哈希次数
func optimalNumOfHashFunctions(m, n uint) uint {
    return uint(math.Round(float64(m) / float64(n) * math.Log(2)))
}
//计算最优数组长度
func optimalNumOfBits(n uint, p float64) uint {
    return uint(float64(-n) * math.Log(p) / (math.Log(2) * math.Log(2)))
}

资料

布隆过滤器（Bloom Filter）原理及Guava中的具体实现

布隆过滤器-维基百科

Redis.setbit