对simhash的简单理解 - 知乎

-1 为什么这么长

我整理这个文档的最初目的是将 simhash 的基本原理搞清楚，这个初心在学习的过程中逐渐改变了。

在整理和学习 simhash 相关资料的过程中，我不理解 simhash 得到的文本特征有效性的来源，于是开始了解 simhash 所属的局部敏感哈希，尝试找到解释。从论文和大家的博客来看，随机投影 hash 和随机超平面 hash 局部敏感哈希的经典形式。于是，我盯着这两个 “随机” 朋友看了很久。当了解到随机投影是一种数据降维方法的时候，我终于相信这两个 hash 算法区别不是特别大。

为了记录 simhash 相关知识内容，也为了记录自己在知识地图中搜索的过程，我搞了一个新花样——大杂烩。新花样总的来说会让人的大脑分泌一些带来快乐的东西，然后露出如图 - 1-1 的表情。这也是强化自己的学习动力的一种方式。

图 - 1 -1 当手下又有鬼点子时

本文的目录如图 - 1-2。

图 - 1-2 目录

0 引言

21 世纪不是生物的世纪，而是数据的世纪。数据已经成为我们这个文明必不可少的一部分，不管走到哪里，我们都沐浴在数据形成的空气中。现在，这种空气有点太多，大家快要氧中毒了——互联网、工业生产等领域产生的数据太多，我们在管理和使用这些数据时遇到了几种困难：高维度、极大的数量、重复问题。我们需要使用包括 simhash 在内的算法来解决这些问题。

0.1 我要降维

随着采集能力和存储能力的强大，我们得了贪食症，不管一个字段是否有用，先存起来再说。总的来说，字段越多，我们可以构造的特征就越多、可以输入模型的信息就越多。不过呢，特征多是有代价的，它会降低模型的训练和计算速度。但是，我比较贪心，就是要马儿不吃草、还跑得快：在特征数量较小的情况下，尽量多地向模型提供信息。

那只能降维了。

0.2 我要搜索

采集和存储能力的强大，也让我们的数据积累了海量的文档、“啥都有”。但是，如果没有较强的检索能力，“海量数据”就是 “啥都找不到”“啥都没有” 的代名词。

我们需要强有力的搜索技术。

0.3 我需要去重

很多情况下，我们需要对文本数据进行去重：当文本分类语料有重复的样本；有些网站会将同一片文章重复发若干次，导致我们采集到大量重复的内容，进而影响后续热点检测等任务的效果；等等。

假如有 10 篇文档需要去重，我可以亲自上、手工排重。这个任务几十秒钟就完成了。

假如有 10000 篇文档需要去重，可以使用适当的相似度算法判断是否重复，然后用 single-pass 的框架对文档进行聚类 ，最后保留所有簇的中心文档即可。这种算法最多需要计算大约（1+9999）*10000/2 次相似度，耗时会很久。当然了，我们可以用一个倒排索引来加速。

假如我们有 100000000 篇文档需要去重，按我以前的套路，就是用 Spark 这样的工具咔咔算，算到天荒地老。不过呢，如果我们使用合适的文本相似度算法和倒排索引的构建方法，用一台内存足够的机器，可以在有生之年完成这个任务。

我需要一个高效的文本去重算法。

0.4 我要局部敏感哈希

前面所说的几个需求，我们可以用很多方法来满足。可选的方案中，有一朵奇葩，那就是局部敏感哈希 (Local Sensitive Hash)。LSH 的思想是，在保留数据相对位置的条件下，将原始数据映射到一个碰撞率较高的低维的新空间里，从而降低下游任务的计算量。利用局部敏感哈希编码的高碰撞率，我们可以设计出更加稀疏的倒查索引键值，从而得到非常高效的文本去重方案，即基于 simhash 的文本去重方法。

如图 0-1，是我在整理 simhash 相关的内容时，探索出来的知识地图，算是本文的另一种目录。

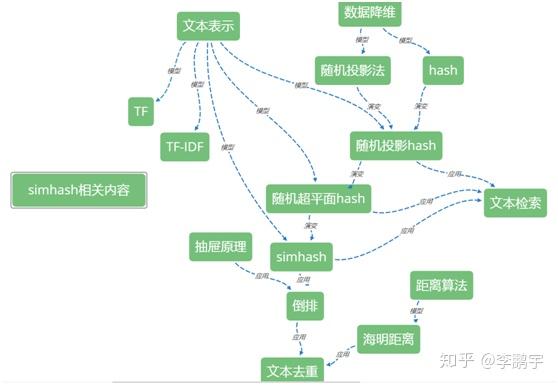
图 0-1 已探明的知识地图

1 从基于随机投影的数据降维说起

1.1 向量点积的含义

随机投影的基础方法，是向量点积运算。而理解随机投影的基础，是理解向量点积运算的含义。如图 1-1，二维平面中有两个向量

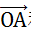
和

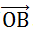
。二者的点积为:

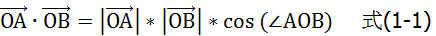
一般来说，我们会把向量点积理解为，计算向量夹角时的中间结果。

这里，为了帮助理解随机投影，需要重新解释一下。向量点积表示的是，向量

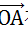
在向量

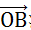
法平面上投影长度的加权值，其中权重为

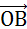
的长度 (当然由于乘法可交换，这里两个向量可以互换)。得到的投影向量为:

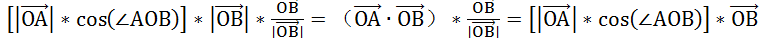
如果我们将

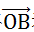
看做一个新空间的坐标轴，那么，在新的空间中，点 A 的坐标就是

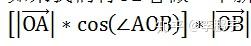
这样，我们就用向量

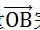
完成了对点 A 的映射。

举个例子，假设两个向量:

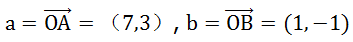
那么 a.b=71+3(-1)=4。点 A 以

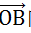
向量所在直线为坐标轴的空间中，坐标是 4。

注意，经过这通操作，点 A(在新空间中) 的坐标由 2 维降到了 1 维。

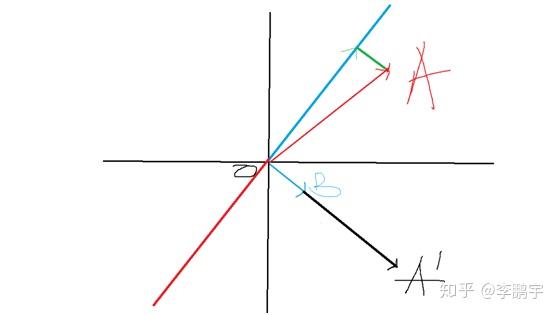
图 1-1 向量点积的含义

1.2 基于随机投影的降维——2 维到 1 维

Johnson–Lindenstrauss 引理指出，在欧式空间中的若干点，经过相同的映射后进入新的空间，它们仍然会保持原来的相对位置。简单来说，“相对位置”指的是一些点相距较近，一些点相距较远。这里只从直觉上展示随机投影 “保留数据相对位置” 的性质。具体的证明暂时就免了。

假设二维平面中，有若干点 A=(7,3), C=(-0.5,-1.5),D=(9,2),E=(-0.5,2.5)。目测，A 和 D 离得比较近；C 和 E 里的比较近。

我们使用向量

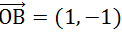
，将这 4 个点映射到新的空间，坐标分别是 A1=4，C1=1,D1=7,E1=-3。A1 和 D1 里的比较近；C1 和 E1 离得比较近；当然了，C1 和 D1 也挺近的。这样，二维坐标系里的 4 个点，被映射到了一个 1 维空间中，还在一定程度上保留了原来的相对位置。

那么，

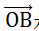
是怎么来的呢？随机生成。我们可以基于高斯分布，生成 B 点的横坐标和纵坐标。为啥是高斯分布呢？有一定的原因，这里暂时无力讲述。

这可省事了，我们在原始数据所属的空间中，随机生成一个向量，就可以基于这个向量，将原始数据映射到一个 1 维空间中。不过呢，在新空间中，数据点之间的相对距离存在一定程度的失真，怎么办呢？

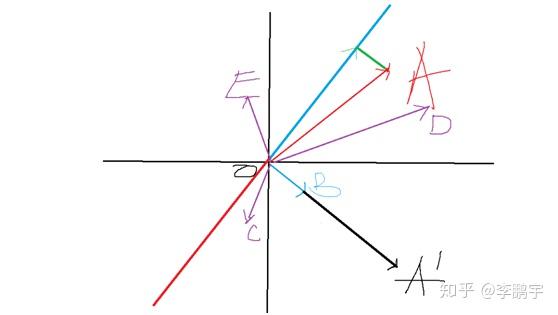
图 1-2 二维平面里的几个点

1.3 随机投影的降维——N 维到 K 维

假设有 M 条数据，维度非常高，为 N。随机投影法将帮我们把这种数据压缩为 K 维 (K 远小于 N)。

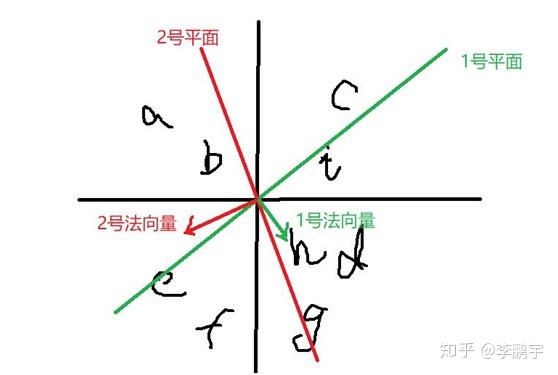
图 1-1 二维平面上的原始数据向量和随机向量

将原始数据看做高维空间中的一个点。那么对应第 m 条数据，有一个向量

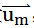
，从原点出发到这个数据点。

我们随机生成 K(K 远小于 N) 个长度为 N 的一维向量

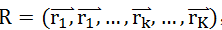
，将原始数据映射到以这些随机向量所在直线为坐标轴的新空间中，得到点

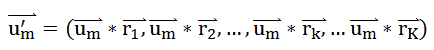
。这种降维方法叫做 “随机投影法”。总的来说，K 越大，降维后的数据，保留的信息越多，数据之间的相对位置越 “保真”——可以证明，但是这里无力搞了。

1.4 随机投影法降维的 python 实现

github 地址：

https://github.com/lipengyuer/DataScience/blob/master/src/algoritm/RandomProjectionDimReduction.pygithub.com

2 随机投影与局部敏感哈希

2.1 随机投影降维的简化——基于随机投影的局部敏感哈希

在 1.3 中提到，随机投影法可以把高维数据映射到新的空间中。由于特征维度大大降低了，聚类、分类、搜索等任务的计算量也大大降低了。不过呢，人心不足蛇吞象，我还想进一步降低计算量。

新的空间里，坐标轴还是实数轴，降维后的特征是连续特征。有人认为，这样的话还得用 float 这种类型存储数据、还得进行 float*float 的操作，浪费。有些高手本着如图 2-1 的原则，对随机投影降维进行了改进。

图 2-1 工程师的追求

在将数据映射到新空间后，我们将落在坐标轴负轴的维度 (该维度取值为负数)，统一赋值为 0，表示数据与对应随机向量夹角大于 90 度。或者说，数据点与随机向量，在以后者为法向量、过原点的超平面的同侧。类似的，我们将落在坐标轴非负轴的维度，统一赋值为 1。这样原始数据就被映射到了一个离散的新空间里。

这里所述的数据映射方法，就是我们常说的基于随机投影的局部敏感哈希。局部敏感哈希，与常见的 hash 有啥关系呢？局部敏感哈希是 hash 算法的一种，是数据映射方法，通常被用来对数据进行降维。

2.2 黑白分明的 hash

一般来说，我们遇到的数据长度 n 是可变的。我们可以用 hash 函数，将数据映射为一个长度固定为 K(K 远小于 n) 的编码。Hash 函数的输出，是对原始数据的一种压缩表示，也叫做数字签名、数字指纹、消息摘要或者散列值。常见的 hash 算法非常严格，要求碰撞率尽量低，即每条数据拥有一个唯一的 id。

从 hash 的原理来看，内容相同的文档，具有相同的哈希码；内容略有不同的文档，对应的哈希码会有很大的不同。如表 2-1，是一些句子的 hash 值。其中句子 1 和 3 的哈希码相等；句子 1 和句子 4 只差了一个字，哈希码具有肉眼可见的巨大差异。

Hash 码可以用来判断两个字符串是否相等。这样做有什么意义呢？我们把文档的哈希码存储起来，当需要判断两篇文档是否相等时，直接判断二者的哈希码即可。如果文档比较长 (几百字)，而哈希码比较短 (几十位)，那么后者的相等判断是比较快的。如果说，我们用位运算来进行哈希码的相等判断，那就更快了。因此，基于哈希码来判断文档内容是否相同，在一些场景里是非常高效的方案。

表 2-1 句子们和它们的 hash 编码

在信息检索任务中，我们可以为每一条记录生成一个 hash 码、作为 id，这样就可以为一篇文档快速地找到相关的字段了。然而，假如需要检索的是相似的文档，普通的 hash 算法就没办法了。这时候，我们需要不太严格的 hash 编码方法。

2.3 随机投影 hash 的用途

局部敏感哈希是非常适合文本数据检索场景的编码方法。 局部敏感哈希在随机投影降维方法的基础上，增加了离散化环节。这个 “离散” 有啥用呢？

直观地看，原来空间中的 - 0.66 和 - 100，在新空间都成为 1 或者 0, 也就是说，二者在新的空间中是相等的。这样的结果是，在原来空间中比较接近的数据点，在新的空间中，在一些维度上可能是相等的。

基于取值相同的维度，我们可以把数据分组 (俗称分到桶里)。在搜索文档的时候，我们对查询语句进行 hash，然后把各个维度上、桶的编号相同的文档召回，最后进行精排，可以实现快速而高质量的搜索。一个基于分桶构建的倒查索引可以帮助我们实现这样的操作。

一些在原来空间接近的数据点，经过这样的映射后，仍然相似甚至相等 (各个维度坐标都相等)。对二进制编码进行相似度计算是非常快速的，在这个基础上我们可以进行非常快速的聚类。

另外，我们可以把映射后相等的数据看做是相同的数据，进而进行排重。

2.4 随机超平面 hash

随机超平面 hash 是在随机投影 hash 的基础上发展而来的。二者的名称含义相近，就像算法内容一样。与随机投影 hash 的主要区别是，随机超平面 hash 的编码结果是 - 1 和 1 组成的串——与随机向量点积为负数，新空间中该维度取值 - 1；与随机向量点积为非负数，新空间中该维度取值为 1。

由于使用了新空间中所有象限，随机超平面 hash 的性能更好一些，在文本分类、聚类任务中表现更好。

2.5 两种局部敏感哈希的 python 实现

GitHub 地址:

https://github.com/lipengyuer/DataScience/blob/master/src/nlp/LSH/RandomProjectionLSH.pygithub.comhttps://github.com/lipengyuer/DataScience/blob/master/src/nlp/LSH/RandomHyperplaneLSH.pygithub.com

3 局部敏感哈希的杰出代表：simhash

“hash”是我们经常使用的一种对数据的映射操作，它会把特定类型的数据 (如字符串) 映射为另一种数据 (比如内存地址)。“simhash” 是一种将文本数据映射为固定长度的二进制编码的算法。当然了，由于基于 simhash 的文本相似度计算方法、文本去重方法名气比较大，大家经常以 “simhash” 代指 “基于 simhash 编码的文本相似度计算方法” 或者“基于 simhash 编码表示的文本去重方法”。这样混乱的称呼，特别容易引起混淆，因此这里约定几个提法：（1）simhash 是一种将文本数据映射为定长二进制编码的 hash 算法，用 NLP 的说法就是一种文本表示模型 ；（2）基于 simhash 的文本相似度计算，就是用文本的 simhash 值作为特征向量，来计算文档之间的相似度或者距离；（3）基于 simhash 的文本去重，就是使用基于 simhash 表示来计算文本相似度，进而发现重复文档并删除。

3.1 历史选择了 simhash

在文本分类、聚类、相似度计算等等任务中，我们希望用一个定长的数值向量表示文本。这样我们才能用欧氏距离等方法计算文本的相似度。常见的文本表示模型有 TF(Term Frequency)、TF-IDF（Term Frequency-Inverse Document Frequency）、句向量等等。

在海量文本去重场景下，上述几种模型都有一些不足:

（1）TF 精度较差, 即对 “非常相似” 到“相同”这个相似度范围的判断不是很敏感；受文本长度等因素影响较大，相似度阈值定起来比较麻烦。

(2) 精度也比较差； TF-IDF 要求首先遍历一遍所有文本来的得到 IDF，计算量比较大；

(3) 句向量主要关注的是语义，对字面的相似不太擅长；计算量比较大。

而 simhash 克服了以上几种算法的不足。

3.2 从文本的词向量空间模型到 simhash

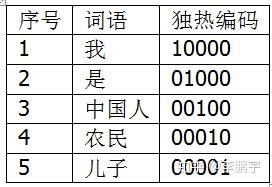
在词向量空间模型中，我们把词语映射为一个独热编码 (one-hot encoding)。假设词汇表为 (我，是，中国人，农民，儿子)，大小为 5，那么这几个词语的独热编码如表 3-1。将文本分词后，把词语的独热编码按位累加，就得到了 TF 向量。比如 “我是一个码农，是农民的儿子”，分词后得到 “我 / 是 / 一个 / 码农 /，/ 是 / 农民 / 的 / 儿子”，基于词语编码表，得到的 TF 向量就是 (1,2,0,1,1)。

表 3-1 词语的独热编码

高维度是 TF 的主要缺点。一般来说，我们的词汇是数以万计的，TF 向量会比较长，导致下游任务计算量比较大。比如计算两篇文本的欧氏距离，我们需要执行数万次的减法、平方、加法等。

为此，Simhash 从词语编码的降维入手，实现了对 TF 的降维。

3.3simhash 的计算过程

Simhash 是如何将文本映射为数值向量的呢？

首先，它基于 hash 算法将词语映射为较短的编码，然后使用随机超平面 hash 的做法得到最终的词语编码。然后，就像 TF 的计算一样，将每个词语的编码加起来。最后，采用随机超平面的离散化方法，得到文本的最终表示。

假设我们需要把 S=“我爱北京天安门” 这句话转换成长度为 5 的二进制编码。

3.3.1 分词

按照一定的粒度切分文本，比如分词。S 可以切分为” 我 / 爱 / 北京 / 天安门”.

3.3.2 将词语映射为定长二进制编码

将文本的每一个碎片，用一种 hash 算法映射为一定长度的二进制编码。如表 3-2，是我假想的几个词语的编码值。

表 3-2 S 的词语的 hash 值

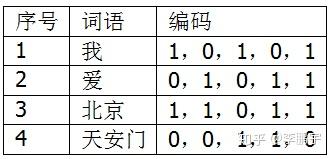
3.3.3 将词语的二进制编码再转换一下

我们需要把词语二进制编码中的 “0” 一律转换为“-1”，得到词语的最终编码，如表 3-3。将 0 转换为 - 1 的目的，是将映射后的词语放置在整个空间中，而不是某一个象限，这样可以让数据点分布得更均匀一点。

注意，TF 里，每个词语的权重比较粗暴，如果想升级一下，可以考虑 TF-IDF。

与随机超平面 hash 相比，这里使用了一个 “不随机” 的超平面，将空间进行了分割。

表 3-3 S 的词语的新编码

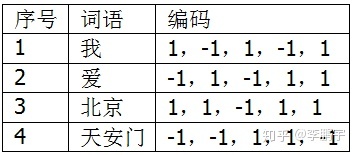
3.3.4 计算文档的初级编码

我们将句子中所有词语的编码加起来，就得到了句子的编码（0,0,0,2,2）。

3.3.5 计算文档的最终编码

将句子编码的非正数元素转换为 0，正数元素转换为 1，就得到了句子的最终编码 (0,0,0,1,1)——这就是句子的 simhash 编码。

3.4 基于 simhash 编码计算文本距离

Simhash 完成了文本的低纬度表示 ，接下来我们就可以进行文本相似度、文本分类等任务了。这里以文本相似度计算为例，展示 simhash 码的使用方式。

3.4.1 海明距离

海明距离是 simhash 的经典搭档，用来在 simhash 码的基础上度量文本之间的距离或相似度。假设有两个等长（长度为 K）的数据串：

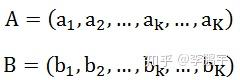
二者的海明距离等于:

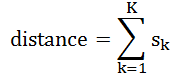
其中

假设文档 A 和文档 B 的 simhash 码分别为 (1,1,0,1) 和(1,0,0,1)，那么二者的海明距离就是 0+1+0+0=1（感谢

victor diaowww.zhihu.com

的提醒，之前这里是 “0+1+1+0=2”，是一个错误）。

海明距离的特点是，在实际应用中，只需要进行基本数据类型的相等判断和加法，计算速度非常快。

3.4.2 用位运算对 simhash 升级

Simhash 码是二进制编码，可以使用位运算来实现一些快速的操作。这是 simhash 高性能的一个重要来源。

3.5 基于 simhash 计算文本距离的 python 实现

github 地址是:

https://github.com/lipengyuer/DataScience/blob/master/src/nlp/LSH/simhash_v1.pygithub.comhttps://github.com/lipengyuer/DataScience/blob/master/src/nlp/LSH/simhash_v2.pygithub.com

4 基于 simhash 的文本去重框架

基于 simhash 的海量文本去重框架里同时涉及了搜索和聚类的关键技术，可以快速地修改为搜索和聚类工具。因此，这里用一个基于 simhash 的文本去重框架展示 simhash 的应用方式。

假设我们需要对 M 篇文档进行去重。

4.1 比较暴力的去重框架

最简单的方式，是计算每两篇文档之间的距离，然后对距离不超过 3 的文档对进行去重处理。这样的话，我们需要计算 (M-1+0)*M/2 词相似度，计算量非常大。

4.2 使用倒查索引优化去重框架

我们可以使用倒查索引来降低计算量。以 64 位 simhash 编码表示的数据集为例，我们可以构建 64 个倒查索引，对应 simhash 码的 64 个维度；每个倒查索引只有两个 key，即 0 和 1，表示文本编码在这个维度上的取值；这样，我们就可以把所有的文档，按照 simhash 编码在各维度上的取值，放到各个倒查索引中。

在实际去重的时候，每遍历到一个不重复的文档，就把它添加到 64 个倒查索引中。

在考察一篇文档是否重复的时候，我们首先把 64 个倒查索引中，与当前文档编码匹配的部分召回，然后比对当前文档与召回文档的相似度，进而判断是否重复。这种查询方式比 4.1 所述的方式，需要比对的次数要少很多。

当然，这种倒查索引的 key 还是比较稠密，每次查询会召回比较多的文档。

4.3 基于抽屉原理升级倒查索引

我们可以设计更稀疏的 key，来获得更高的查询精度，进而进一步减少召回的文档数量。

4.3.1 抽屉原理

我们可以用抽屉原理来对去重框架进行升级。

如图 4-1，有 3 个抽屉、4 个苹果。将 4 个苹果放到抽屉里，那么至少一个抽屉里，有 2 个苹果。当我们有 X 个抽屉、X+1 个苹果，可以得到同样的结论，至少有一个抽屉里有 2 个苹果。这就是抽屉原理。

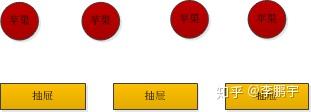
图 4-1 个苹果与 3 个抽屉

一般来说文本重复与否海明距离阈值是 3，当两篇文档被判定相似，那么二者的 simhash 码最多有 3 个位置是不相等的 (感谢

AndrewFuwww.zhihu.com

的提醒，原来是 “相等”，现已改正)。换句话说，如果两篇文档的 simhash 编码的海明距离小于等于 3，我们认为二者是相似的。假设我们的 simhash 编码是 64 位，可以分为 4 组连续的数字。那么两篇相似文档的 simhash 编码中，至少有一个子串是完全相等的。换句话说，只有包含了文档 A 的 4 个子串中的一个的文档，才有可能与 A 相似。

4.3.2 更稀疏的 key

我们可以把 simhash 码切分为 4 个 (数字可以变化) 连续的子串，然后以子串为 key 取构建倒排索引。这时候，倒查索引的数量降到了 4 个。每个字串是一个 16 位的二进制编码，命中的文档数量相比 4.2 所述 key 更少。结果就是，查询的时候，召回的文档数量更少了。

4.4 完整的去重框架

如图 4-2 和图 4-3，分别是向倒查索引添加文档，和召回文本并排重的框架。

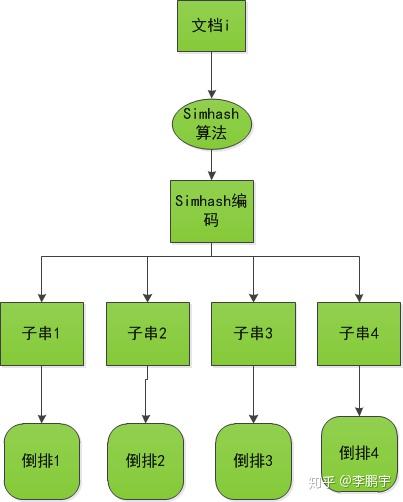
图 4-2 构建倒排

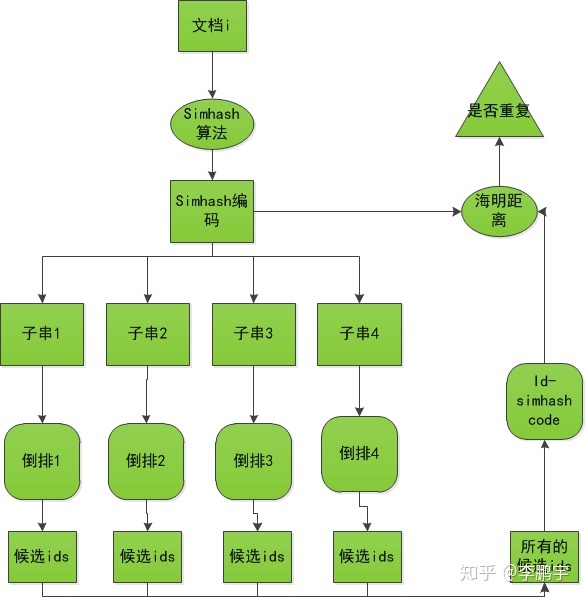
图 4-3 查询的过程

4.5 文本去重框架的 python 实现

github 地址是:

https://github.com/lipengyuer/DataScience/blob/master/src/nlp/LSH/NearRedupRemove.pygithub.com

5 结语

Simhash 的背后是局部敏感哈希；基于 simhash 的文本去重技术背后，是基于局部敏感哈希的海量数据检索技术。

simhash 也可以看做是一种文本你的分布式表示方法。难得的是，这种方法是无监督的。当然了，simhash 挖掘文本信息的能力没有 word2vec 这种模型强，simhash 编码会限制分类、聚类模型的效果上限。一般来说，在低精度、高速度的场景下，可以试一下 simhash。

这里对局部敏感哈希的理解方式，具有较强的个人风格，不一定适合所有的人。如果看不懂，那是我的表达方式导致的。可以参考这里的知识地图搜索套路，整理出属于自己的表达。

注意：本文为李鹏宇 (知乎个人主页https://www.zhihu.com/people/py-li-34) 原创作品，受到著作权相关法规的保护。如需引用、转载，请注明来源信息：（1）作者名，即 “李鹏宇”；（2）原始网页链接，即当前页面地址。如有疑问，可发邮件至我的邮箱:lipengyuer@126.com。
https://zhuanlan.zhihu.com/p/92155250