jump consistent hash的逻辑详解 - 知乎

前言

jump consistent hash 是由谷歌的 John Lamping 和 Eric Veach 发明的一致性哈希算法，这个算法的牛逼之处在于，相比传统的环形一致性哈希，空间复杂度更低，根本无内存占用，而且算法非常简洁，C++ 的实现不到 10 行代码就可以搞定。

算法的原始论文见这个地址《A Fast, Minimal Memory, Consistent Hash Algorithm》。笔者在学习此论文的时候，发现论文中将算法从 O(N)优化到 O(logN)的环节，其推理过程缺失一个环节，导致理解这个算法存在困难（这似乎是大神写论文的一个通病，大神往往在论文中省去某些 “不难证明” 的东西，导致普通人要花费很多精力才能彻底理解）。网上有很多介绍这个算法的文章，基本都和论文的思路类似，也存在相同的问题。

本文会从另外一个角度，一步一步更严谨地证明这个算法。本文适合那些在看原始论文中，对算法由 O(N) 优化到 O(logN) 的过程存在疑问的读者。另外，如果你能从两个不同的角度去理解一个结论，那么你对这个结论的理解将会更加深刻，因此本文也适合那些想加深对jump consistent hash 的理解的读者。

本文大纲

本文会比较长，但其实整个逻辑过程并不复杂，因此先梳理一下本文的大纲。这个大纲是本文的逻辑骨架，整篇文章是在这个逻辑骨架上加血加肉。

本文的大纲很简单，分 3 部分：

• 第 1 部分，介绍一致性哈希的两个重要特点：“一致性” 和 “均匀性”
• 第 2 部分，构造出一个哈希算法，满足 “一致性”，但还不满足 “均匀性”
• 第 3 部分，调整算法中的参数，让其满足 “均匀性”

当然，这个算法在实际应用时不是 100% 完美的，也会存在一些缺点，在文章的最后会简单介绍其缺点和解决方法。

Ⅰ. 一致性哈希的特点

在《A Fast, Minimal Memory, Consistent Hash Algorithm》这篇论文中，作者提出，一致性哈希最重要的两个特性是 “一致性” 和“均匀性”。

1.1 一致性

当给哈希增加一个新桶时，需要对已有的 key 进行重新映射。一致性的意思是，在这个重新映射的过程中，key 要么保留在原来的桶中，要么移动到新增加的桶中。如果 key 移动到原有的其他桶中，就不满足 “一致性” 了。

这是一致性哈希区别于传统哈希的特征，传统的哈希在增加一个新桶时，一般会对 key 进行随机重新的随机映射，key 很可能移动到其他原有的桶中。

1.2 均匀性

均匀性是指 key 会等概率地映射到每个桶中，不会出现某个桶里有大量 key，某个桶里 key 很少甚至没有 key 的情况。

这是一致性哈希和传统哈希都有的特征。

1.3 举例

理解 “一致性” 和“均匀性”是理解后文的基础，这里举几个例子来加深理解：

• 满足 “一致性”，不满足“均匀性” 的哈希

例 1：增加桶 4 后，所有 key 仍保留在原有桶中，满足一致性；但桶中的 key 分部不均匀，不满足均匀性

例 2：增加桶 4 后，所有 key 移动到新桶中，满足一致性；但桶中的 key 分部不均匀，不满足均匀性

例 3：增加桶 4 后，原有桶 1 中的 key 保持不变，桶 2 和桶 3 中的元素移动到新桶中，满足一致性；但桶中的 key 分部不均匀，不满足均匀性

• 不满足 “一致性”，满足“均匀性” 的哈希

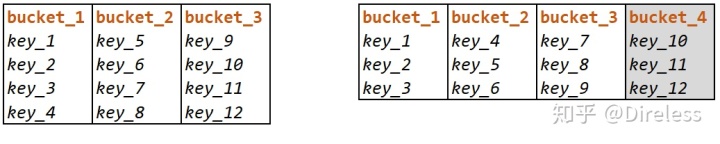
例 4：增加桶 4 后，各 key 均匀分布，满足均匀性；但 key_4 从原有的桶 1 移动到桶 2，不满足一致性

• 同时满足 “一致性” 和“均匀性”的哈希

例 5：增加桶后，各 key 均匀分布，满足均匀性；并且 key 没有在原有的桶中移动，也满足一致性

如果一个哈希算法同时满足 “一致性” 和“均匀性”，那么这个算法就是我们想要的一致性哈希。在本文接下来的两部分里，我们会先构造一个满足 “一致性” 的算法，然后对其进行调整，使其满足“均匀性”，这样我们就可以得到一致性哈希的算法。

Ⅱ. 构造满足一致性，但不满足均匀性的哈希算法

我们先看看 “一致性” 的要求：当增加新桶时，原有桶中的 key 要么保留在原有的桶中，要么移动到新增的这个桶中。

假设一致性哈希函数为
，其中
为要放入元素的键值，
为桶的个数，函数返回值是给
分配的桶
（从 0 开始），返回值的范围为
。那么根据 “一致性” 的要求，有如下的递推公式：

有了这个递推公式，我们就很方便实现满足 “一致性” 的哈希算法了。

2.1 方法 1

直接使用这个递推公式。开始桶的总数为 1，所有的 key 都放在第 0 个桶中。然后每增加一个桶，生成一个随机数，当这个随机数为奇数时，将 key 放在保持在原始桶中，当这个 key 为偶数时，将 key 移动到新增的桶中。

具体 C++ 代码如下：

unsigned int ch(unsigned int key, unsigned int n)
{
    srand(key);
    unsigned int id = 0; // 桶数为1时，所有key放到第0个桶中
    for (unsigned int i = 1; i < n; i++)
    {
        // 每增加一个桶，生成一个随机数
        if (rand() % 2 == 1)
        {
            id = id; // 如果随机数为奇数，key仍然保留在原来的桶中
        }
        else
        {
            id = i; // 如果随机数为偶数，将key移动到新分配的桶中
        }
    }
    return id;
}

注意，由于使用 key 作为随机数的种子，因此一旦 key 和 n 确定了，函数的返回值也就是确定的。并且当函数参数为 n 和参数为 n-1 时，循环过程中的前面几步生成的随机数都是一样的。

2.2 方法 2

开始桶的总数为 1，所有的 key 都放在第 0 个桶中，同时生成一个大于当前桶数的随机数。每增加一个新桶时，判断当前桶总数是否超过这个随机数。如果未超过（桶数小于或等于这个随机数），则将 key 保留在原来的桶中；如超过，则将 key 移动到新增加的桶中，同时重新生成一个大于当前桶数的随机数，后续增加新桶时，使用和前面相同的逻辑进行判断。

和方法 1 一样，我们也使用 key 作为随机数的种子，因此一旦 key 和 n 确定了，函数的返回值也就是确定的。

具体 C++ 代码如下：

unsigned int ch(unsigned int key, unsigned int n)
{
    srand(key);
    unsigned int id = 0;
    unsigned int fence = rand();
    while (n > fence)
    {
        id = fence;
        fence = id + rand();
    }
    return id;
}

这个代码初看可能不太直观，我们一步一步来分析：

• 当 n=1 时，可以看出函数的返回值 id 是 0，同时假设生成一个随机数 fence=3
• 当 n=2, 3 时，因为随机数种子不变，所以开始生成的随机数 fence 也是 3，这个时候函数的返回值 id 仍然是 0
• 当 n=4 时，因为因为随机数种子不变，开始 fence=3，所以 n>fence，进入循环中。进入循环后 id=3，并假设生成的新 fence=3+5=8。此时 n < 新生成的 fence，跳出循环返回 id=3
• 当 n=5, 6, 7, 8 时，因为因为随机数种子不变，开始 fence=3，所以 n>fence，进入循环中。进入循环后 id=3，新生成的 fence=8。此时 n = 新生成的 fence，跳出循环返回 id=3
• 当 n=9 时，前面都是重复 n=5, 6, 7, 8 的步骤。在最后一步时，因为 n=9，fence=8，满足 n>fence，会再次进入循环，此时 id=8，假设新生成fence=8+2=10。此时会跳出循环返回 id=8
• ……

可以看出，这个方法也是满足递推公式的。当输入参数为 n 时，函数的返回值只有两个分支：要么和参数为 n-1 时相同，要么函数的返回值是 n-1。而这两个方法，正好对应论文《A Fast, Minimal Memory, Consistent Hash Algorithm》中 O(N) 和 O(logN) 的两个算法，区别仅在于生成随机数的方式、函数返回值走那个分支的判断方法。

2.3 方法 1 和方法 2 都不满足 “均匀性”

接下来我们分析下这两个方法是否满足 “均匀性”。哈希的“均匀性” 要求对于任意的 key，当桶数为 n 时，key 被分配到任意桶中的概率都是 1/n。

对于方法 1，我们分析下当桶的总数为 3 时，key 被分配到第 0 个桶中的概率：

当桶数为 3 时，循环会执行 2 次，如果要 key 被分配到第 0 个桶，要求两次生成的随机数都是奇数，其概率是 1/4。很明显不满足 “均匀性”

对于方法 2，我们分析下当桶的总数为 2 时，key 被分配到第 0 个桶中的概率：

当桶的总数为 2 时，如果生成的随机数 fence 大于或等于 2，那么不会进入循环体，key 也就被分配到第 0 个桶中了。因为 rand() 的返回值均匀分布在[0, RAND_MAX]之间，因此生成的随机数 fence 大于或等于 2 的概率是非常大的，几乎接近 1。因此这个情况下 key 被分配到第 0 个桶中的概率接近 1。也不满足 “均匀性”。

Ⅲ. 调整算法中的参数，使其满足等均匀性

这部分，我们并不去推导如何设计算法中参数，使满足均匀性。而是直接使用论文中的参数，并证明这个参数能满足均匀性。也就是说，本部分不讲推导过程，仅讲证明过程。

哈希的 “均匀性” 要求对于任意的 key，当桶数为 n 时，key 被分配到任意桶中的概率都是 1/n。

3.1 让方法 1 满足均匀性

先回顾下方法 1 的思路。

方法 1：直接使用这个递推公式。开始桶的总数为 1，所有的 key 都放在第 0 个桶中。然后每增加一个桶，生成一个随机数，当这个随机数为奇数时，将 key 放在保持在原始桶中，当这个 key 为偶数时，将 key 移动到新增的桶中

根据前面的分析，由于增加桶时，key 移动到新桶和保留在原始桶中的概率是 1/2，因此不满足 “均匀性”。那为了让其满足 “均匀性”，我们需要调整 key 移动到新桶和保留在原始桶中的概率。

假设当前桶数为 k，如果新增加一个桶，key 移动到新桶的概率为 1/(k+1)，那么算法就可以满足 “均匀性” 了。我们可以一步一步进行证明：

首先对 n=1、2、3 这个特殊情况进行推导：

• 首先，当桶总数 n=1 时，key 分配到第 0 个桶中的概率是 1
• 新增一个桶，此时 n=2，key 被分配到新桶（第 1 个桶）中的概率是 1/2，保留在原桶中的概率也是 1/2
• 再新增一个桶，此时 n=3，key 被分配到新桶（第 2 个桶）中的概率是 1/3，保留原桶（第 0 或 1 个桶）中的概率是 1/2 * 2/3 = 1/3

然后我们可以有更通用的推导：

• 当 n=k 时，key 被分配到每个桶中的概率是 1/n
• 再新增一个桶，此时 n=k+1，key 被分配到新桶（第 k 个桶）中的概率是 1/(k+1)，保留原桶（第 0 或 1 或…… 或 k-1 个桶）中的概率是 1/k * k/(k+1) = 1/(k+1)。此时 key 被分配到每个桶的概率仍然为 1/n

因此方法 1 的代码修改如下：

int ch(int key, int n)
{
    random.seed(key);
    int id = 0;
    for (int j = 1; j < n; j++)
    {
        if (random.next() < 1.0/(j+1))
        {
            id = j;
        }
    }
    return id;
}

3.2 让方法 2 满足均匀性

先回顾下方法 2 的思路

方法 2：开始桶的总数为 1，所有的 key 都放在第 0 个桶中，同时生成一个大于当前桶数的随机数。每增加一个新桶时，判断当前桶总数是否超过这个随机数。如果未超过（桶数小于或等于这个随机数），则将 key 保留在原来的桶中；如超过，则将 key 移动到新增加的桶中，同时重新生成一个大于当前桶数的随机数，后续增加新桶时，使用和前面相同的逻辑进行判断。

让方法 2 满足 “均匀性” 的关键是如何生成这个随机数。我们在前一部分已分析，如果直接使用
函数来生成其中随机数，将不满足 “均匀性”。

论文中生成这个随机数方法是：假设上一次
跳变的桶
是
，也就是有
，那么生成的随机数
，其中
是
范围内的均匀的随机浮点数，由这个随机数
按照方法 2 中的思路，来决定接下当桶数增加时，
留在原桶还是移动到新桶中。

接下来我们证明为何这样生成随机数，可以保证算法满足 “均匀性”。根据前面的经验，如果我们能证明，当
且
时，有如下结论，那么这个算法将满足 “均匀性”。

为了证明结论 1，我们先设置两个命题：

我们可以证明命题 a和命题 b是等价的：

我们可以证明，命题 b的概率是
：

由于命题 b和命题 a等价，因此命题 a的概率也是
，因此结论 1 成立。

为了证明结论 2，我们在命题 a的基础上，再设置两个命题：

我们可以证明，（命题 a且命题 c）和命题 d是等价的：

我们可以证明命题 d的概率是
（见上面命题 b概率的证明），同时已知命题 a的概率是是
，因此命题 c的概率是
。因此结论 2 成立。

用类似的方法，也可以证明：

因此方法 2也是满足 “均匀性”。方法 2 的最终代码如下：

int ch(int key, int n)
{
    random.seed(key);
    int b = 0;
    int f = 0;
    while (f < n)
    {
        b = f;
        r = random.next();
        f = floor((b+1)/r)
    }
    return b;
}

总结

本文从另外一个角度来解释了 jump consistent hash，希望能够帮助大家理解这个很厉害的算法。

另外，在最后也提一下 jump consistent hash 在实际使用中的缺点和解决方案。和传统的环形一致性哈希相比，这个算法有两个缺点：

1. 不支持设置哈希桶的权重
2. 仅能在末尾增加和删除桶，不能删除中间的哈希桶

我们可以采用计算机科学最传统的方法（增加一个中间层）来解决这两个问题：增加一层虚拟桶，使用 jump consistent hash 来将
分配到虚拟桶中，然后在虚拟桶和实际桶之间建立一个映射关系。这样我们就可以通过映射关系来设置实际桶的权重；也可以在任意位置删除和添加实际桶，只需要维护好映射关系即可。当然，这样做的代价就是，算法本来可以的无内存占用的，现在需要有一块内存来维护映射关系了。
https://zhuanlan.zhihu.com/p/104124045