1.DFS
| 题目 | 难度 | 推荐指数 |
|---|---|---|
| 17. 电话号码的字母组合 | 中等 | dfs+回溯 |
| 22. 括号生成 | 中等 | |
| 37. 解数独 | 困难 | |
| 39. 组合总和 | 中等 | |
| 40. 组合总和 II | 中等 | |
| 211. 添加与搜索单词 - 数据结构设计 | 中等 | |
| 282. 给表达式添加运算符 | 困难 | |
| 301. 删除无效的括号 | 困难 | |
| 341. 扁平化嵌套列表迭代器 | 中等 | |
| 397. 整数替换 | 中等 | |
| 403. 青蛙过河 | 困难 | |
| 437. 路径总和 III | 中等 | |
| 488. 祖玛游戏 | 困难 | |
| 494. 目标和 | 中等 | |
| 559. N 叉树的最大深度 | 简单 | |
| 563. 二叉树的坡度 | 简单 | |
| 589. N 叉树的前序遍历 | 简单 | |
| 590. N 叉树的后序遍历 | 简单 | |
| 606. 根据二叉树创建字符串 | 简单 | |
| 638. 大礼包 | 中等 | |
| 653. 两数之和 IV - 输入 BST | 简单 | |
| 677. 键值映射 | 中等 | |
| 690. 员工的重要性 | 简单 | |
| 778. 水位上升的泳池中游泳 | 困难 | |
| 783. 二叉搜索树节点最小距离 | 简单 | |
| 869. 重新排序得到 2 的幂 | 中等 | |
| 872. 叶子相似的树 | 简单 | |
| 938. 二叉搜索树的范围和 | 简单 | |
| 987. 二叉树的垂序遍历 | 困难 | |
| 993. 二叉树的堂兄弟节点 | 简单 | |
| 1239. 串联字符串的最大长度 | 中等 | |
| 1609. 奇偶树 | 中等 | |
| 1723. 完成所有工作的最短时间 | 困难 | |
| 1766. 互质树 | 困难 | 1766.互质树 |
| 2044. 统计按位或能得到最大值的子集数目 | 困难 | 位运算+状态压缩/回溯 |
2.回溯
| 题目 | 难度 | 推荐指数 |
|---|---|---|
| 17. 电话号码的字母组合 | 中等 | dfs+回溯 |
| 37. 解数独 | 困难 | |
| 39. 组合总和 | 中等 | |
| 40. 组合总和 II | 中等 | |
| 90. 子集 II | 中等 | |
| 131. 分割回文串 | 中等 | |
| 212. 单词搜索 II | 困难 | |
| 301. 删除无效的括号 | 困难 | |
| 306. 累加数 | 中等 | |
| 797. 所有可能的路径 | 中等 | |
| 1219. 黄金矿工 | 中等 | |
| 剑指 Offer 38. 字符串的排列 | 中等 |
3.动态规划
3.1 记忆化搜索
| 题目 | 难度 | 推荐指数 |
|---|---|---|
| 87. 扰乱字符串 | 困难 | 不会写 |
| 375. 猜数字大小 II | 中等 | 注意推导出dp方程,并且需要逆向遍历 for(int i=n-1;i>=1;i—){ for(int j=i+1;j<=n;j++{ }} |
| 403. 青蛙过河 | 困难 | |
| 494. 目标和 | 中等 | |
| 552. 学生出勤记录 II | 困难 | |
| 576. 出界的路径数 | 中等 | |
| 913. 猫和老鼠 | 困难 | |
| 1137. 第 N 个泰波那契数 | 简单 | |
| 剑指 Offer 10- I. 斐波那契数列 | 简单 |
4.状态压缩
| 题目 | 难度 | 推荐指数 |
|---|---|---|
464. 我能赢吗
| 中等 | 464 我能赢吗
状态压缩,枚举所有可能,注意用map存下访问过的状态 |
|
473. 火柴拼正方形
| 中等 | 将正方形分成四个数组,每个数组如果值小于边就加上去,最后用dfs+回溯来求解问题的。(在回溯中间如果dfs得到true,就会直接返回得到true的结果。) | |
698. 划分为k个相等的子集
| 中等 | 698. 划分为k个相等的子集
回溯dfs会超时,需要剪枝(怎么剪枝),此外本题目还可以DP |
5.前缀和
| 题目 | 难度 | 推荐指数 |
|---|---|---|
661. 图片平滑器
| 简单 | 可以使用二维的前缀和来求解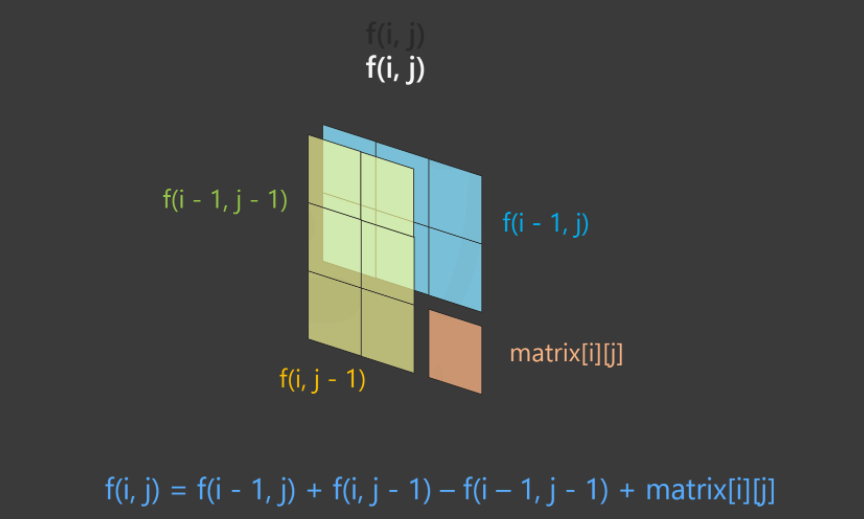 |
|
6.手撕排序算法
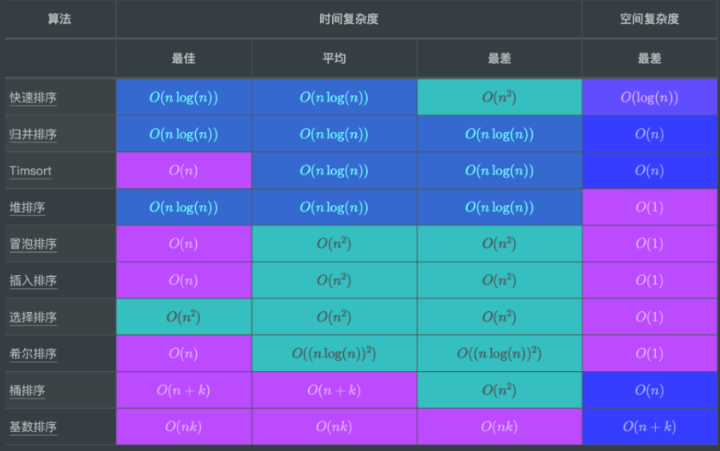
#include <bits/stdc++.h>using namespace std;/*1.冒泡排序稳定排序最佳时间复杂度为o(n)平均时间复杂度为o(n^2)最差时间复杂度为o(n^2)空间复杂度为o(1)*///原版本void bubbleSort(vector<int> &nums){int len = nums.size();for (int i = 0; i < len - 1; ++i){for (int j = 0; j < len - 1 - i; ++J){if (nums[j] > nums[j + 1]){swap(nums[j], nums[j + 1]);}}}}//冒泡优化版本void bubbleSort(vector<int> &nums){int len = nums.size();bool flag = false;for (int i = 0; i < len - 1; ++i){for (int j = 0; j < len - 1 - i; ++J){if (nums[j] > nums[j + 1]){flag = true;swap(nums[j], nums[j + 1]);}}if (flag == false)break;}}/*2.选择排序选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给>二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。不稳定排序最佳时间复杂度为o(n^2)平均时间复杂度为o(n^2)最差时间复杂度为o(n^2)空间复杂度为o(1)*/void selection(vector<int> &a, int n){int minIndex;for (int i = 0; i < n; ++i){minIndex = i;for (int j = i + 1; j < n; ++j){if (a[j] < a[minIndex])minIndex = j;}swap(a[i], a[minIndex]);}}/*3.插入排序插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开 始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面稳定排序最佳时间复杂度为o(n)平均时间复杂度为o(n^2)最差时间复杂度为o(n^2)空间复杂度为o(1)*/void insertionSort(vector<int> &a, int n){ //{ 9,1,5,6,2,3 }for (int i = 1; i < n; ++i){if (a[i] < a[i - 1]){ //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入int j = i - 1;int x = a[i]; //复制为哨兵,即存储待排序元素// a[i] = a[i - 1];//先后移一个元素,可以不要这一句,跟循环里面的功能重复了while (j >= 0 && x < a[j]){ //查找在有序表的插入位置,还必须要保证j是>=0的因为a[j] 要合法a[j + 1] = a[j];j--; //元素后移}a[j + 1] = x; //插入到正确位置}}}/*4.快速排序选取第一个数为基准将比基准小的数交换到前面,比基准大的数交换到后面对左右区间重复第二步,直到各区间只有一个数稳定排序最佳时间复杂度为o(nlogn)平均时间复杂度为o(nlogn)最差时间复杂度为o(n^2)空间复杂度为o(1ogn)*/void quickSort(vector<int> &a, int low, int high){if (low >= high) // 结束标志return;int first = low; // 低位下标int last = high; // 高位下标int key = a[first]; // 设第一个为基准while (first < last){// 从后往前走,将比第一个小的移到前面while (first < last && a[last] > key)last--;if (first < last)a[first++] = a[last];//从前往后走, 将比第一个大的移到后面while (first < last && a[first] <= key)first++;if (first < last)a[last--] = a[first];}a[first] = key;// 前半递归quickSort(a, low, first - 1);// 后半递归quickSort(a, first + 1, high);}/*5.希尔排序希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序希尔排序的思想是采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。稳定排序最佳时间复杂度为o(n)平均时间复杂度为o((nlogn)^2)最差时间复杂度为o((nlogn)^2)空间复杂度为o(1)*/void shellSortCore(vector<int> &nums, int gap, int i){int inserted = nums[i];int j;// 插入的时候按组进行插入for (j = i - gap; j >= 0 && inserted < nums[j]; j -= gap){nums[j + gap] = nums[j];}nums[j + gap] = inserted;}void shellSort(vector<int> &nums){int len = nums.size();//进行分组,最开始的时候,gap为数组长度一半for (int gap = len / 2; gap > 0; gap /= 2){//对各个分组进行插入分组for (int i = gap; i < len; ++i){//将nums[i]插入到所在分组正确的位置上shellSortCore(nums, gap, i);}}for (auto a : nums){cout << a << "";}}/*6.归并排序将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了,之后再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 …直到全部小的数组合并起来。1、把长度为n的输入序列分成两个长度为n/2的子序列;2、对这两个子序列分别采用归并排序;3、 将两个排序好的子序列合并成一个最终的排序序列稳定排序最佳时间复杂度为o(nlogn)平均时间复杂度为o(nlogn)最差时间复杂度为o(nlogn)空间复杂度为o(n)*/void mergeSort(vector<int> &data){int len = data.size();vector<int> dataTemp(len, 0);for (int seg = 1; seg < len; seg += seg){for (int start = 0; start < len; start += seg + seg){int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);int index = low, start1 = low, end1 = mid, start2 = mid, end2 = high;while (start1 < end1 && start2 < end2){dataTemp[index++] = data[start1] < data[start2] ? data[start1++] : data[start2++];}while (start1 < end1){dataTemp[index++] = data[start1++];}while (start2 < end2){dataTemp[index++] = data[start2++];}}swap(data, dataTemp);}for (auto a : data)cout << a << " ";}/*7.堆排序稳定排序最佳时间复杂度为o(nlogn)平均时间复杂度为o(nlogn)最差时间复杂度为o(nlogn)空间复杂度为o(1)*/void heapify(vector<int> &nums, int n, int i) //对有一定顺序的堆,//当前第i个结点取根左右的最大值(这个操作称heapfiy){int l = i * 2 + 1, r = i * 2 + 2;int max = i;if (l < n && nums[l] > nums[max])max = l;if (r < n && nums[r] > nums[max])max = r;if (max != i){swap(nums[max], nums[i]);heapify(nums, n, max);}}void heapify_build(vector<int> &nums, int n) //建立大根堆,从树的倒数第二层第一个结点开始,//对每个结点进行heapify操作,然后向上走{int temp = (n - 2) / 2;for (int i = temp; i >= 0; i--)heapify(nums, n, i);for (int i = 0; i < nums.size(); i++)cout << nums[i] << " ";cout << endl;}void heapify_sort(vector<int> &nums, int n) //建立大根堆之后,每次交换最后一个结点和根节点(最大值),//对交换后的根节点继续进行heapify(此时堆的最后一位是最大值,因此不用管他,n变为n-1){heapify_build(nums, n);for (int i = 0; i < n; i++){swap(nums.front(), nums[n - i - 1]);heapify(nums, n - i - 1, 0);}}/*8.计数排序 Timesort计数排序统计小于等于该元素值的元素的个数i,于是该元素就放在目标数组的索引i位(i≥0)。计数排序基于一个假设,待排序数列的所有数均为整数,且出现在(0,k)的区间之内。如果 k(待排数组的最大值) 过大则会引起较大的空间复杂度,一般是用来排序 0 到 100 之间的数字的最好的算法,但是它不适合按字母顺序排序人名。计数排序不是比较排序,排序的速度快于任何比较排序算法。算法思想:1. 找出待排序的数组中最大和最小的元素;2. 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项;3. 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加);4. 向填充目标数组:将每个元素 i 放在新数组的第 C[i] 项,每放一个元素就将 C[i] 减去 1;稳定排序最佳时间复杂度为o(n)平均时间复杂度为o(nlogn)最差时间复杂度为o(nlogn)空间复杂度为o(n+k)*/#include <iostream>#include <vector>#include <algorithm>using namespace std;// 计数排序void CountSort(vector<int> &vecRaw, vector<int> &vecObj){// 确保待排序容器非空if (vecRaw.size() == 0)return;// 使用 vecRaw 的最大值 + 1 作为计数容器 countVec 的大小int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1;vector<int> vecCount(vecCountLength, 0);// 统计每个键值出现的次数for (int i = 0; i < vecRaw.size(); i++)vecCount[vecRaw[i]]++;// 后面的键值出现的位置为前面所有键值出现的次数之和for (int i = 1; i < vecCountLength; i++)vecCount[i] += vecCount[i - 1];// 将键值放到目标位置for (int i = vecRaw.size(); i > 0; i--) // 此处逆序是为了保持相同键值的稳定性vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1];}int main(){vector<int> vecRaw = {0, 5, 7, 9, 6, 3, 4, 5, 2, 8, 6, 9, 2, 1};vector<int> vecObj(vecRaw.size(), 0);CountSort(vecRaw, vecObj);for (int i = 0; i < vecObj.size(); ++i)cout << vecObj[i] << " ";cout << endl;return 0;}/*9.桶排序将值为i的元素放入i号桶,最后依次把桶里的元素倒出来。算法思想:1. 设置一个定量的数组当作空桶子。2. 寻访序列,并且把项目一个一个放到对应的桶子去。3. 对每个不是空的桶子进行排序。4. 从不是空的桶子里把项目再放回原来的序列中。最佳时间复杂度为o(n+k)平均时间复杂度为o(n+k)最差时间复杂度为o(n^2)空间复杂度为o(n+k)*/function bucketSort(arr, bucketSize){if (arr.length == = 0){return arr;}var i;var minValue = arr[0];var maxValue = arr[0];for (i = 1; i < arr.length; i++){if (arr[i] < minValue){minValue = arr[i]; // 输入数据的最小值}else if (arr[i] > maxValue){maxValue = arr[i]; // 输入数据的最大值}}// 桶的初始化var DEFAULT_BUCKET_SIZE = 5; // 设置桶的默认数量为5bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;var buckets = new Array(bucketCount);for (i = 0; i < buckets.length; i++){buckets[i] = [];}// 利用映射函数将数据分配到各个桶中for (i = 0; i < arr.length; i++){buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);}arr.length = 0;for (i = 0; i < buckets.length; i++){insertionSort(buckets[i]); // 对每个桶进行排序,这里使用了插入排序for (var j = 0; j < buckets[i].length; j++){arr.push(buckets[i][j]);}}return arr;}/*10、基数排序一种多关键字的排序算法,可用桶排序实现。算法思想:1. 取得数组中的最大数,并取得位数;2. arr为原始数组,从最低位开始取每个位组成radix数组;3. 对radix进行计数排序(利用计数排序适用于小范围数的特点)最佳时间复杂度为o(nk)平均时间复杂度为o(nk)最差时间复杂度为o(nk)空间复杂度为o(n+k)*/int maxbit(int data[], int n) //辅助函数,求数据的最大位数{int maxData = data[0]; ///< 最大数/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。for (int i = 1; i < n; ++i){if (maxData < data[i])maxData = data[i];}int d = 1;int p = 10;while (maxData >= p){// p *= 10; // Maybe overflowmaxData /= 10;++d;}return d;/* int d = 1; //保存最大的位数int p = 10;for(int i = 0; i < n; ++i){while(data[i] >= p){p *= 10;++d;}}return d;*/}void radixsort(int data[], int n) //基数排序{int d = maxbit(data, n);int *tmp = new int[n];int *count = new int[10]; //计数器int i, j, k;int radix = 1;for (i = 1; i <= d; i++) //进行d次排序{for (j = 0; j < 10; j++)count[j] = 0; //每次分配前清空计数器for (j = 0; j < n; j++){k = (data[j] / radix) % 10; //统计每个桶中的记录数count[k]++;}for (j = 1; j < 10; j++)count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶for (j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中{k = (data[j] / radix) % 10;tmp[count[k] - 1] = data[j];count[k]--;}for (j = 0; j < n; j++) //将临时数组的内容复制到data中data[j] = tmp[j];radix = radix * 10;}delete[] tmp;delete[] count;}
7.布隆过滤器
布隆过滤器原理与优点
布隆过滤器是一个比特向量或者比特数组,它本质上是一种概率型数据结构,用来查找一个元素是否在
集合中,支持高效插入和查询某条记录。常作为针对超大数据量下高效查找数据的一种方法。
它的具体工作过程是这样子的:
假设布隆过滤器的大小为m(比特向量的长度为m),有k个哈希函数,它对每个数据用这k个哈希函数
计算哈希,得到k个哈希值,然后将向量中相应的位设为1。在查询某个数据是否存在的时候,对这个数
据用k个哈希函数得到k个哈希值,再在比特向量中相应的位查找是否为1,如果某一个相应的位不为1,
那这个数据就肯定不存在。但是如果全找到了,则这个数据有可能存在。
为什么说有可能存在呢?
因为不同的数据经过哈希后可能有相同的哈希值,在比特向量上某个位置查找到1也可能是由于某个另
外的数据映射得到的。
支持删除操作吗
目前布隆过滤器只支持插入和查找操作,不支持删除操作,如果要支持删除,就要另外使用一个计数变
量,每次将相应的位置为1则计数加一,删除则减一。
布隆过滤器中哈希函数的个数需要选择。如果太多则很快所有位都置为1,如果太少会容易误报。

